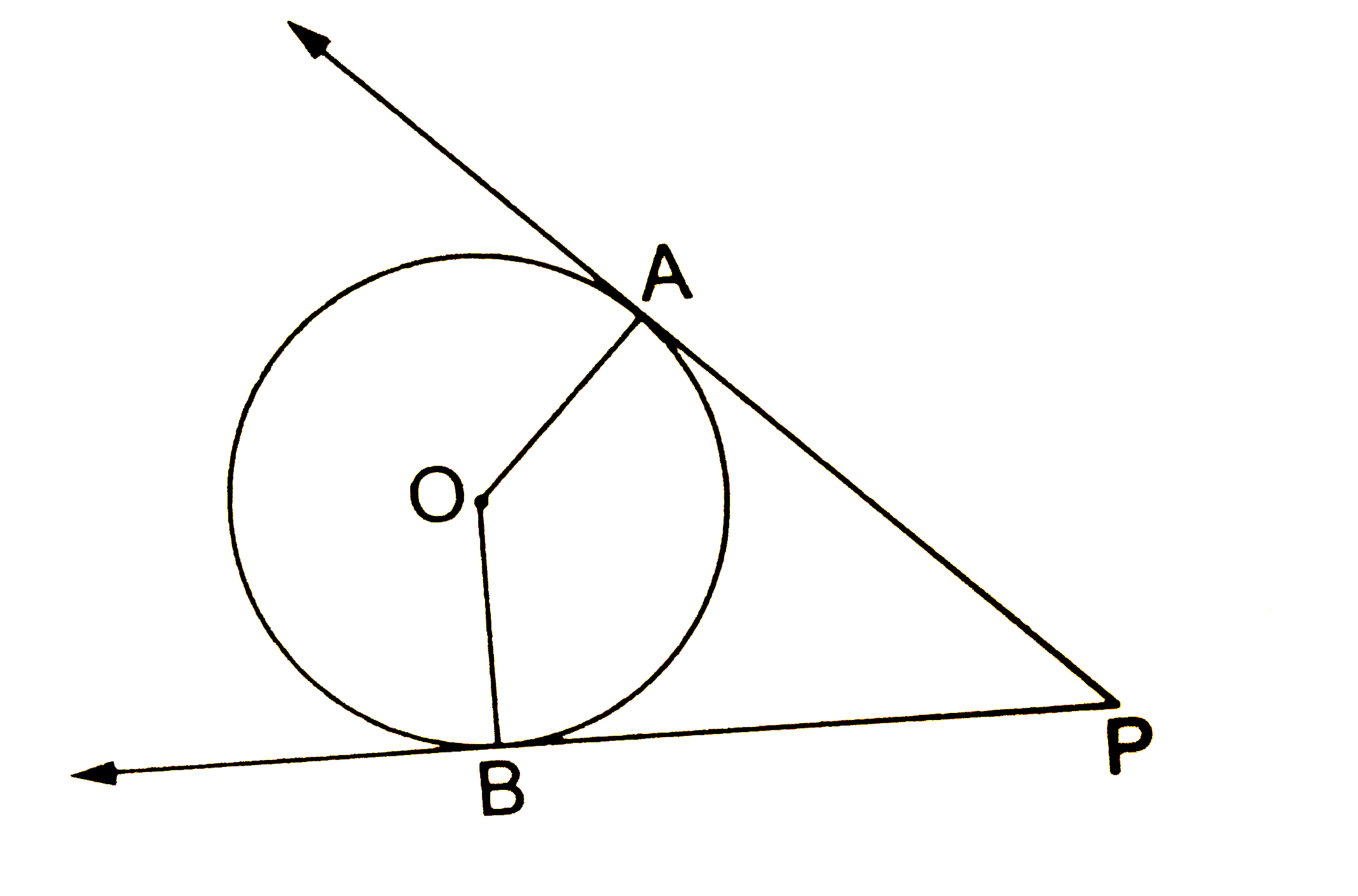
O is the centre on the circle. PA and PB are tangent segments. Then the quadrilateral AOBP is :
Rectangle
Square
Cyclic
None of these
The correct Answer is:C
To solve the problem, we need to analyze the given information about the circle and the tangents. Let's break it down step by step:
1. Identify the Elements:
- Let O be the center of the circle.
- PA and PB are tangent segments from point P to points A and B on the circle.
2. Understanding Tangents:
- By the property of tangents, we know that the tangent to a circle is perpendicular to the radius at the point of tangency.
- Therefore, OA⊥PA and OB⊥PB. This means that ∠OAP=90∘ and ∠OBP=90∘.
3. Analyzing Quadrilateral AOBP:
- The quadrilateral AOBP consists of points A, O, B, and P.
- We have established that ∠OAP=90∘ and ∠OBP=90∘.
4. Sum of Angles in Quadrilateral:
- The sum of the interior angles of any quadrilateral is 360∘.
- Therefore, we can express this as:
∠AOB+∠OBP+∠BPA+∠PAO=360∘
5. Substituting Known Angles:
- We know:
- ∠OBP=90∘
- ∠PAO=90∘
- Substituting these values into the equation:
∠AOB+90∘+∠BPA+90∘=360∘
- Simplifying this gives:
∠AOB+∠BPA+180∘=360∘
- Thus, we have:
∠AOB+∠BPA=180∘
6. Conclusion on Opposite Angles:
- Since the sum of the opposite angles ∠AOB and ∠BPA is 180∘, we can conclude that quadrilateral AOBP is a cyclic quadrilateral.
- In a cyclic quadrilateral, the sum of the opposite angles is always 180∘.
Final Answer:
Therefore, the quadrilateral AOBP is a cyclic quadrilateral.
---
- Let O be the center of the circle.
- PA and PB are tangent segments from point P to points A and B on the circle.
- By the property of tangents, we know that the tangent to a circle is perpendicular to the radius at the point of tangency.
- Therefore, OA⊥PA and OB⊥PB. This means that ∠OAP=90∘ and ∠OBP=90∘.
- The quadrilateral AOBP consists of points A, O, B, and P.
- We have established that ∠OAP=90∘ and ∠OBP=90∘.
- The sum of the interior angles of any quadrilateral is 360∘.
- Therefore, we can express this as:
∠AOB+∠OBP+∠BPA+∠PAO=360∘
- We know:
- ∠OBP=90∘
- ∠PAO=90∘
- Substituting these values into the equation:
∠AOB+90∘+∠BPA+90∘=360∘
- Simplifying this gives:
∠AOB+∠BPA+180∘=360∘
- Thus, we have:
∠AOB+∠BPA=180∘
- Since the sum of the opposite angles ∠AOB and ∠BPA is 180∘, we can conclude that quadrilateral AOBP is a cyclic quadrilateral.
- In a cyclic quadrilateral, the sum of the opposite angles is always 180∘.
Therefore, the quadrilateral AOBP is a cyclic quadrilateral.
Topper's Solved these Questions
Similar Questions
Knowledge Check
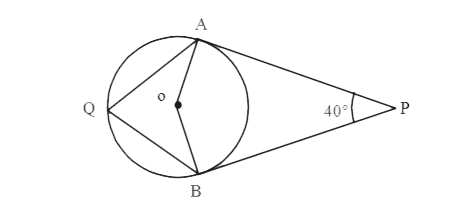
PA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=100∘ , then OAB is equal to:
A25∘B20∘C35∘D50∘PA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=40∘, then ∠OABis equal to:
A40∘B20∘C50∘D25∘
PA and PB are tangents to the circle with centre O from an external point P, touching the circle at A and B respectively. Show that the quadrilateral AOBP is cyclic.
View Solutiongiven below, O in the centre of circle, PA and PB are the pair of tangent drawn to the circel from point P outside the circle. If ∠APB=40∘, then find ∠AOB.

View SolutionIf PAB are secant to the circle and PT is tangent segment; then PA×PB=PT2
View SolutionPoint O is the centre of a circle . Line a and line b are parallel tangents to the circle at P and Q. Prove that segment PQ is a diameter of the circle.

View SolutionPA and PB are the two tangents drawn on a circle from and external point P. The centre of the circle is O and the tangents touches the circles at points A and B. Then quadrilateral OAPB is-
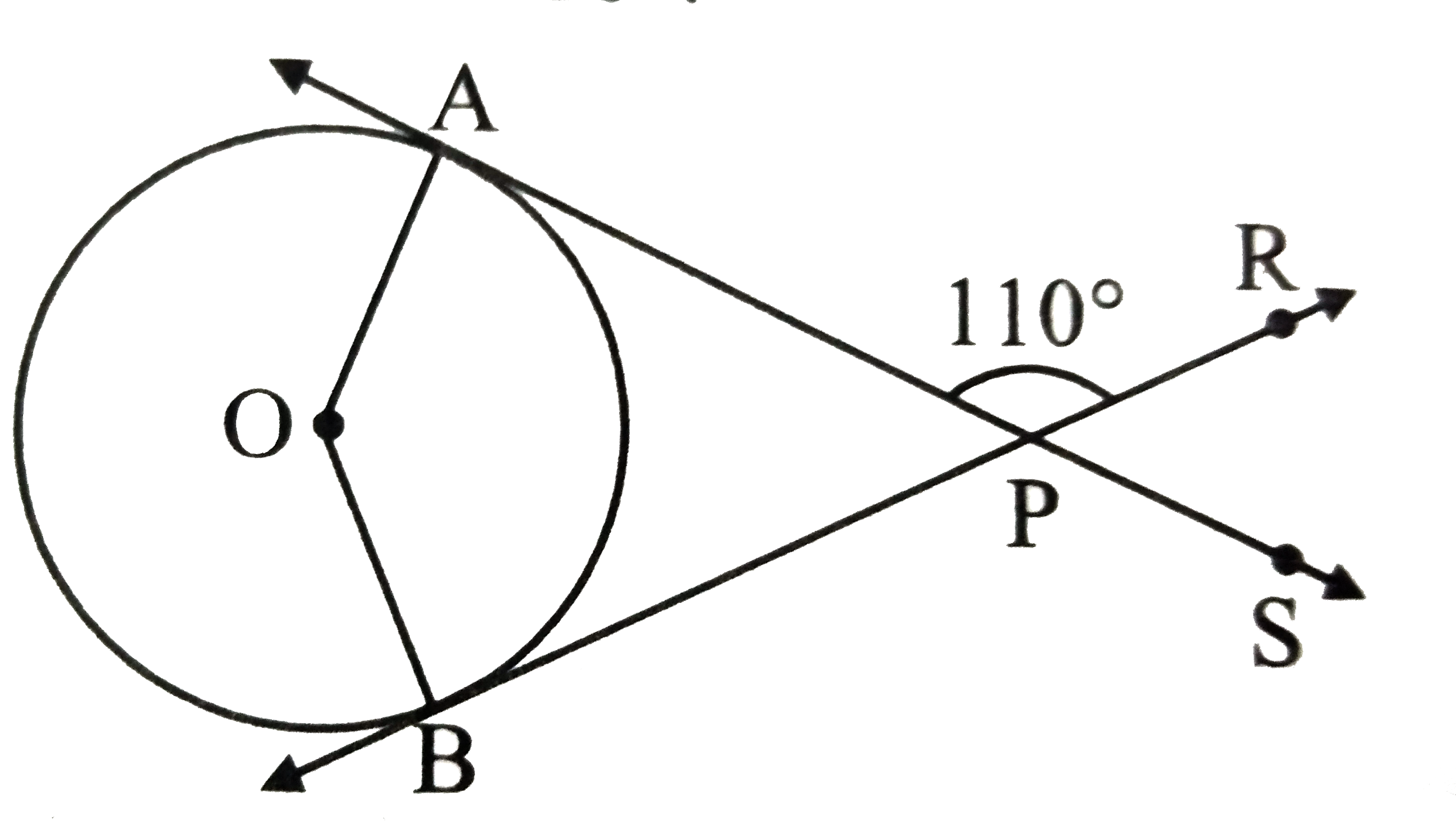
View SolutionFind the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR=110∘
View Solution