BL and CN are the two medians of the ΔABC where ∠A=90∘. If BC=5cm,BL=3√52cm then find the value of CN.
3√5
√5
2√5
5√3
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the triangle and given values
We have triangle ABC with angle A = 90 degrees. The lengths given are:
- BC = 5 cm
- Median BL = (3√5)/2 cm
Step 2: Set up the triangle
Since angle A is 90 degrees, we can use the properties of right triangles. Let:
- AB = 2x
- AC = 2y
- BC = 5 cm (as given)
Step 3: Apply Pythagorean theorem
Using the Pythagorean theorem in triangle ABC:
AB2+AC2=BC2
Substituting the values:
(2x)2+(2y)2=52
This simplifies to:
4x2+4y2=25
Dividing by 4 gives us:
x2+y2=254 (Equation 1)
Step 4: Set up the median
The median BL divides side AC into two equal parts at point L. Therefore, AL = LC = y.
Using the Pythagorean theorem in triangle ABL:
AB2+AL2=BL2
Substituting the values:
(2x)2+y2=(3√52)2
This simplifies to:
4x2+y2=454 (Equation 2)
Step 5: Solve the equations
Now we have two equations:
1. 4x2+4y2=25 (Equation 1)
2. 4x2+y2=454 (Equation 2)
From Equation 1, we can express 4y2:
4y2=25−4x2
Substituting this into Equation 2:
4x2+(25−4x2)=454
This simplifies to:
25=454
Now, we need to solve for x2 and y2.
Step 6: Isolate and solve for x^2
From Equation 1:
4x2+4y2=25
Substituting 4y2:
4x2+25−4x2=454
This leads to:
25−454=0
Calculating gives:
100−45=55
Thus:
4x2=554
So:
x2=5516
Step 7: Find y^2
Substituting x2 back into Equation 1:
4(5516)+4y2=25
This leads to:
554+4y2=25
Solving for y2:
4y2=25−554
4y2=100−554=454
Thus:
y2=4516
Step 8: Find CN
Now we will find CN using the median formula:
In triangle ACN:
AC2+AN2=CN2
Where:
- AC = 2y
- AN = x
Substituting:
(2y)2+x2=CN2
4y2+x2=CN2
Substituting the values:
4(4516)+5516=CN2
This simplifies to:
180+5516=CN2
CN2=23516
Step 9: Calculate CN
Taking the square root:
CN=√23516=√2354
Final Answer
Thus, the value of CN is:
CN=√2354 cm
We have triangle ABC with angle A = 90 degrees. The lengths given are:
- BC = 5 cm
- Median BL = (3√5)/2 cm
Since angle A is 90 degrees, we can use the properties of right triangles. Let:
- AB = 2x
- AC = 2y
- BC = 5 cm (as given)
Using the Pythagorean theorem in triangle ABC:
AB2+AC2=BC2
Substituting the values:
(2x)2+(2y)2=52
This simplifies to:
4x2+4y2=25
Dividing by 4 gives us:
x2+y2=254 (Equation 1)
The median BL divides side AC into two equal parts at point L. Therefore, AL = LC = y.
AB2+AL2=BL2
Substituting the values:
(2x)2+y2=(3√52)2
This simplifies to:
4x2+y2=454 (Equation 2)
Now we have two equations:
1. 4x2+4y2=25 (Equation 1)
2. 4x2+y2=454 (Equation 2)
4y2=25−4x2
4x2+(25−4x2)=454
This simplifies to:
25=454
Now, we need to solve for x2 and y2.
From Equation 1:
4x2+4y2=25
Substituting 4y2:
4x2+25−4x2=454
This leads to:
25−454=0
Calculating gives:
100−45=55
Thus:
4x2=554
So:
x2=5516
Substituting x2 back into Equation 1:
4(5516)+4y2=25
This leads to:
554+4y2=25
Solving for y2:
4y2=25−554
4y2=100−554=454
Thus:
y2=4516
Now we will find CN using the median formula:
In triangle ACN:
AC2+AN2=CN2
Where:
- AC = 2y
- AN = x
(2y)2+x2=CN2
4y2+x2=CN2
Substituting the values:
4(4516)+5516=CN2
This simplifies to:
180+5516=CN2
CN2=23516
Taking the square root:
CN=√23516=√2354
Thus, the value of CN is:
CN=√2354 cm
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a Δ right angled at B . AC = 5 cm , median AL=3√52 find the length of second median CM in cm ?
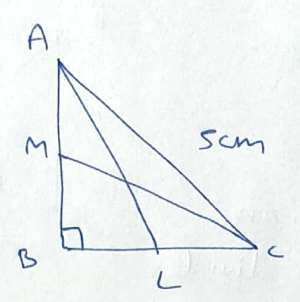 A2√5 cmB5√2 cmC10√2 cmD4√5 cm
A2√5 cmB5√2 cmC10√2 cmD4√5 cmIn figure, ABC is a right triangle, right angled at B. AD and CE are the two medians drawn from A and C respectively. If AC = 5 cm and AD=3√52cm, find the length of CE:
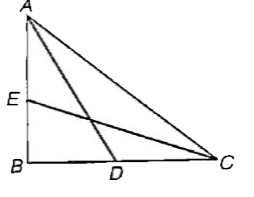 A2√5cmB2.5cmC5cmD4√2cm
A2√5cmB2.5cmC5cmD4√2cmIn figure, ABC is a right triangle, right angled at B. AD and CE are the two medians drawn from A and C respectively. If AC = 5 cm and AD=3√52cm, find the length of CE:
 A2 cmB2√5 cmC5√2 cmD3√2 cm
A2 cmB2√5 cmC5√2 cmD3√2 cm
BL and CM are medians of ΔABC, right - angled a A.
Prove that 4(BL2+CM2)=5 BC2
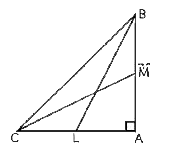
View SolutionBL and CM are medians of a triangle ABC right angled at A. Prove that 4(BL2+CM2)=5BC2
View SolutionABC is a right triangle with ∠B=90∘. If AB = BC = 4√2cm and BM is the median. Then the length of BM is
View SolutionIn ΔABC (in the figure) , ∠B=90∘ , AE=CD=13 cm , BE =AD =5 cm . Then BC=
View SolutionIn ΔABC,∠B is right angle, AB = 5 cm and BC = 12cm , then the value of cosC is :
View Solution
