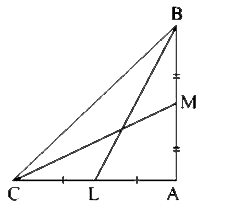
BL and CM are medians of ΔABC, right - angled a A.
Prove that 4(BL2+CM2)=5 BC2
Video Solution
Text Solution
The correct Answer is:4(BL2+CM2)=5 BC2
|
Answer
Step by step video, text & image solution for BL and CM are medians of DeltaABC, right - angled a A. Prove that 4("BL"^(2)+"CM"^(2))=5" BC"^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - PART - B (SECTION - IV)
18 Videos
- SAMPLE PAPER 6BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - SECTION- C
10 Videos
- SAMPLE PAPER 8BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - PART - B (SECTION - V)
4 Videos
Similar Questions
Knowledge Check
In a Δ right angled at B . AC = 5 cm , median AL=3√52 find the length of second median CM in cm ?
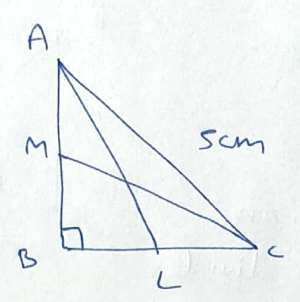 A2√5 cmB5√2 cmC10√2 cmD4√5 cm
A2√5 cmB5√2 cmC10√2 cmD4√5 cmIf ABC is a right angled triangle at B and M, N are the mid-points of AB and BC, then 4(AN2+CM2) is equal to :
A4AC2B5AC2C54AC2D6AC2BL and CN are the two medians of the ΔABC where ∠A=90∘. If BC=5cm,BL=3√52cm then find the value of CN.
A3√5B√5C2√5D5√3
seg AN and seg CM are the medians of △ABC in which ∠B=90∘ Prove that 4(AN2+CM2)=5AC2
View SolutionIn ΔABC,∠C=45∘, prove that AB2+BC2−4A(ΔABC).
View SolutionIn ΔABC , right - angled at B , AB = 24 cm , BC = 7 cm .
sinC,cosC
View SolutionIn right angled ΔBAC,∠BAC=90∘ ,segments AD,BE and CF are medians.Prove that 2(AD2+BE2+CF2)=3BC2
View SolutionIn ΔABC , right - angled at B , AB = 24 cm , BC = 7 cm .
sinA,cosA
View Solution