The solution set of −12<4−3x−5≤2,x∈R is
(103,803]
[−803,103)
(−803,−103]
(803,−103)
The correct Answer is:C
To solve the inequality −12<4−3x−5≤2, we will break it down into steps.
Step 1: Rewrite the inequality
We start with the inequality:
−12<4−3x−5≤2
Step 2: Simplify the inequality
We can rewrite the inequality as two separate inequalities:
1. −12<4−3x−5
2. 4−3x−5≤2
Step 3: Solve the first inequality
For the first inequality:
−12<4−3x−5
Subtract 4 from both sides:
−12−4<−3x−5
This simplifies to:
−16<−3x−5
Multiplying both sides by -5 (remember to flip the inequality sign):
80>3x
or
3x<80
Dividing by 3:
x<803
Step 4: Solve the second inequality
Now for the second inequality:
4−3x−5≤2
Subtract 4 from both sides:
−3x−5≤2−4
This simplifies to:
3x5≤−2
Multiplying both sides by 5:
3x≤−10
Dividing by 3:
x≤−103
Step 5: Combine the results
Now we have two inequalities:
1. x<803
2. x≤−103
Since x must satisfy both conditions, we combine them:
−103≤x<803
Final Answer
Thus, the solution set is:
x∈(−103,803)
We start with the inequality:
−12<4−3x−5≤2
We can rewrite the inequality as two separate inequalities:
1. −12<4−3x−5
2. 4−3x−5≤2
For the first inequality:
−12<4−3x−5
Subtract 4 from both sides:
−12−4<−3x−5
This simplifies to:
−16<−3x−5
Multiplying both sides by -5 (remember to flip the inequality sign):
80>3x
or
3x<80
Dividing by 3:
x<803
Now for the second inequality:
4−3x−5≤2
Subtract 4 from both sides:
−3x−5≤2−4
This simplifies to:
3x5≤−2
Multiplying both sides by 5:
3x≤−10
Dividing by 3:
x≤−103
Now we have two inequalities:
1. x<803
2. x≤−103
−103≤x<803
Thus, the solution set is:
x∈(−103,803)
Topper's Solved these Questions
- LINEAR INEQUALITIES Book:ICSEChapter:LINEAR INEQUALITIES Exercise:MULTIPLE CHOICE QUESTION
Explore 16 Videos
- LIMITS AND DERIVATIVES Book:ICSEChapter:LIMITS AND DERIVATIVES Exercise:Multiple Choice Questions
Explore 31 Videos
- MATHEMATICAL INDUCTIONBook:ICSEChapter:MATHEMATICAL INDUCTIONExercise:Exercise (a)
Explore 1 Video
Similar Questions
Knowledge Check
The solution set of 6≤−3(2x−4)<12,x∈R is
A(0,1]B[1,0)C(0,1)D[0,1]Assertion: The solution set of −1<3+4x≤23,x∈R on the number line is

Reason: In the solution set, the number -1 is not included and the number 5 is included.ABoth assertion and reason are correct and reason is the correct explanation of assertionBBoth assertion and reason are correct but reason is not the correct explanation of assertionCAssertion is correct but reason is incorrectDAssertion is incorrect but reason is correctThe solution set of 2x+13<3x−25x∈R on the number line is
A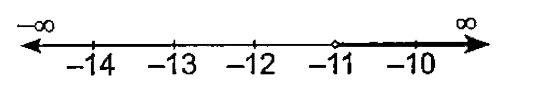 B
B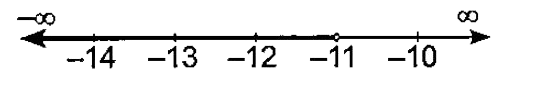 C
C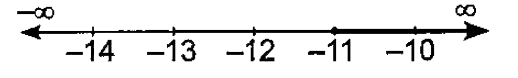 D
D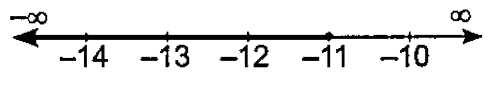
The solution set of x2+2≤3x≤2x2−5, is
View SolutionThe solution set of the inequation 4x+32x−5<6, is
View SolutionThe solution set of −2+10x≤13x+10<24+10x,x∈Z is
View SolutionThe solution set of −1≤3+4x<23,x∈W is
View SolutionThe solution set of 11x−4<15x+4≤13x+14,x∈I, on the number line is
View Solution

