If then
The correct Answer is:B
To solve the inequality x4<5x−23−7x−35, we will follow these steps:
Step 1: Rewrite the inequality
Start with the given inequality:
x4<5x−23−7x−35
Step 2: Find a common denominator
The denominators are 4, 3, and 5. The least common multiple (LCM) of these numbers is 60. We will rewrite each term with a denominator of 60.
Step 3: Rewrite each fraction
- For x4:
x4=15x60
- For 5x−23:
5x−23=20(5x−2)60=100x−4060
- For 7x−35:
7x−35=12(7x−3)60=84x−3660
Step 4: Substitute back into the inequality
Now substitute these back into the inequality:
15x60<100x−4060−84x−3660
Step 5: Combine the fractions on the right
Combine the right-hand side:
100x−40−84x+3660=(100x−84x)+(−40+36)60=16x−460
Step 6: Set up the new inequality
Now we have:
15x60<16x−460
Step 7: Eliminate the denominator
Since the denominators are the same, we can multiply through by 60 (which is positive, so the inequality direction remains the same):
15x<16x−4
Step 8: Rearrange the inequality
Now, rearranging gives:
15x−16x<−4⟹−x<−4
Step 9: Multiply by -1
Multiplying both sides by -1 (remember to flip the inequality):
x>4
Step 10: Write the solution in interval notation
The solution in interval notation is:
(4,∞)
Conclusion
Thus, the solution to the inequality is:
x∈(4,∞)
Start with the given inequality:
x4<5x−23−7x−35
The denominators are 4, 3, and 5. The least common multiple (LCM) of these numbers is 60. We will rewrite each term with a denominator of 60.
- For x4:
x4=15x60
- For 5x−23:
5x−23=20(5x−2)60=100x−4060
- For 7x−35:
7x−35=12(7x−3)60=84x−3660
Now substitute these back into the inequality:
15x60<100x−4060−84x−3660
Combine the right-hand side:
100x−40−84x+3660=(100x−84x)+(−40+36)60=16x−460
Now we have:
15x60<16x−460
Since the denominators are the same, we can multiply through by 60 (which is positive, so the inequality direction remains the same):
15x<16x−4
Now, rearranging gives:
15x−16x<−4⟹−x<−4
Multiplying both sides by -1 (remember to flip the inequality):
x>4
The solution in interval notation is:
(4,∞)
Thus, the solution to the inequality is:
x∈(4,∞)
Topper's Solved these Questions
- LINEAR INEQUALITIES BOOK - ICSECHAPTER - LINEAR INEQUALITIES EXERCISE - MULTIPLE CHOICE QUESTION
16 Videos
- LIMITS AND DERIVATIVES BOOK - ICSECHAPTER - LIMITS AND DERIVATIVES EXERCISE - Multiple Choice Questions
31 Videos
- MATHEMATICAL INDUCTIONBOOK - ICSECHAPTER - MATHEMATICAL INDUCTIONEXERCISE - Exercise (a)
1 Videos
Similar Questions
Knowledge Check
The solution set of 2x+13<3x−25x∈R on the number line is
A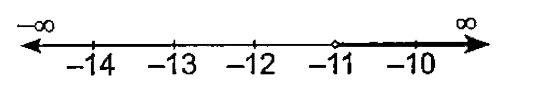 B
B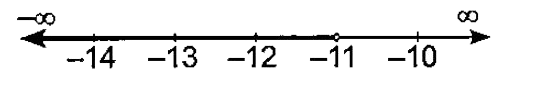 C
C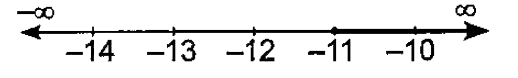 D
D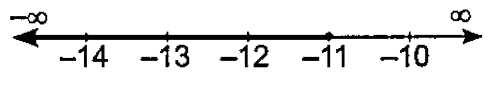
The solution set of 3x5+2<x+4≤x2+5,x∈R on the number line is:
A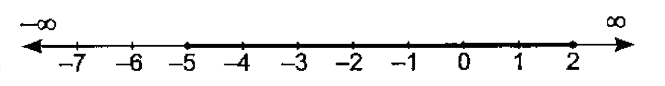 B
B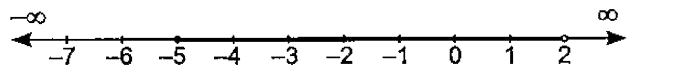 C
C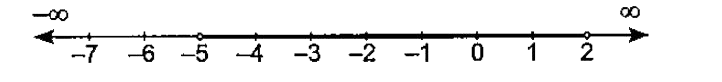 D
D
If −5<2x−3≤x+2,x∈R, then the solution set of x on the number line is
A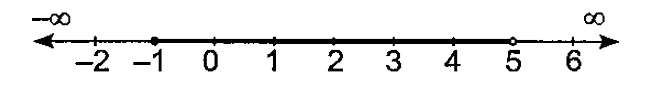 B
B C
C D
D
Let f(x)=mx2+3x+4x2+3x+4,m∈R . If f(x)<5 for all x∈R then the possible set of values of m is :
View SolutionSolve the inequation 3x−7<5x−3 If x ∈ R and represent the solution on the number line
View SolutionSolve the inequalities for real x : x4<(5x−2)3−(7x−3)5
View SolutionSolve the inequalities for real x : x4<(5x−2)3−(7x−3)5
View SolutionIf 2x−3<x+1<4x+7,x∈R then the solution set of x on the number line is:
View Solution
