Calcualte rms value of current and voltages for the giving cases
i) I = 4+3sinωt
ii) V = 5+2cosωt
(iii) i=2+3sinωt=2cosωt
iv) V=cosωt+2cos2ωt
To solve the problem of calculating the RMS (Root Mean Square) values of current and voltage for the given cases, we will follow these steps:
Step 1: Understand the RMS Value Calculation
The RMS value of a constant is the constant itself, and the RMS value of a sinusoidal function can be calculated using the formula:
- For a sine function: Irms=I0√2
- For a cosine function: Vrms=V0√2
Step 2: Calculate RMS for Each Case
Case (i): I=4+3sin(ωt)
1. The constant part is 4.
2. The RMS value of 3sin(ωt) is 3√2.
3. Therefore, the total RMS value is:
Irms=4+3√2
Case (ii): V=5+2cos(ωt)
1. The constant part is 5.
2. The RMS value of 2cos(ωt) is 2√2.
3. Therefore, the total RMS value is:
Vrms=5+2√2
Case (iii): I=2+3sin(ωt)+2cos(ωt)
1. The constant part is 2.
2. The RMS value of 3sin(ωt) is 3√2.
3. The RMS value of 2cos(ωt) is 2√2.
4. Therefore, the total RMS value is:
Irms=2+3√2+2√2=2+5√2
Case (iv): V=cos(ωt)+2cos(2ωt)
1. The RMS value of cos(ωt) is 1√2.
2. The RMS value of 2cos(2ωt) is 2√2.
3. Therefore, the total RMS value is:
Vrms=1√2+2√2=3√2
Final Results
1. For case (i): Irms=4+3√2
2. For case (ii): Vrms=5+2√2
3. For case (iii): Irms=2+5√2
4. For case (iv): Vrms=3√2
The RMS value of a constant is the constant itself, and the RMS value of a sinusoidal function can be calculated using the formula:
- For a sine function: Irms=I0√2
- For a cosine function: Vrms=V0√2
1. The constant part is 4.
2. The RMS value of 3sin(ωt) is 3√2.
3. Therefore, the total RMS value is:
Irms=4+3√2
1. The constant part is 5.
2. The RMS value of 2cos(ωt) is 2√2.
3. Therefore, the total RMS value is:
Vrms=5+2√2
1. The constant part is 2.
2. The RMS value of 3sin(ωt) is 3√2.
3. The RMS value of 2cos(ωt) is 2√2.
4. Therefore, the total RMS value is:
Irms=2+3√2+2√2=2+5√2
1. The RMS value of cos(ωt) is 1√2.
2. The RMS value of 2cos(2ωt) is 2√2.
3. Therefore, the total RMS value is:
Vrms=1√2+2√2=3√2
1. For case (i): Irms=4+3√2
2. For case (ii): Vrms=5+2√2
3. For case (iii): Irms=2+5√2
4. For case (iv): Vrms=3√2
Similar Questions
Knowledge Check
Which of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic motion? Give the period for each case.
(i)sinωt−cosωt (ii) sin2ωt (iii) cosωt+2sin2ωtAa simple harmonic motion with a period πω.Ba simple harmonic motion with a period 2πωCa periodic, but not simple harmonic motionn with a period πωDa periodic, but not simple harmonic motion with a period 2πω
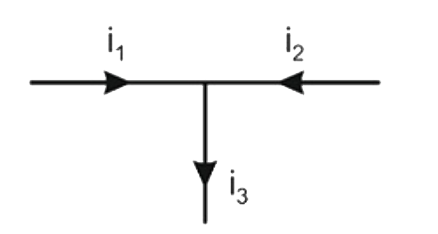
In the given figure, if i1=3sinωtandi2=4cosωt, then i3 is
View Solutionr.m.s. value of current i=3+4sin (omegat+pi//3) is
View SolutionThe electric current in a circuit is given by I = 3 sin ωt+4cosωt. The rms current is
View SolutionFind the rms value of current from t=0 to t=2πω if the current varies as i=Imsinωt.
View SolutionFind the rms value of current from t=0 to t=2πω if the current avries as i=Imsinωt.
View SolutionFind the rms value of current from t=0 to t=2πω if the current avries as i=Imsinωt.
View SolutionWhich of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic motion? Give the period for each case.
(i)sinωt−cosωt (ii) sin2ωt (iii) cosωt+2sin2ωt
View Solution
