Find the average value in the following cases
(i) i=4+3cosωt
(ii) I=5sinωt+2sin2ωt+3sin3ωt
(iv) V=cosωt+3cos2ωt+3cos3ωt+2
To find the average value of the given functions, we will follow the properties of average values of sinusoidal functions and constants. The average value of a function over a complete cycle can be calculated using the following principles:
1. The average value of a constant is the constant itself.
2. The average value of sine and cosine functions over a complete cycle is zero.
Now, let's solve each case step by step.
(i) i=4+3cos(ωt)
Step 1: Identify the constant and the cosine term.
- The constant term is 4.
- The cosine term is 3cos(ωt).
Step 2: Calculate the average value.
- The average of a constant 4 is 4.
- The average of 3cos(ωt) over one complete cycle is 0.
Step 3: Combine the average values.
- Therefore, the average value iavg=4+0=4.
(ii) I=5sin(ωt)+2sin(2ωt)+3sin(3ωt)
Step 1: Identify the sine terms.
- The terms are 5sin(ωt), 2sin(2ωt), and 3sin(3ωt).
Step 2: Calculate the average value of each sine term.
- The average of 5sin(ωt) over one complete cycle is 0.
- The average of 2sin(2ωt) over one complete cycle is 0.
- The average of 3sin(3ωt) over one complete cycle is 0.
Step 3: Combine the average values.
- Therefore, the average value Iavg=0+0+0=0.
(iii) V=cos(ωt)+3cos(2ωt)+3cos(3ωt)+2
Step 1: Identify the constant and cosine terms.
- The constant term is 2.
- The cosine terms are cos(ωt), 3cos(2ωt), and 3cos(3ωt).
Step 2: Calculate the average value of each cosine term.
- The average of cos(ωt) over one complete cycle is 0.
- The average of 3cos(2ωt) over one complete cycle is 0.
- The average of 3cos(3ωt) over one complete cycle is 0.
Step 3: Combine the average values.
- Therefore, the average value Vavg=0+0+0+2=2.
Summary of Results:
- (i) Average value of i=4
- (ii) Average value of I=0
- (iii) Average value of V=2
2. The average value of sine and cosine functions over a complete cycle is zero.
- The constant term is 4.
- The cosine term is 3cos(ωt).
- The average of a constant 4 is 4.
- The average of 3cos(ωt) over one complete cycle is 0.
- Therefore, the average value iavg=4+0=4.
- The terms are 5sin(ωt), 2sin(2ωt), and 3sin(3ωt).
- The average of 5sin(ωt) over one complete cycle is 0.
- The average of 2sin(2ωt) over one complete cycle is 0.
- The average of 3sin(3ωt) over one complete cycle is 0.
- Therefore, the average value Iavg=0+0+0=0.
- The constant term is 2.
- The cosine terms are cos(ωt), 3cos(2ωt), and 3cos(3ωt).
- The average of cos(ωt) over one complete cycle is 0.
- The average of 3cos(2ωt) over one complete cycle is 0.
- The average of 3cos(3ωt) over one complete cycle is 0.
- Therefore, the average value Vavg=0+0+0+2=2.
- (i) Average value of i=4
- (ii) Average value of I=0
- (iii) Average value of V=2
Similar Questions
Knowledge Check
Out of the following functions representing motion of a particle which represents SHM?
1. x=sin3ωt
2. x=1+ωt+ω2t2
3. x=cosωt+cos3ωt+cos5ωt
4. x=sinωt+cosωtAOnly 1BOnly 1 and 3COnly 1 and 4DOnly 4
Funcation x=Asin2ωt+Bcos2ωt+Csinωtcosωt Represents SHM.
View SolutionThe average value of alternating current I=I0sinωt in time interval [0,πω] is
View SolutionWhich of the following equations can form stationary waves?
(i)y=Asin(ωt−kx) (ii) y=Acos(ωt−kx)
(iii) y=Asin(ωt+kx) (iv) y=Acos(ωt−kx) .
View SolutionWhich of the following functions of time represent (a) simple harmonic (b) periodic but not simple harmonic and (c ) non periodic motion? Give period for each case of periodic motion (ω is nay positive constant)
(1) Sin3ωt (2) 3cos(π/4−2ωt)
(3) cosωt+cos3ωt+cos5ωt
(4) e−ω2t2 (5) 1+ωt+ω2t2
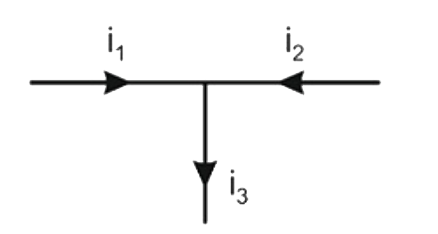
View SolutionIn the given figure, if i1=3sinωtandi2=4cosωt, then i3 is
View SolutionOut of the following functions representing motion of a particle which represents SHM?
1. x=sin3ωt
2. x=1+ωt+ω2t2
3. x=cosωt+cos3ωt+cos5ωt
4. x=sinωt+cosωt
View SolutionAn alternating current is given by
I=i1cosωt+i2sinωt.
The rms current is given by
View Solution