An emf of is applied in a circuit containing inductance and resistance. The ratio of the currents at time and is
The correct Answer is:B
To solve the problem, we need to find the ratio of the currents in an RL circuit at two different times: t=∞ and t=1s.
1. Identify the given values:
- EMF (V) = 15 V
- Inductance (L) = 5 H
- Resistance (R) = 10 Ω
2. Calculate the time constant (τ):
τ=LR=5H10Ω=0.5s
3. Determine the maximum current (I0):
The maximum current in the circuit when it reaches steady state (as t→∞) is given by:
I0=VR=15V10Ω=1.5A
4. Write the expression for current I(t) in the circuit:
The current as a function of time in an RL circuit is given by:
I(t)=I0(1−e−tτ)
5. Calculate the current at t=∞:
As t→∞:
I(∞)=I0(1−e−∞τ)=I0⋅1=1.5A
6. Calculate the current at t=1s:
Substitute t=1s into the current equation:
I(1)=1.5(1−e−10.5)=1.5(1−e−2)
Now, calculate e−2:
e−2≈0.1353(using a calculator)
Thus,
I(1)=1.5(1−0.1353)=1.5×0.8647≈1.297A
7. Find the ratio of the currents:
Now, we can find the ratio of the currents at t=∞ and t=1s:
Ratio=I(∞)I(1)=1.51.297≈1.157
Final Answer:
The ratio of the currents at t=∞ and t=1s is approximately 1.157.
- EMF (V) = 15 V
- Inductance (L) = 5 H
- Resistance (R) = 10 Ω
τ=LR=5H10Ω=0.5s
The maximum current in the circuit when it reaches steady state (as t→∞) is given by:
I0=VR=15V10Ω=1.5A
The current as a function of time in an RL circuit is given by:
I(t)=I0(1−e−tτ)
As t→∞:
I(∞)=I0(1−e−∞τ)=I0⋅1=1.5A
Substitute t=1s into the current equation:
I(1)=1.5(1−e−10.5)=1.5(1−e−2)
e−2≈0.1353(using a calculator)
Thus,
I(1)=1.5(1−0.1353)=1.5×0.8647≈1.297A
Now, we can find the ratio of the currents at t=∞ and t=1s:
Ratio=I(∞)I(1)=1.51.297≈1.157
The ratio of the currents at t=∞ and t=1s is approximately 1.157.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
An e.m.f. E=4cos(1000t)volt is applied to an LR circuit of inductance 3mH and resistance 4ohm. The amplitude of current in the circuit is
View SolutionAn alternating emf of 110 V is applied to a circuit containing a resistance R of 80Ω and an inductor L in series. The current is found to lag behind the supply voltage by an angle θ=tan1(3/4). Find the :
If the inductor has a coefficient of self inductance of 0.1 H, what is the frequency of the applied emf ?
View SolutionAn alternating emf of 110 V is applied to a circuit containing a resistance R of 80Ω and an inductor L in series. The current is found to lag behind the supply voltage by an angle θ=tan1(3/4). Find the :
Inductive reactance
View SolutionAn alternating emf of 110 V is applied to a circuit containing a resistance R of 80Ω and an inductor L in series. The current is found to lag behind the supply voltage by an angle θ=tan−1(3/4). Find the :
(i) Inductive reactance
(ii) Impedance of the circuit
(iii) Current flowing in the circuit
(iv) If the inductor has a coefficient of self inductance of 0.1 H. What is the frequency of the applied emf?
View SolutionFind the ratio of the currents at time t=∞ and t=1s, if an emf of 15V is applied in a circuit containing 5H inductance and 10Ω resistance.
View SolutionIn a LR circuit of 3 mH dinductance and 4Ω resistance, emf E=4cos1000t volt is applied. The amplitude of current is
View SolutionA 50 Hz AC signal is applied in a circuit of inductance of (1/π)H and resistance 2100Ω. The impedance offered by the circuit is
View SolutionIn the given circuit, currents through 4Ωand10Ω resistances are as shown. The current through the 5Ω resistance is _________ A.
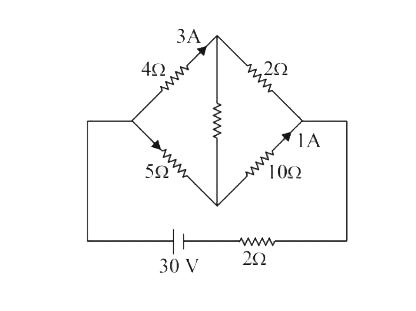
View SolutionIn the circuit shown in fig. the cell has emf 10V and internal resistance 1Ω
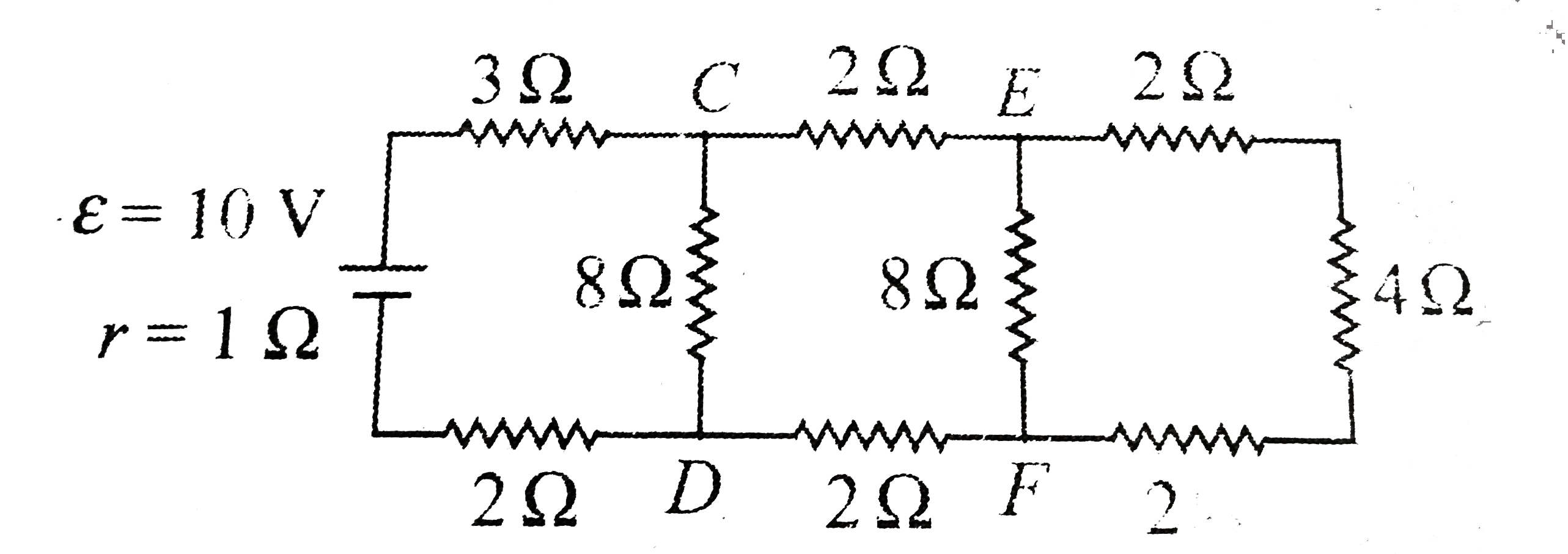
View SolutionAn alternating emf 200 volts at 50Hz is connected to a circuit resistance 1ohm and inductance 0.01H. What is the phase difference between the current and the emf in the circuit? Also, find the current in the circuit.
View Solution
