An alternating emf 200 volts at 50Hz is connected to a circuit resistance 1ohm and inductance 0.01H. What is the phase difference between the current and the emf in the circuit? Also, find the current in the circuit.
To solve the problem, we need to find the phase difference between the current and the emf in the circuit, as well as the current in the circuit. Here's a step-by-step solution:
Step 1: Calculate the Inductive Reactance (XL)
The inductive reactance XL is given by the formula:
XL=ωL
where ω=2πf and f is the frequency.
Given:
- f=50Hz
- L=0.01H
First, calculate ω:
ω=2π×50=100πrad/s
Now, calculate XL:
XL=(100π)×0.01=πΩ
Step 2: Calculate the Phase Difference (φ)
The phase difference ϕ between the current and the voltage in an R-L circuit is given by:
tan(ϕ)=XLR
Given:
- R=1Ω
Substituting the values:
tan(ϕ)=π1=π
Now, calculate ϕ:
ϕ=tan−1(π)
Using a calculator, we find:
ϕ≈72.3∘
Step 3: Calculate the Impedance (Z)
The impedance Z in an R-L circuit is given by:
Z=√R2+X2L
Substituting the values:
Z=√12+(π)2=√1+π2
Calculating Z:
Z≈√1+9.87≈√10.87≈3.30Ω
Step 4: Calculate the RMS Current (IRMS)
The RMS current IRMS can be calculated using the formula:
IRMS=VRMSZ
Given:
- VRMS=200V
Substituting the values:
IRMS=2003.30≈60.61A
Final Answers
- The phase difference ϕ≈72.3∘
- The current IRMS≈60.61A
The inductive reactance XL is given by the formula:
XL=ωL
where ω=2πf and f is the frequency.
- f=50Hz
- L=0.01H
ω=2π×50=100πrad/s
XL=(100π)×0.01=πΩ
The phase difference ϕ between the current and the voltage in an R-L circuit is given by:
tan(ϕ)=XLR
- R=1Ω
tan(ϕ)=π1=π
ϕ=tan−1(π)
ϕ≈72.3∘
The impedance Z in an R-L circuit is given by:
Z=√R2+X2L
Z=√12+(π)2=√1+π2
Z≈√1+9.87≈√10.87≈3.30Ω
The RMS current IRMS can be calculated using the formula:
IRMS=VRMSZ
- VRMS=200V
IRMS=2003.30≈60.61A
- The phase difference ϕ≈72.3∘
- The current IRMS≈60.61A
Similar Questions
An alternating emf 200 virtual volts at 50Hz is connected to a circuit resistance 1Ω and inductance 0.01H. What is the phase difference between the current and the emf in the circuit? Also, find the virtual current in the circuit.
View SolutionThe phase difference between voltage and current in series L-C circuit is
View Solution
Knowledge Check
Phase difference between voltage and current in a capacitor in an ac circuit is
AπBπ/2C0Dπ/3The phase relationship between current and voltage in a pure resistive circuit is best represented by
A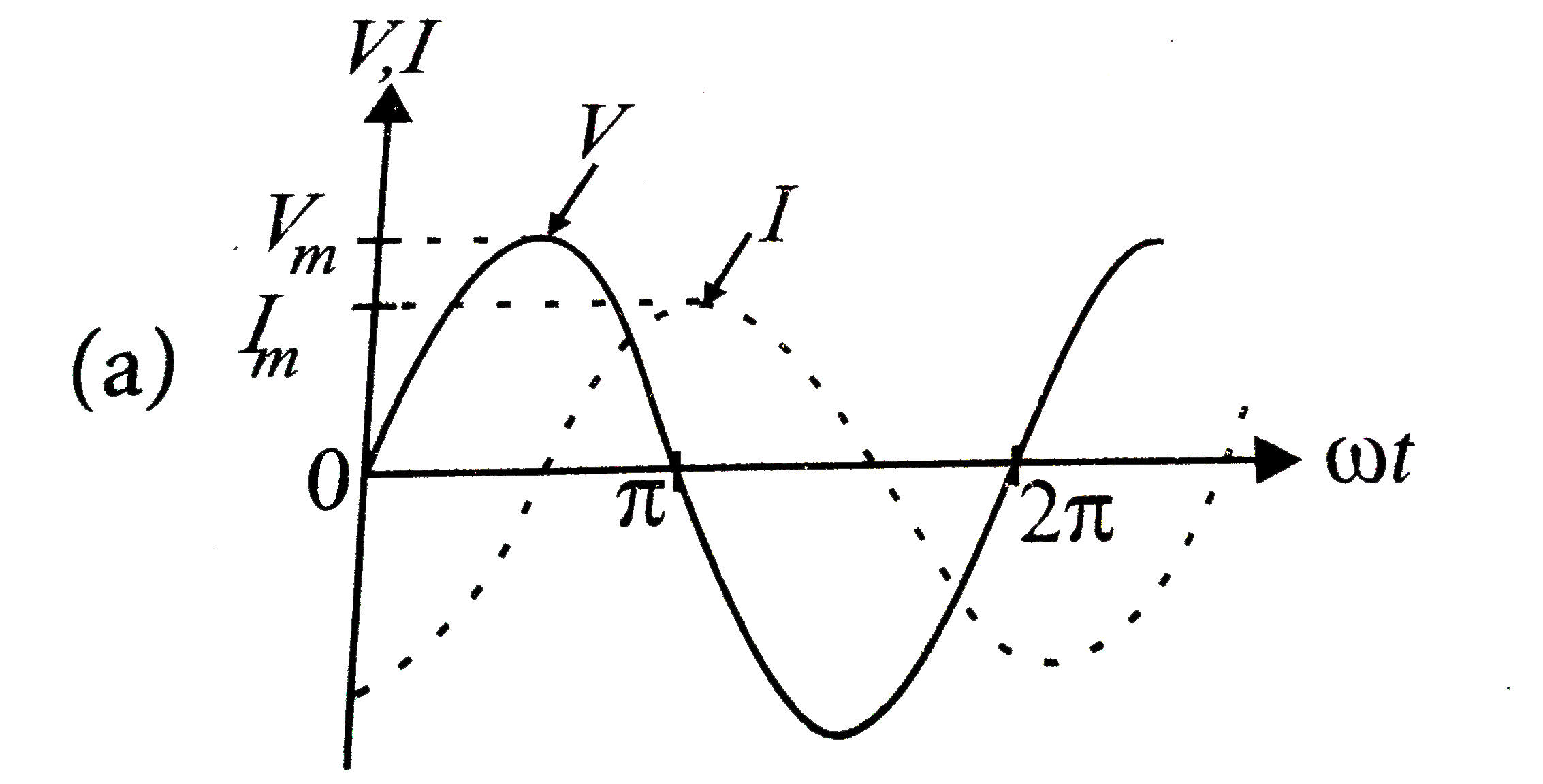 B
B C
C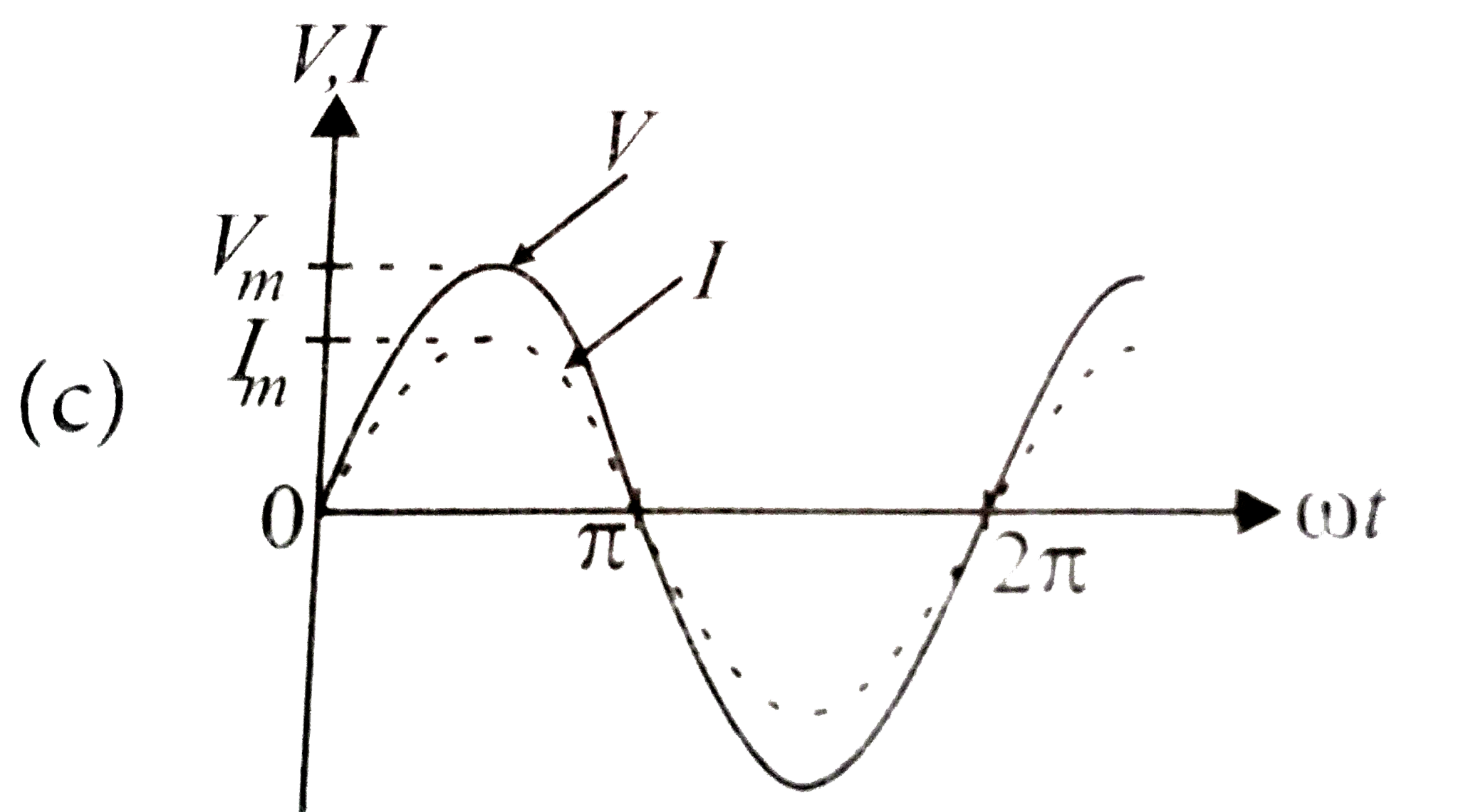 D
D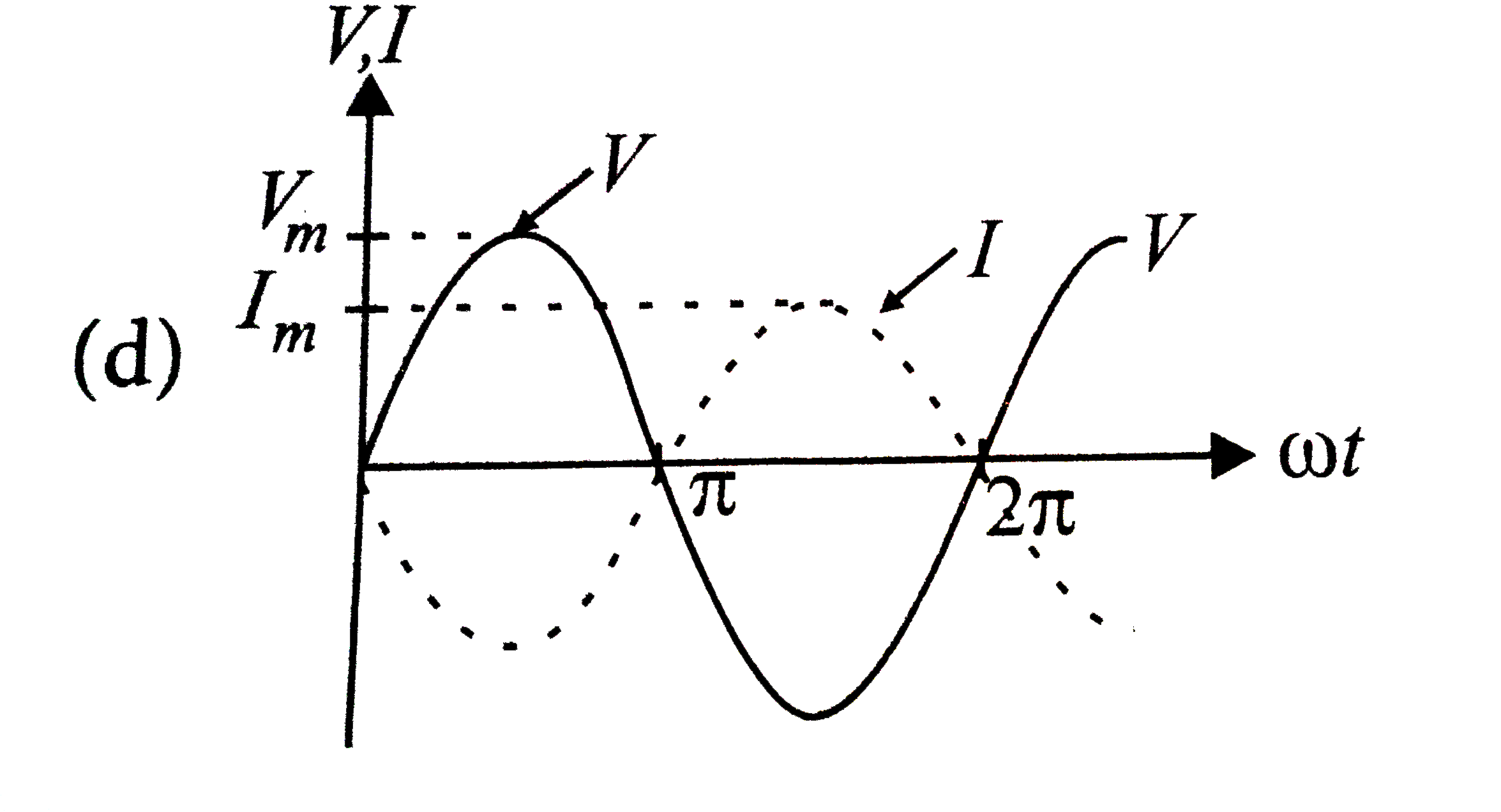
An alternating e.m.f. of 200 V and 50 cycles is connected to a circuit of resistance 3.142Ω) and inductance 0.01 H. The lag in time between the e.m.f. and the current is
View SolutionFind the phase difference between voltage and current in L-C circuit.
View SolutionThe phase angle between current and voltage in a purely inductive circuit is
View SolutionAn alternating emf of 200V, 50Hz is applied to an L-R circuit, having a resistances R of 10Ω and an inductance L of 0.05H connected in series. Calculate:
Current flowing in the circuit
View SolutionA 0.01 H inductor and √3πΩ resistance are connected in series with a 220 V, 50 Hz AC source. The phase difference between the current and emf is
View SolutionA lamp consumes only 50% of peak power in an a.c. circuit. What is the phase difference between the applied voltage and the circuit current
View Solution
