Two inductances connected in parallel are equivalent to a single inductance of 1.5H and when connected in series are equivalent to a single inductance of 8 H. The difference in their inductance is
3 H
7.5 H
2 H
4 H
The correct Answer is:D
To solve the problem of finding the difference in inductance between two inductors connected in parallel and series, we can follow these steps:
1. Define the Inductances:
Let the two inductances be L1 and L2.
2. Use the Given Information:
- When connected in parallel, the equivalent inductance is given by:
1Leq,parallel=1L1+1L2
Given Leq,parallel=1.5H, we can write:
11.5=1L1+1L2
This simplifies to:
23=1L1+1L2
- When connected in series, the equivalent inductance is:
Leq,series=L1+L2
Given Leq,series=8H, we have:
L1+L2=8
3. Set Up the Equations:
From the parallel combination, we can rearrange the equation:
1L1+1L2=23
This can be rewritten as:
L1+L2L1L2=23
Substituting L1+L2=8:
8L1L2=23
Cross-multiplying gives:
8⋅3=2⋅L1L2⟹24=2L1L2⟹L1L2=12
4. Form a Quadratic Equation:
Now we have two equations:
- L1+L2=8
- L1L2=12
We can use these to form a quadratic equation:
x2−(L1+L2)x+L1L2=0
Substituting the known values:
x2−8x+12=0
5. Solve the Quadratic Equation:
Using the quadratic formula:
x=−b±√b2−4ac2a
Here a=1,b=−8,c=12:
x=8±√(−8)2−4⋅1⋅122⋅1
x=8±√64−482
x=8±√162
x=8±42
This gives us two solutions:
x=122=6andx=42=2
Thus, L1=6H and L2=2H (or vice versa).
6. Find the Difference:
The difference in their inductances is:
|L1−L2|=|6−2|=4H
Final Answer:
The difference in their inductance is 4H.
---
Let the two inductances be L1 and L2.
- When connected in parallel, the equivalent inductance is given by:
1Leq,parallel=1L1+1L2
Given Leq,parallel=1.5H, we can write:
11.5=1L1+1L2
This simplifies to:
23=1L1+1L2
Leq,series=L1+L2
Given Leq,series=8H, we have:
L1+L2=8
From the parallel combination, we can rearrange the equation:
1L1+1L2=23
This can be rewritten as:
L1+L2L1L2=23
Substituting L1+L2=8:
8L1L2=23
Cross-multiplying gives:
8⋅3=2⋅L1L2⟹24=2L1L2⟹L1L2=12
Now we have two equations:
- L1+L2=8
- L1L2=12
x2−(L1+L2)x+L1L2=0
Substituting the known values:
x2−8x+12=0
Using the quadratic formula:
x=−b±√b2−4ac2a
Here a=1,b=−8,c=12:
x=8±√(−8)2−4⋅1⋅122⋅1
x=8±√64−482
x=8±√162
x=8±42
This gives us two solutions:
x=122=6andx=42=2
Thus, L1=6H and L2=2H (or vice versa).
The difference in their inductances is:
|L1−L2|=|6−2|=4H
The difference in their inductance is 4H.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Knowledge Check
The equivalent inductance of two inductances is 2.4 henry when connected in parallel and 10 henry when connected in series. The difference between the two inductance is
A8 H, 2HB6H, 4HC5H, 5HD7H, 3HTwo inductors of inductance L each are connected in series with opposite magnetic fluxes. The resultant inductance is
(Ignore mutual inductance)AzeroBLC2LD3L
The inductors of self inductance L1 and L2 are put in series .
View SolutionThree pure inductances each of 3H are connected as shown in figure. The equivalent inductance between points A and B is

View SolutionTwo inductors each of inductance L are connected in parallel. One more inductor of value 5 mH is connected in series of this configuration then the effective inductance is 15 mH . The value of L is ………..mH.
View SolutionAn inductance and a resistance are connected in series with an AC potential . In this circuit
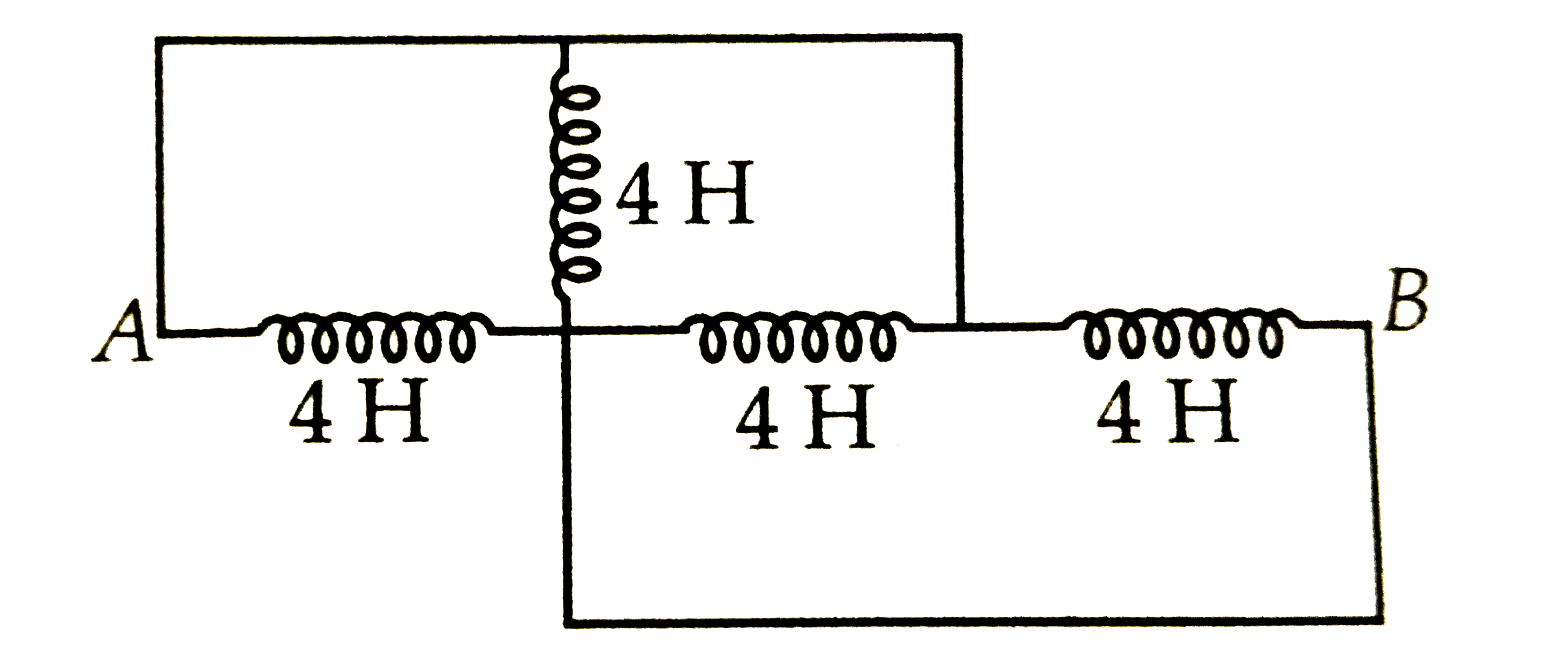
View SolutionThe equivalent inductance between A and B is
View SolutionA resistance of 40 ohms and an inductance of 95.5 millihenry are connected in series in a 50 cycle/sec AC circuit. The impedence of this combination is very nearly
View Solution