A chamber containing a gas was evacuated till the vacuum attained was 10−14 m of Hg. If the temperature of the chamber was 30∘C, the number of molecules that remains in it per cubic metre is
3.2×1011
3.2×1012
2.3×1012
2.3×1010
The correct Answer is:A
To solve the problem of finding the number of gas molecules remaining in a chamber evacuated to a vacuum of 10−14 m of Hg at a temperature of 30∘C, we can follow these steps:
Step 1: Convert the vacuum pressure from mm of Hg to Pascals
The pressure P in Pascals can be calculated using the formula:
P=density of mercury×g×h
where:
- Density of mercury (ρ) = 13600kg/m3
- Gravitational acceleration (g) = 10m/s2
- Height (h) = 10−14m
Calculating P:
P=13600kg/m3×10m/s2×10−14m=1.36×10−10Pa
Step 2: Convert the temperature from Celsius to Kelvin
To convert the temperature from Celsius to Kelvin:
T=30∘C+273.15=303.15K
Step 3: Use the ideal gas law to find the number of moles
The ideal gas law is given by:
PV=nRT
where:
- P = pressure in Pascals
- V = volume in cubic meters (1 m³)
- n = number of moles
- R = universal gas constant = 8.31J/(mol K)
- T = temperature in Kelvin
Rearranging for n:
n=PVRT
Substituting the values:
n=(1.36×10−10Pa)(1m3)(8.31J/(mol K))(303.15K)
Calculating n:
n=1.36×10−108.31×303.15≈5.4×10−12mol
Step 4: Calculate the number of molecules
The number of molecules N can be calculated using Avogadro's number (NA=6.02×1023molecules/mol):
N=n×NA
Substituting the values:
N=(5.4×10−12mol)×(6.02×1023molecules/mol)≈3.25×1012molecules
Final Answer
The number of molecules that remain in the chamber per cubic meter is approximately 3.2×1012.
The pressure P in Pascals can be calculated using the formula:
P=density of mercury×g×h
where:
- Density of mercury (ρ) = 13600kg/m3
- Gravitational acceleration (g) = 10m/s2
- Height (h) = 10−14m
P=13600kg/m3×10m/s2×10−14m=1.36×10−10Pa
To convert the temperature from Celsius to Kelvin:
T=30∘C+273.15=303.15K
The ideal gas law is given by:
PV=nRT
where:
- P = pressure in Pascals
- V = volume in cubic meters (1 m³)
- n = number of moles
- R = universal gas constant = 8.31J/(mol K)
- T = temperature in Kelvin
n=PVRT
Substituting the values:
n=(1.36×10−10Pa)(1m3)(8.31J/(mol K))(303.15K)
n=1.36×10−108.31×303.15≈5.4×10−12mol
The number of molecules N can be calculated using Avogadro's number (NA=6.02×1023molecules/mol):
N=n×NA
Substituting the values:
N=(5.4×10−12mol)×(6.02×1023molecules/mol)≈3.25×1012molecules
The number of molecules that remain in the chamber per cubic meter is approximately 3.2×1012.
Topper's Solved these Questions
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - B medical entrance special format questions
14 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Match the columns
5 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Check point 14.4
25 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Subjective
9 Videos
Similar Questions
In a very good vacuum system in the laboratory, the vacuum attained was 10−13atm. If the temperature of the system was 300K, the number of molecules present in a volume of 1cm3 is.
View SolutionA discharge tube of 2 litre capacity containing hydrogen gas was evacuated till the pressure inside is 1×10−5 atm. If the tube is maintained at a temperature of 27∘C, calculate the number of hydrogen molecules still present in the tube.
View SolutionThe pressure inside an electric bulb is 10−3mm of Hg at a temperature of 25∘C. If the volume of the bulb is 10−4m3, find the number of molecules contained in it.
View SolutionA container of negligible heat capacity contains 1kg of water. It is connected by a steel rod of length 10m and area of cross-section 10cm2 to a large steam chamber which is maintained at 100∘C. If initial temperature of water is 0∘C, find the time after which it beomes 50∘C. (Neglect heat capacity of steel rod and assume no loss of heat to surroundings) (use table 3.1, take specific heat of water =4180J/kg.∘C)
View SolutionAir entering the lungs ends up in tiny sacs called alveoli.From the alveoli, the oxygen diffuses into the blood. The average radius of the alveoli is 0.0050 cm and the air inside contains 14 per cent oxygen. Assuming that the pressure in the alveoli is 1.0 atm and the temperature is 37∘C, calculate the number of oxygen molecules in one of the alveoli.
View SolutionThe figure given below shows three glass chambers that are connected by valves of negligible volume. At the outset of an experiment, the valves are closed and the chambers contain the gases as detailed in the diagram. All the chambers are at the temperature of 300K and external pressure of 1.0atm.
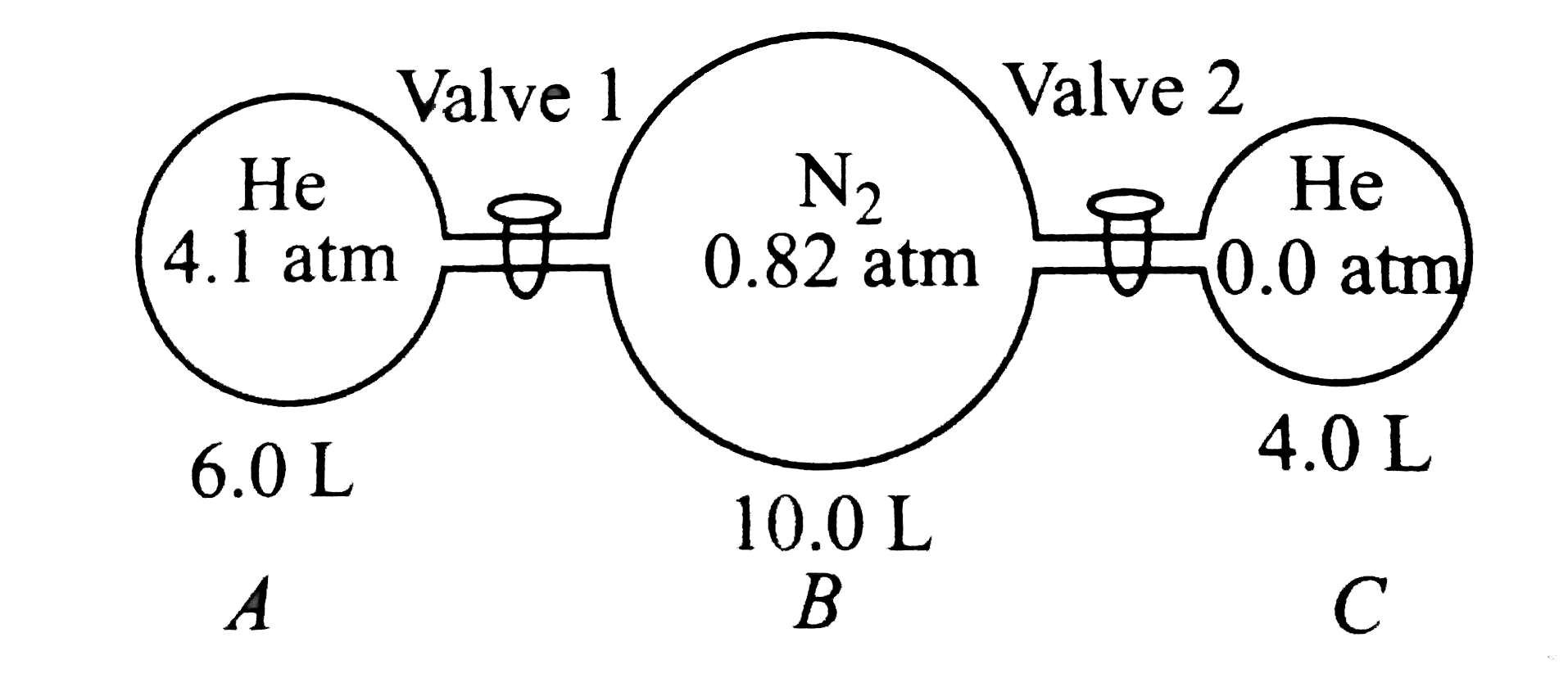
Which of the following represents the total kinetic energy of all the gas molecules after both valves are opened?
(R=0.082atmLK−1mol−1=8.314JK_1mol−1)
View SolutionA gas is to be filled from a tank of capacity 10,000 litres into cylinders each having capacity of 10 litres. The condition of the gas in the tank is as follows:
Pressure inside the tank is 800 mm Hg.
Temperature inside the tank is −3∘C.
When the cylinder is filled, the pressure gauge reads 400 mm of Hg and the temperature is 270 K. Find the number of cylinders required to fill the gas.
View Solution10dm3 of N2 gas and 10dm3 of gas X contain the same number of molecules at the same temperature, the gas (X) may be
View SolutionA flask containing 12g of a gas relative molecular mass 120at a pressure of 100atm was evacuated by means of a pump until the pressure was 0.01atm. Which of the following in the best estimate of the number of molecules left in the flask (N0=6×1023mol−1)?
View SolutionA sphere of aluminium of 0.047 kg is placed for sufficient time in a vessel containing boiling water, so that the sphere is at 100∘ C. It is then immediately transferred to 0.14 kg copper calorimeter containing 0.25 kg of water at 20∘ C. The temperature of water rises and attains a steady state at 23∘Calculate the specific heat capacity of aluminium. (Give specific heat of copper =0.386×103Jkg−1K−1).
View Solution
