An ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
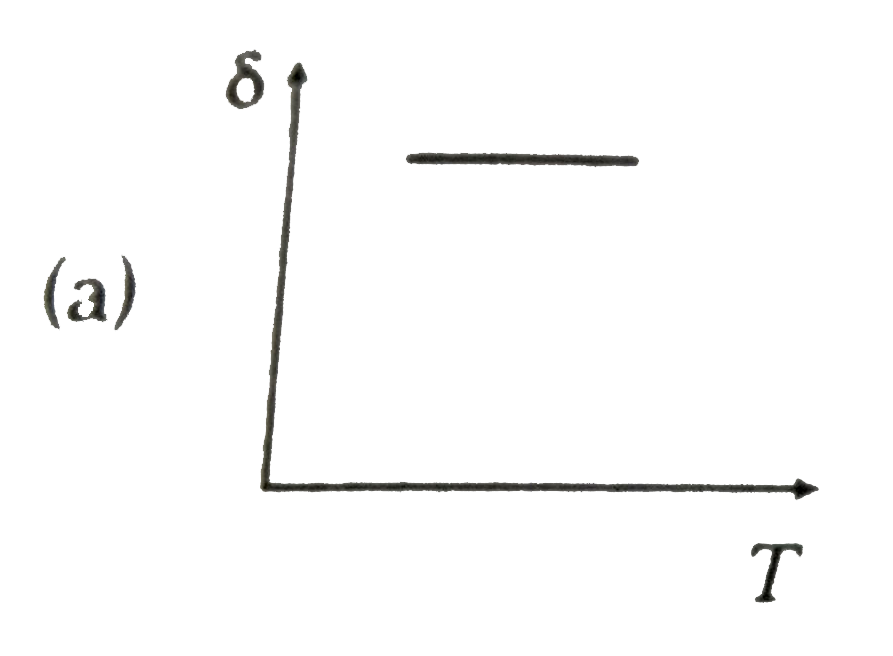
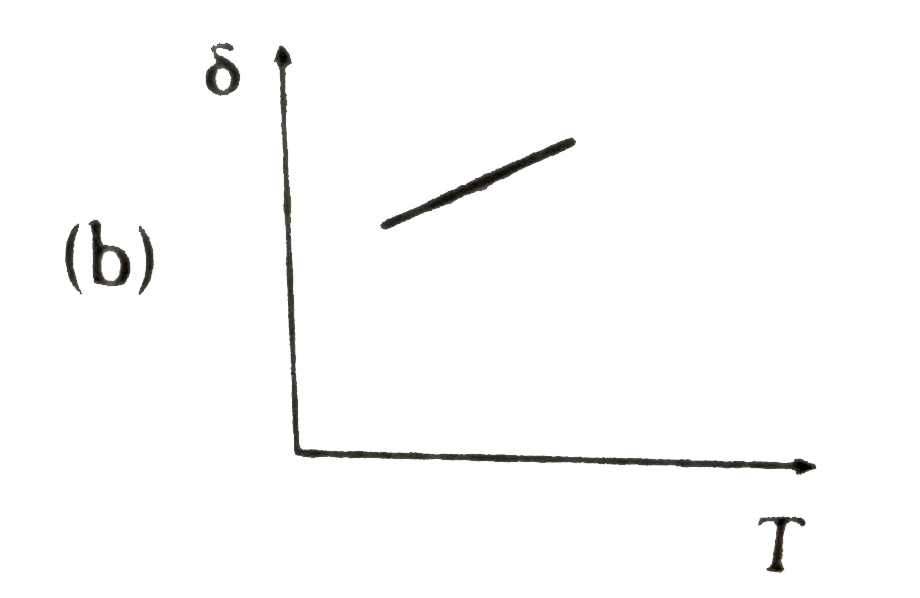

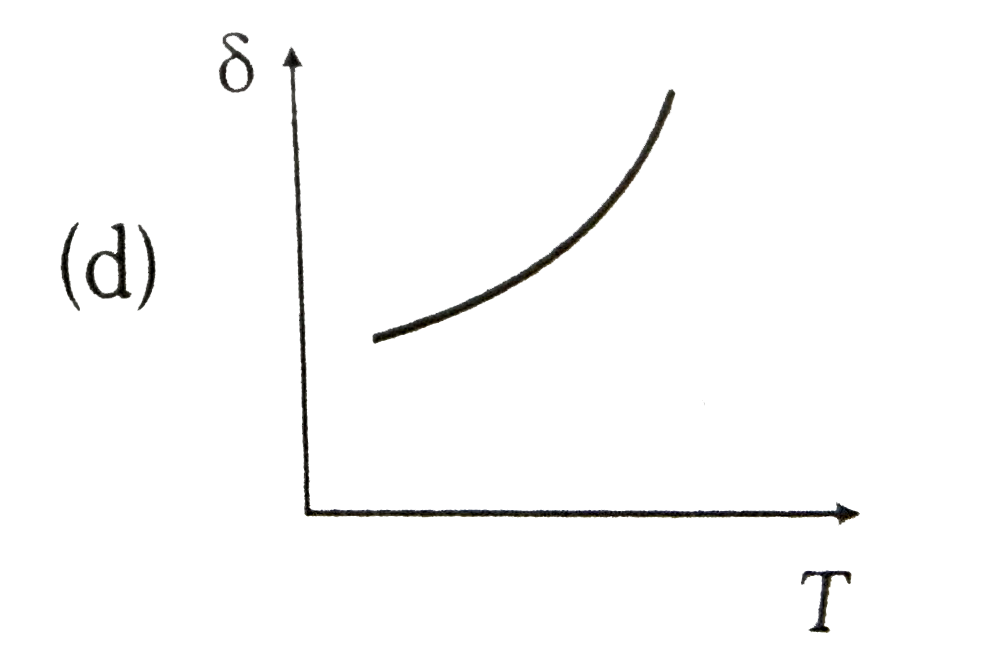
The correct Answer is:C
To solve the problem step by step, we will use the ideal gas law and the relationship between volume, temperature, and pressure.
Step 1: Understand the Ideal Gas Law
The ideal gas law is given by the equation:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles of gas
- R = universal gas constant
- T = temperature
Step 2: Analyze the Situation
We are given that:
- The initial volume of the gas is V.
- The volume increases by ΔV due to an increase in temperature ΔT.
- The pressure remains constant.
Step 3: Apply the Ideal Gas Law
Since the pressure is constant, we can express the change in volume as:
PΔV=nRΔT
Step 4: Rearranging the Equation
Dividing both sides by PV gives:
ΔVV=nRΔTPV
Step 5: Substitute for Pressure
From the ideal gas law, we can express pressure as:
P=nRTV
Substituting this into the equation gives:
ΔVV=nRΔT(nRTV)V
Step 6: Simplifying the Equation
This simplifies to:
ΔVV=ΔTT
Thus, we can express the change in volume per unit volume and temperature as:
ΔVVΔT=1T
Step 7: Define the Quantity δ
Let:
δ=ΔVVΔT
From our previous step, we have:
δ=1T
Step 8: Analyze the Variation of δ with Temperature
As T increases, δ decreases, indicating an inverse relationship. Therefore, δ varies with temperature as:
δ∝1T
Step 9: Graphical Representation
The relationship δT=constant indicates that if we plot δ against T, we will get a rectangular hyperbola.
Conclusion
Thus, the quantity δ=ΔVVΔT varies with temperature T as δ∝1T, and the correct option is that the graph of δ versus T is a rectangular hyperbola.
The ideal gas law is given by the equation:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles of gas
- R = universal gas constant
- T = temperature
We are given that:
- The initial volume of the gas is V.
- The volume increases by ΔV due to an increase in temperature ΔT.
- The pressure remains constant.
Since the pressure is constant, we can express the change in volume as:
PΔV=nRΔT
Dividing both sides by PV gives:
ΔVV=nRΔTPV
From the ideal gas law, we can express pressure as:
P=nRTV
Substituting this into the equation gives:
ΔVV=nRΔT(nRTV)V
This simplifies to:
ΔVV=ΔTT
Thus, we can express the change in volume per unit volume and temperature as:
ΔVVΔT=1T
Let:
δ=ΔVVΔT
From our previous step, we have:
δ=1T
As T increases, δ decreases, indicating an inverse relationship. Therefore, δ varies with temperature as:
δ∝1T
The relationship δT=constant indicates that if we plot δ against T, we will get a rectangular hyperbola.
Thus, the quantity δ=ΔVVΔT varies with temperature T as δ∝1T, and the correct option is that the graph of δ versus T is a rectangular hyperbola.
Topper's Solved these Questions
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - B medical entrance special format questions
14 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Match the columns
5 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Check point 14.4
25 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Subjective
9 Videos
Similar Questions
Knowledge Check
As the temperature increases, average kinetic energy of molecules increases. What would be the effect of increase of temperature on pressure provided the volume is constant ?
AIncreasesBDecreasesCRemains sameDBecomes half
Can the temperature of a gas increased keeping its pressure and volume constant ?
View SolutionTemperature of an ideal gas increases in:
View SolutionBy increasing temperature of a gas by 6∘C its pressure increases by 0.4%, at constant volume. Then initial temperature of gas is
View SolutionAt constant temperature if the pressure of an ideal gas is increased by 10% then its volume must decrease by
View SolutionAt constant temperature if the pressure of an ideal gas is increased by 10% then its volume must decrease by
View SolutionAs the temperature increases, average kinetic energy of molecules increases. What would be the effect of increase of temperature on pressure provided the volume is constant ?
View SolutionWhen volume of system is increased two times and temperature is decreased half of its initial temperature, then pressure becomes ………….
View Solution