A mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars (figure). A mass m is suspended from the mid-point of the wire. Strain in the wire is
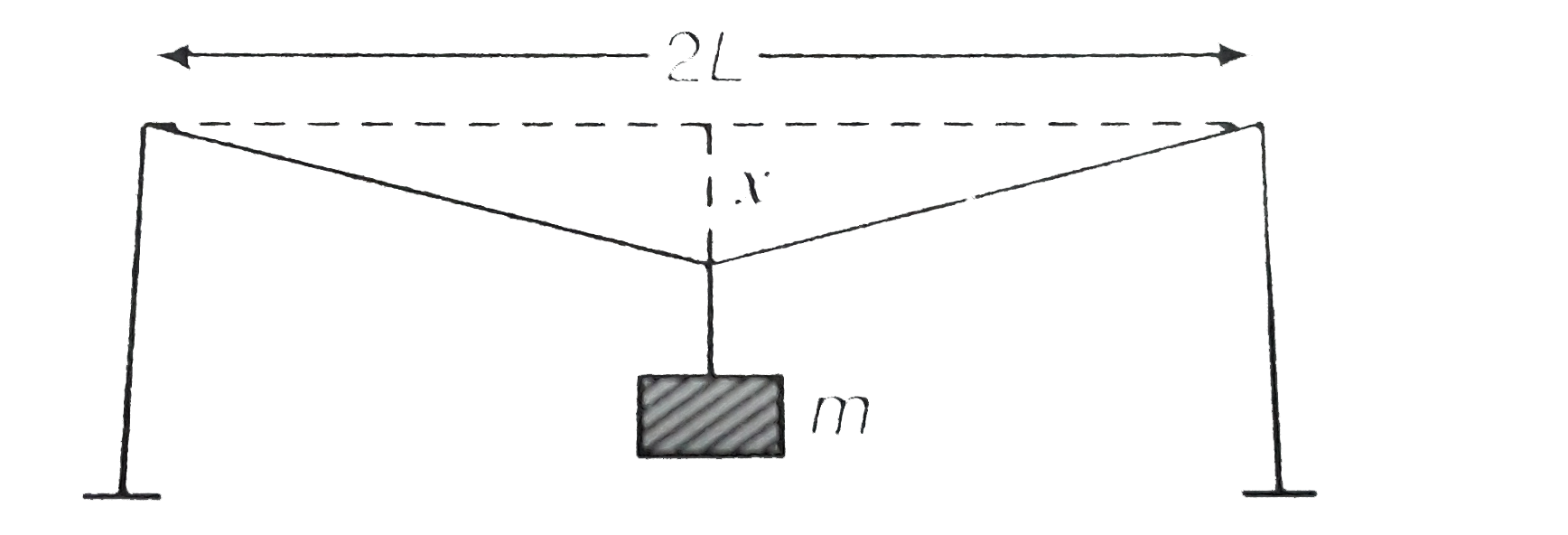
x22L2
xL
x2/L
x2/2L
The correct Answer is:A
(a) Consider the diagram below
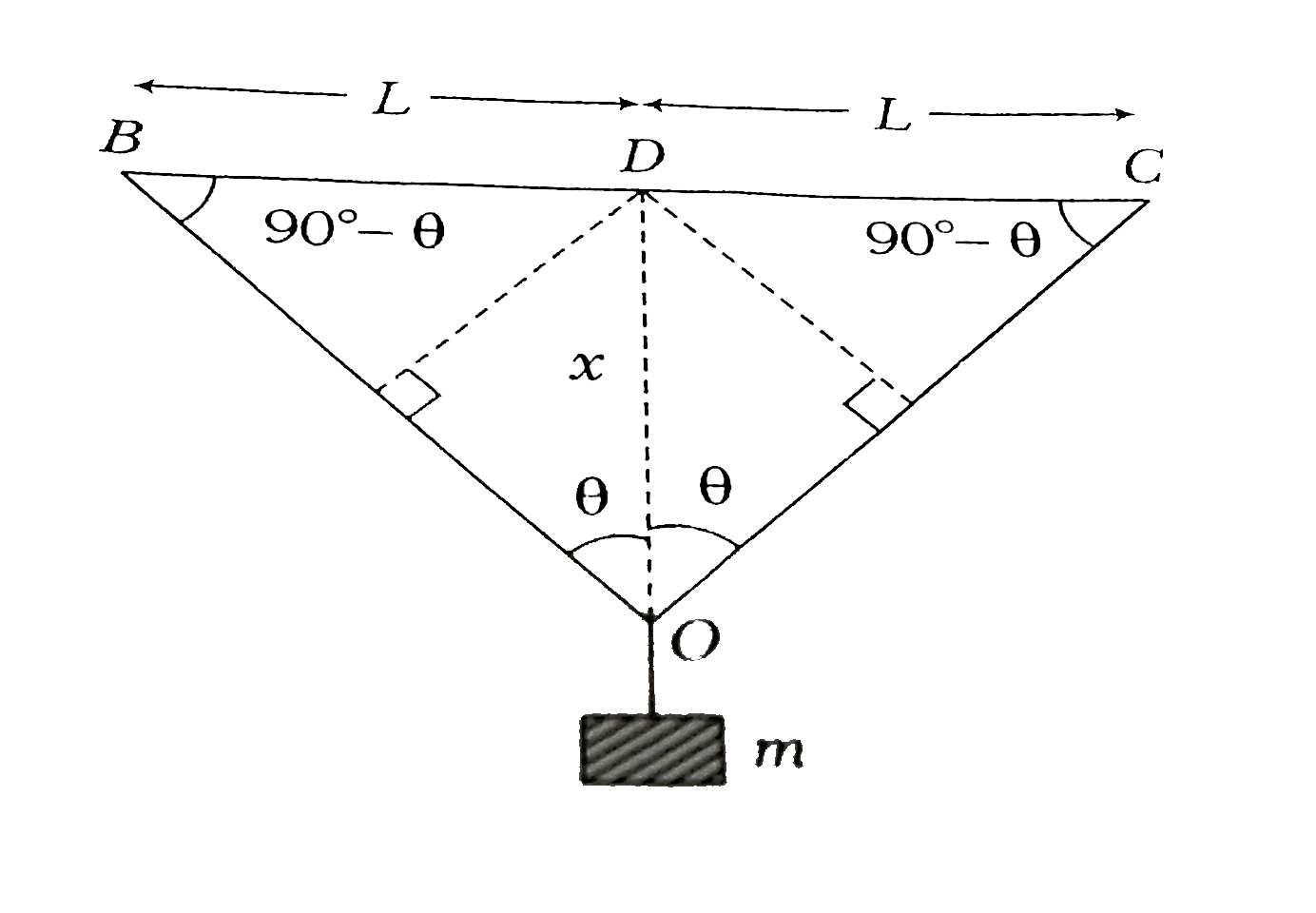
Hence, change in length
ΔL=BO+OC−(BD+DC)
=2BO−2BD(∵BO=OC,BD=DC)
=2[BO−BD]=2[(x2+L2)1/2−L]
=2L[(1+x2L2)1/2−1]≈2L[1+12x2L2−1]=x2L[∵x<<L]
∴ Strain =ΔL2L=x2/L2L=x22L2
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Match the columns
4 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.3
15 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
469 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
A mild steel wire of length 1.0m and cross sectional area 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
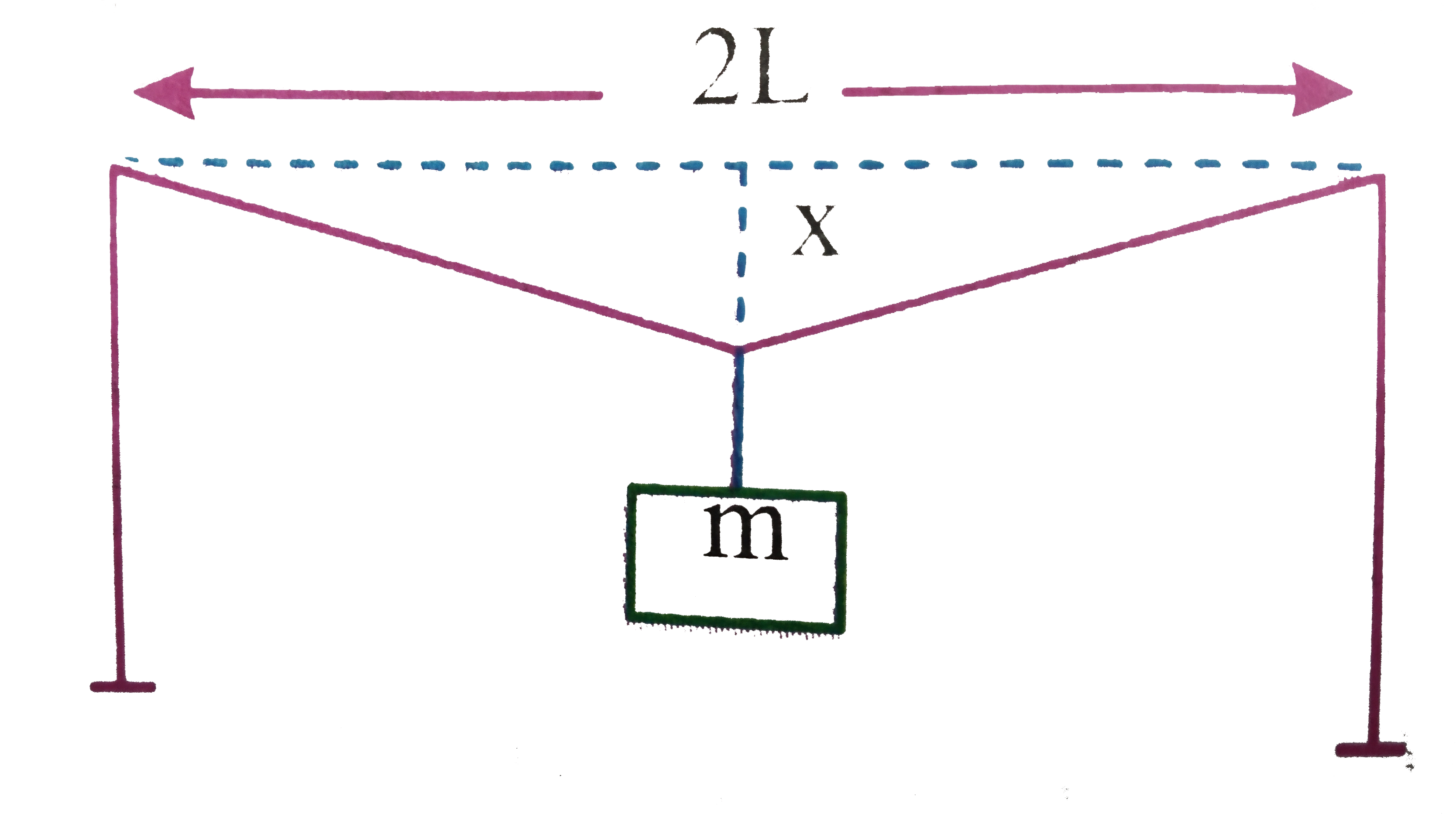
View SolutionA steel wire of length 2L and cross-section area A is stretched, wetl within elastic limit horizontally between two pillars, a mass m is suspended from the mid-point of wire such that depression at the middle is x. Strain in the wire is proportional to
View Solution
Knowledge Check
A mild steel wire of length 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
 Ax22L2BxLCx2LDx22L
Ax22L2BxLCx2LDx22LA metal wire of length L1 and area of cross section A is attached to a rigid support. Another metal wire of length L2 and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if Y1 and Y2 are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
A[(Y1Y2)A][2(Y1L2+Y2L1)]B[(Y1Y2)A](L1L2)2C[(Y1Y2)A](Y1L2+Y2L1)D[(Y1Y2)1/2A](L2+L1)1/2A metal wire of length L1 and area of cross section A is ttached to a rigid support. Another metal wire of length L2 and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if Y1 and Y2 are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
AY1Y2A2(Y1L2+Y2L1)BY1Y2A(L1L2)1/2CY1Y2A(Y1L2+Y2L1)D(Y1Y2)1/2A(L1L2)1/2
A mild steel wire of length 1.0 m and cross-sectional are 0.5×10−2cm2 is streached, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid point of the wire, calculate the depression at the mid point.
g=10ms−2,Y=20×1011Nm−2.
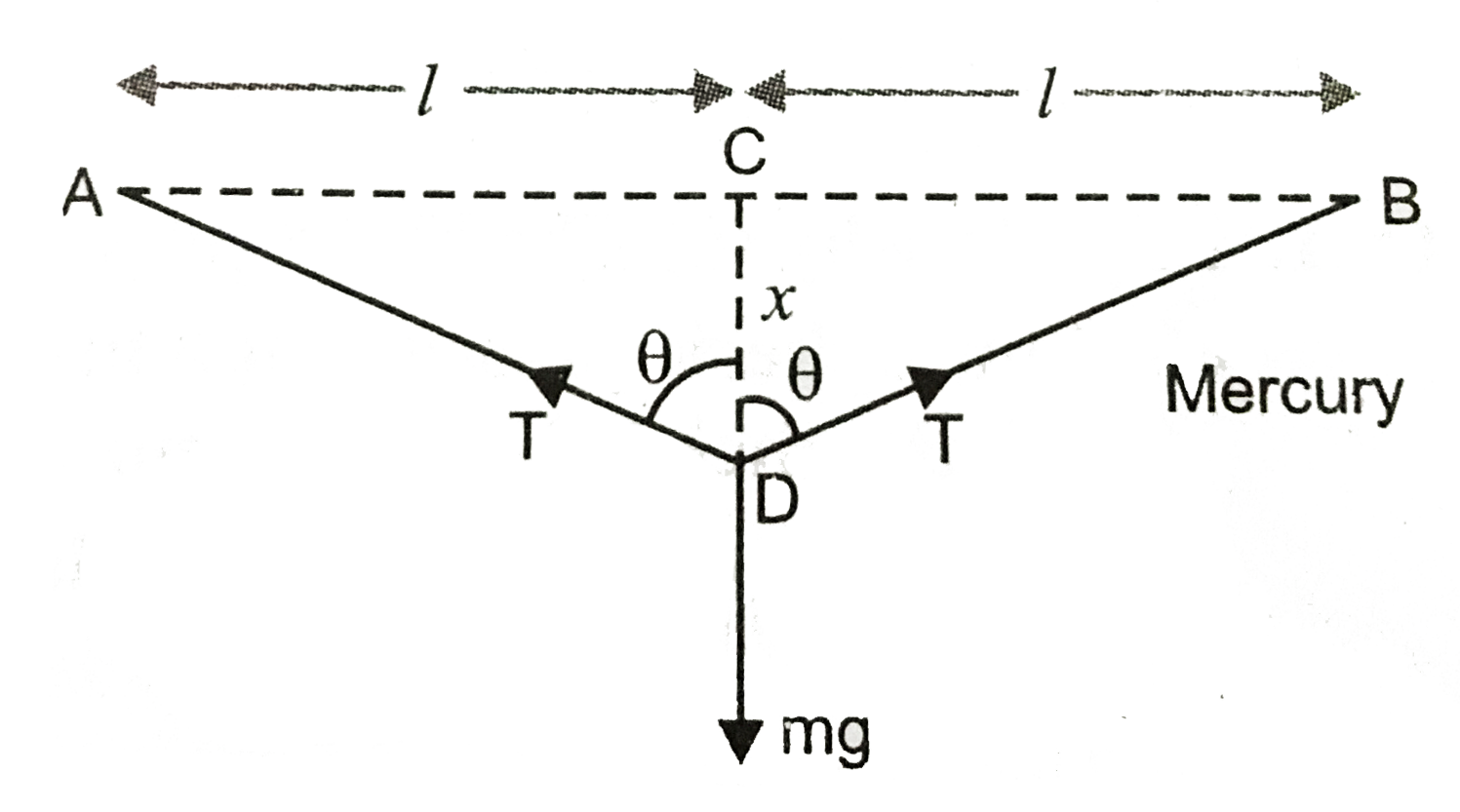
View SolutionA wire of cross section A is stretched horizontally between two clamps located 2lm apart. A weight Wkg is suspended from the mid-point of the wire. If the mid-point sags vertically through a distance x<l, the strain produced is
View SolutionA steel wire of negligible mass, length 2I, cross sectional area 'A' and Young's modulus 'Y' is held between two rigid walls. A small body of mass 'm' is suspended from its middle point 'O' as shown. The vertical descent of the middle point 'O' of the wire is

View SolutionA wire of uniform cross-sectional area A and young's modulus Y is stretched within the elastic limits. If s is stress in the wire, the elastic energy density stored in the wire in terms of the given parameters is
View SolutionA wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
View Solution
