A spring has a natural length of 50 cm and a force constant of 2.0×103 Nm−1. A body of mass 10 kg is suspended from it and the spring is stretched. If the body is pulled down to a length of 58 cm and released, it executes simple harmonic motion. The net force on the body when it is at its lowermost position of its oscillation is (10x) newton. Find value of x. (Take g=10m/s2)
20 N
40 N
60 N
80 N
The correct Answer is:C
To solve the problem step by step, we will analyze the forces acting on the mass when it is in simple harmonic motion.
Step 1: Identify the given data
- Natural length of the spring, L0=50cm=0.5m
- Force constant of the spring, k=2.0×103N/m
- Mass of the body, m=10kg
- Gravitational acceleration, g=10m/s2
- Stretched length of the spring when pulled down, L=58cm=0.58m
Step 2: Calculate the equilibrium position
At equilibrium, the force exerted by the spring equals the weight of the mass:
mg=kx0
Where x0 is the elongation from the natural length at equilibrium.
Calculating mg:
mg=10kg×10m/s2=100N
Now, substituting into the equilibrium equation:
100=2000×x0
Solving for x0:
x0=1002000=0.05m=5cm
Step 3: Determine the total elongation when pulled down
When the body is pulled down to a length of 58 cm, the total elongation x from the natural length is:
x=L−L0=0.58m−0.5m=0.08m=8cm
Step 4: Calculate the net force at the lowermost position
At the lowermost position, the net force Fnet acting on the mass is given by the difference between the weight of the mass and the spring force:
Fnet=mg−kx
Substituting the values:
Fnet=100N−(2000N/m×0.08m)
Calculating the spring force:
kx=2000×0.08=160N
Now substituting back:
Fnet=100N−160N=−60N
Step 5: Relate the net force to the value of x
The problem states that the net force is 10x Newtons. Thus:
−60=10x
Solving for x:
x=−6N
Since we are interested in the magnitude:
|x|=6
Final Answer
The value of x is 6.
---
- Natural length of the spring, L0=50cm=0.5m
- Force constant of the spring, k=2.0×103N/m
- Mass of the body, m=10kg
- Gravitational acceleration, g=10m/s2
- Stretched length of the spring when pulled down, L=58cm=0.58m
At equilibrium, the force exerted by the spring equals the weight of the mass:
mg=kx0
Where x0 is the elongation from the natural length at equilibrium.
mg=10kg×10m/s2=100N
100=2000×x0
Solving for x0:
x0=1002000=0.05m=5cm
When the body is pulled down to a length of 58 cm, the total elongation x from the natural length is:
x=L−L0=0.58m−0.5m=0.08m=8cm
At the lowermost position, the net force Fnet acting on the mass is given by the difference between the weight of the mass and the spring force:
Fnet=mg−kx
Fnet=100N−(2000N/m×0.08m)
Calculating the spring force:
kx=2000×0.08=160N
Fnet=100N−160N=−60N
The problem states that the net force is 10x Newtons. Thus:
−60=10x
Solving for x:
x=−6N
Since we are interested in the magnitude:
|x|=6
The value of x is 6.
Similar Questions
A spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
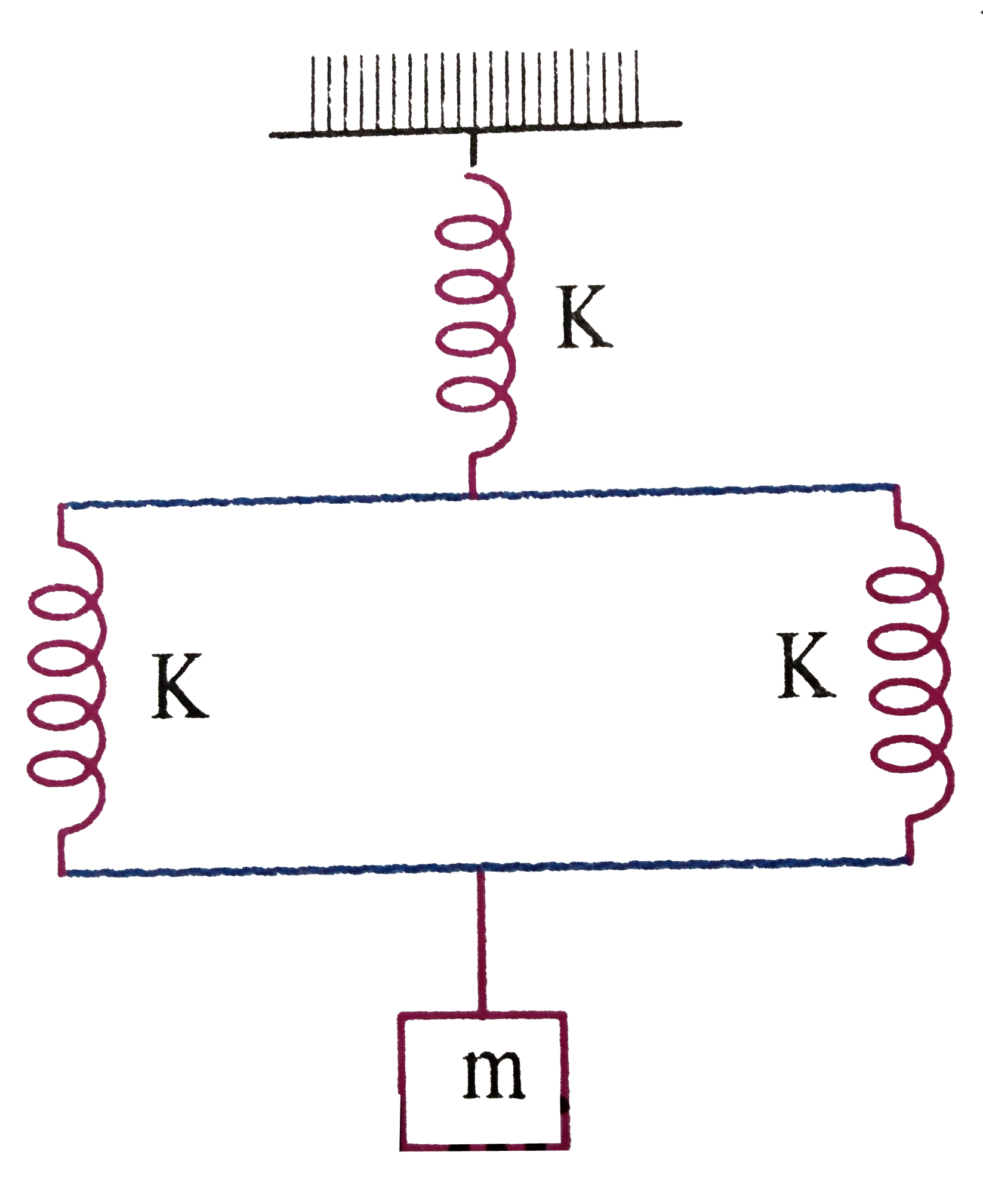
View Solution
Knowledge Check
A mass of 1 kg suspended from a spring whose force constant is 400 Nm−1, executes simple harmonic motion. When the energy of the oscillator is 2J, the maximum acceleration experienced by maas will be
A2ms−2B4ms−2C40ms−2D400ms−2Natural length of a spring is 60 cm and its spring constant is 4000 N/m. A mass of 20 kg is hung from it. The extension produced in the spring is (Take, g=9.8m/s2)
A4.9 cmB0.49 cmC9.4 cmD0.94 cm
The force constant of a weightless spring is 16Nm−1. A body of mass 1.0kg suspended from it is pulled down through 5cm and then released. The maximum energy of the system (spring + body) will be
View SolutionForce constant of a weightless spring is 16Nm−1. A body if mass 1 kg suspended from it is pulled down through 5 cm from its mean position and then released. The maximum kinetic energy of the body will be
View SolutionA paricle of mass 30kg executes a simple harmonic motion. The restorting force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA particle of mass 200g executes a simple harmonic motion. The restoring force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA body of mass 10 kg is suspended by a string and is pulled a side with a horizontal force of 49 N. Find the tension in the string, if the body is in equilibrium under these forces.
View Solution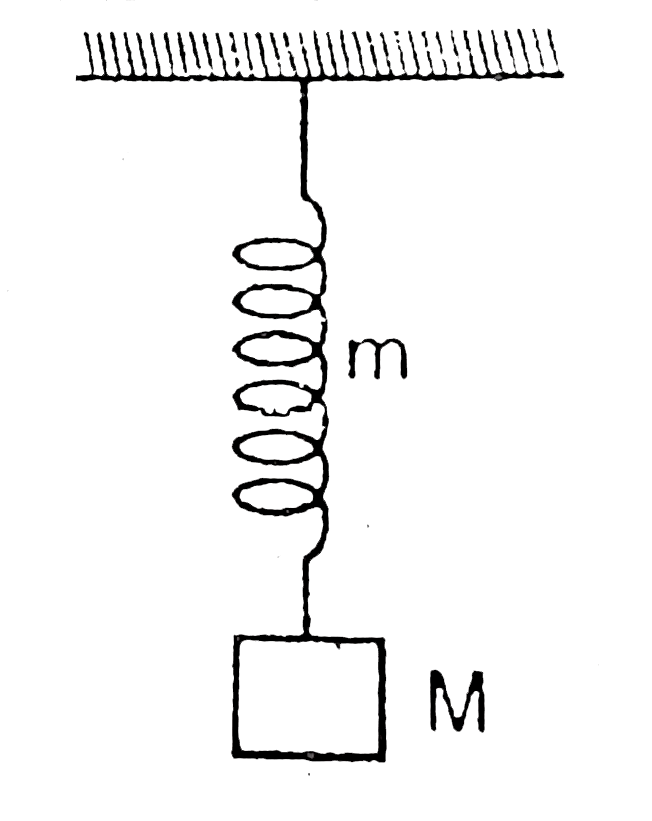
A block of M is suspended from a vertical spring of mass m as shown in the figure. When block is pulled down and released the mass oscillates with maximum velocity v.
View Solution
