A particle is moving with constant angular velocity along the circumference of a circle. Which of the following statements is true
The particle executes SHM
Non-periodic motion
The projection of the particle on any of the diameters executes SHM
None of the above
The correct Answer is:C
To solve the question regarding the motion of a particle moving with constant angular velocity along the circumference of a circle, we will analyze each of the given options step by step.
Step 1: Understand the Motion
The particle is moving along the circumference of a circle with a constant angular velocity (ω). This means that the particle completes equal angles in equal intervals of time, which is characteristic of periodic motion.
Hint: Remember that constant angular velocity implies that the particle will return to the same position after a certain time period.
Step 2: Analyze Option 1
Option 1 states that the particle executes simple harmonic motion (SHM). For a motion to be classified as SHM, it must be periodic and exhibit a to-and-fro motion about an equilibrium position. In this case, while the motion is periodic, it does not exhibit to-and-fro motion; it moves continuously around the circle.
Hint: SHM requires oscillation about an equilibrium position, which is not the case here.
Step 3: Analyze Option 2
Option 2 claims that the motion is non-periodic. Since the particle moves with constant angular velocity, it returns to its starting position after a fixed time period, indicating that the motion is periodic.
Hint: Periodic motion is characterized by the repetition of the same motion after a fixed time interval.
Step 4: Analyze Option 3
Option 3 states that the projection of the particle on any diameter executes simple harmonic motion. If we project the motion of the particle onto a diameter of the circle, the projection will move back and forth between two extremes as the particle moves around the circle. This projection indeed exhibits to-and-fro motion about the center, making it simple harmonic motion.
Hint: Consider how the projection behaves as the particle moves; it should oscillate back and forth.
Step 5: Analyze Option 4
Option 4 states that none of the above options are correct. However, we have established that option 3 is indeed correct.
Hint: Always check if any of the previous options are valid before concluding that none are correct.
Conclusion
After analyzing all the options, we conclude that the correct statement is:
The projection of the particle on any of the diameter executes simple harmonic motion.
Final Answer
Option 3 is true.
The particle is moving along the circumference of a circle with a constant angular velocity (ω). This means that the particle completes equal angles in equal intervals of time, which is characteristic of periodic motion.
Option 1 states that the particle executes simple harmonic motion (SHM). For a motion to be classified as SHM, it must be periodic and exhibit a to-and-fro motion about an equilibrium position. In this case, while the motion is periodic, it does not exhibit to-and-fro motion; it moves continuously around the circle.
Option 2 claims that the motion is non-periodic. Since the particle moves with constant angular velocity, it returns to its starting position after a fixed time period, indicating that the motion is periodic.
Option 3 states that the projection of the particle on any diameter executes simple harmonic motion. If we project the motion of the particle onto a diameter of the circle, the projection will move back and forth between two extremes as the particle moves around the circle. This projection indeed exhibits to-and-fro motion about the center, making it simple harmonic motion.
Option 4 states that none of the above options are correct. However, we have established that option 3 is indeed correct.
After analyzing all the options, we conclude that the correct statement is:
Option 3 is true.
Similar Questions
A particle moves with constant angular velocity in a circle. During the motion its
View SolutionA particle is moving with constant speed V m/s along the circumference of a circle of radius R meters as shown. A, B and C are three points on periphery of the circle and ΔABC is equilateral. The magnitude of average velocity of particle, as it moves from A to C in clockwise sence, will be :
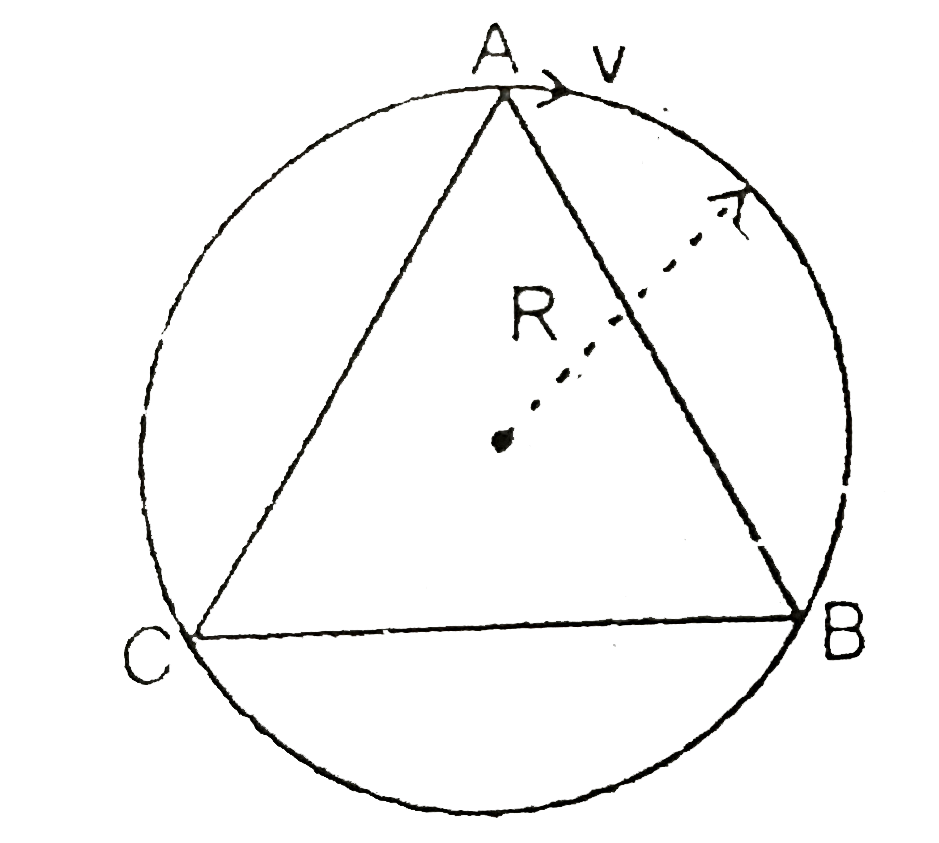
View Solution
Knowledge Check
A charged particle would continue to move with a constant velocity in a region wherein, which of the following conditions is not correct?
AE=0,B≠0BE≠0,B≠0CE≠0,B=0DE=0,B=0A particle moves along the circumference of a circle of radius r when its completes one rotation.
ADistance travelled is zero and displacement is 2πrBdistance and displacement are zeroCdistance is 2πr but displacement is zeroDdistance and displacement are 2πr each
The diagram shows a train moving with constant velocity and a car moving towards the train with constant velocity. The engine driver measures the velocity of the car as v1 . The passenger sitting in the last compartment measures the velocity of the car as v2 . Which of the following statements is true?

View SolutionA particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
View SolutionTwo particles AandB move on a circle Initially, particles AandB are diagonally opposite to each other. Particle A moves with angular velocity πrads−1 and angular acceleration π/2rads−2 and particle B moves with constant angular velocity 2πrads−2. Find the time after which both the particlsd AnadB will collide.
View SolutionA particle is moving along a circular path. The angular velocity, linear velocity, Angular acceleration, and centripetal acceleration of the particle at any instant. Respectively are →ω,→v,→∝,and→ac. Which of the following relations is not correct ?
View SolutionThe potential energy of a particle of mass ? at a distance ? from a fixed point ? is given by V(r)=kr2/2, where ? is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius ? about the point ?. If ? is the speed of the particle and ? is the magnitude of its angular momentum about ?, which of the following statements is (are) true?
View SolutionWhat is the torque acting on a body moving with constant angular velocity ?
View Solution

