A hockey player is moving northward and suddenly turns westward with the same speed to avoid an opponet. The force that acts on the player is.
frictional force along westward
muscle force along southward
frictional force along south-west
muscle force along south-west
The correct Answer is:C
To solve the problem of the hockey player turning from moving northward to westward, we need to analyze the situation in terms of momentum and the change in direction. Here’s a step-by-step solution:
Step 1: Understand the Initial and Final Directions
The hockey player is initially moving northward. We can represent this direction as a vector pointing upwards on a graph. When the player turns westward, the direction changes to the left on the graph.
Hint: Visualize the directions on a coordinate system where north is up and west is left.
Step 2: Represent the Initial and Final Momentum
Let’s denote the initial momentum of the player moving northward as P1 and the final momentum when the player turns westward as P2. Since the speed remains the same, the magnitudes of these momentum vectors will be equal, but their directions will differ.
Hint: Remember that momentum is a vector quantity, which means it has both magnitude and direction.
Step 3: Draw the Vectors
Draw a diagram where:
- The vector P1 points north (upward).
- The vector P2 points west (to the left).
This creates a right-angled triangle where the change in momentum can be visualized.
Hint: Use arrows to represent the direction and length of the momentum vectors accurately.
Step 4: Calculate the Change in Momentum
The change in momentum ΔP can be calculated as:
ΔP=P2−P1
Since the player is changing direction, the resultant vector will be diagonal, pointing southwest.
Hint: The change in momentum is not just a simple subtraction; consider the vector nature of momentum.
Step 5: Determine the Direction of the Resultant Force
The resultant change in momentum will point towards the southwest direction because the player is moving from north to west. According to Newton's second law, the force acting on the player is in the direction of the change in momentum.
Hint: The direction of the force is always in the direction of the change in momentum.
Conclusion
The force that acts on the player as they turn from north to west is directed towards the southwest.
Final Answer: The force that acts on the player is directed southwest.
The hockey player is initially moving northward. We can represent this direction as a vector pointing upwards on a graph. When the player turns westward, the direction changes to the left on the graph.
Let’s denote the initial momentum of the player moving northward as P1 and the final momentum when the player turns westward as P2. Since the speed remains the same, the magnitudes of these momentum vectors will be equal, but their directions will differ.
Draw a diagram where:
- The vector P1 points north (upward).
- The vector P2 points west (to the left).
This creates a right-angled triangle where the change in momentum can be visualized.
The change in momentum ΔP can be calculated as:
ΔP=P2−P1
Since the player is changing direction, the resultant vector will be diagonal, pointing southwest.
The resultant change in momentum will point towards the southwest direction because the player is moving from north to west. According to Newton's second law, the force acting on the player is in the direction of the change in momentum.
The force that acts on the player as they turn from north to west is directed towards the southwest.
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Match the columns
Explore 7 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Medical entrances gallery
Explore 39 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Check point 5.4
Explore 20 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A particle of mass m moving eastward with a velocity V collides with another particle of same mass moving northwards with the same speed V. The two particles coalesce and the new particle moves in NE direction. Calculate magnitude and direction of velocity of new particle.
View SolutionA cricket baal of mass 0.25 kg with speed 10 m/s collides with a bat and returns with same speed with in 0.01 s. The force acted on bat is
View SolutionAn electric current I enters and leaves a uniform circular wire of radius a through diametrically opposite points. A charged paricle q moving along the axis of the circular wire passes through its centre at speed v. The magnetic force acting on the particle when it passes through the centre has a magnitude
View SolutionAn electric current I enters and leaves a uniform circular wire of radius a through diametrically opposite points. A charged paricle q moving along the axis of the circular wire passes through its centre at speed v. The magnetic force acting on the particle when it passes through the centre has a magnitude
View SolutionAn object of mass 10kg moves at a constant speed of 10 ms−1. A constant force, that acts for 4 sec on the object, gives it a speed of 2ms−1 in opposite direction. The force acting on the object is :
View SolutionA player catches a ball of 200 gm moving with a speed of 20 m/s. if the time taken to complete the cathc is 0.5s, the force exerted on the player, hand is :-
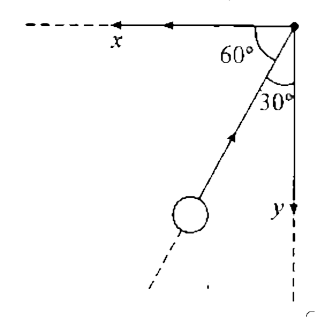
View SolutionA hockey player receives a corner shot at a speed of 15m/s at an angle of 30∘ with the y-axis and then shoots the ball along the x-axis with a speed of 30m/s If the mass of the ball is 150gm and it remains in contact with the hockey stick for 0.01s, the force imparted to the ball in the x-direction is :
View SolutionAssertion : Particle A is moving Eastwards and particle B Northwards with same speed. Then, velocity of A with respect to B is in South-East direction.
Reason : Relative velocity between them is zero as their speeds are same.
View SolutionThe coach throws a baseball to a player with an initial speed of 20m/s at an angle of 45∘ with the horizontal. At the moment the ball is thrown, the player is 50 m from the coach. At what speed and in what direction must the player run to catch the ball at the same height at which it was released? (g=10m/s2).
View SolutionA violin player riding on a slow train plays a 440 Hz note. Another violin player standing near the track plays the same note. When the two are close by and the train approaches the person on the ground, he hears 4'0 beats per second. The speed of sound in air=340ms−1 (a) Calculate the speed of the train. (b) What beat frequency is heard by the player in the train ?
View Solution