Two boys are standing at the ends A and B of a ground where AB = a. The boy at B starts running in a direction perpendicular to AB with velocity v1 . The boy at A starts running simultaneously with velocity v and catches the other in a time t, where t is
a/√υ2+υ21
√a2/(υ2−υ21)
a/(υ−υ1)
a/(υ+υ1)
The correct Answer is:B
Let two boys meet at point C after time 't' from the starting. Then AC=ut,BC=υ1t (see figure)
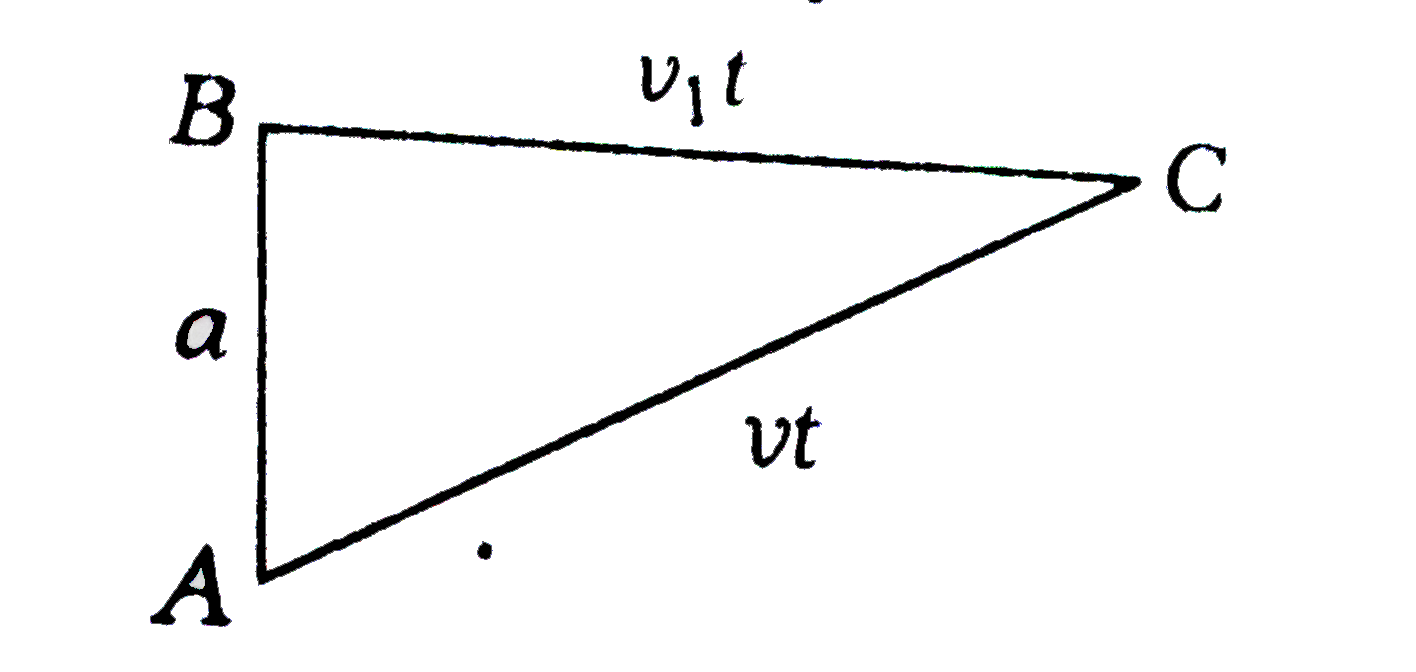
(AC)2=(AB)2+(BC)2⇒υ2t2=a2+υ21t2
By solving, we get t=√a2υ2−υ21
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Assertion and reason)
19 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Mathch the columns)
6 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.7
15 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
Two boys are standing at the ends A and B of a ground where AB = a. The boy at B starts running in a direction perpendicular to AB with velocity v1 . The boy at A starts running simultaneously with velocity v and catches the other in a time t, where t is
View SolutionA conducting rod AB of length l is projected on a frictionless frame PSRQ with velocity v0 at any instant. The velocity of the rod after time t is
View Solution
Knowledge Check
Four children are standing at the corners A, B, C and D of a square of side l. They simultaneously start running such that A runs towards B, B towaards C, C runs towards D and D runs towards A, each with a velocity v.They will meet after a time
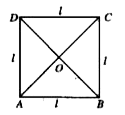 A√2l/vBl/vCl/√2vD4l/v
A√2l/vBl/vCl/√2vD4l/v
A boy is running along positive x - axis with 9m/s. While running he manages to throw a stone in a plane perpendicular to his direction of running with velocity 12m/s at an angle 30∘ with vertical. Find the speed of the stone at the highest point of the trajectory.
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
View SolutionA man of 50kg is standing at one end on a boat of length 25m and mass 200kg.If he starts running and when he reaches the other end, has a velocity 2ms−1 with respect to the boat.The final velocity of the boat is
View SolutionA man of 50kg is standing at one end on a boat of length 25m and mass 200kg.If he starts running and when he reaches the other end, has a velocity 2ms−1 with respect to the boat.The final velocity of the boat is
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
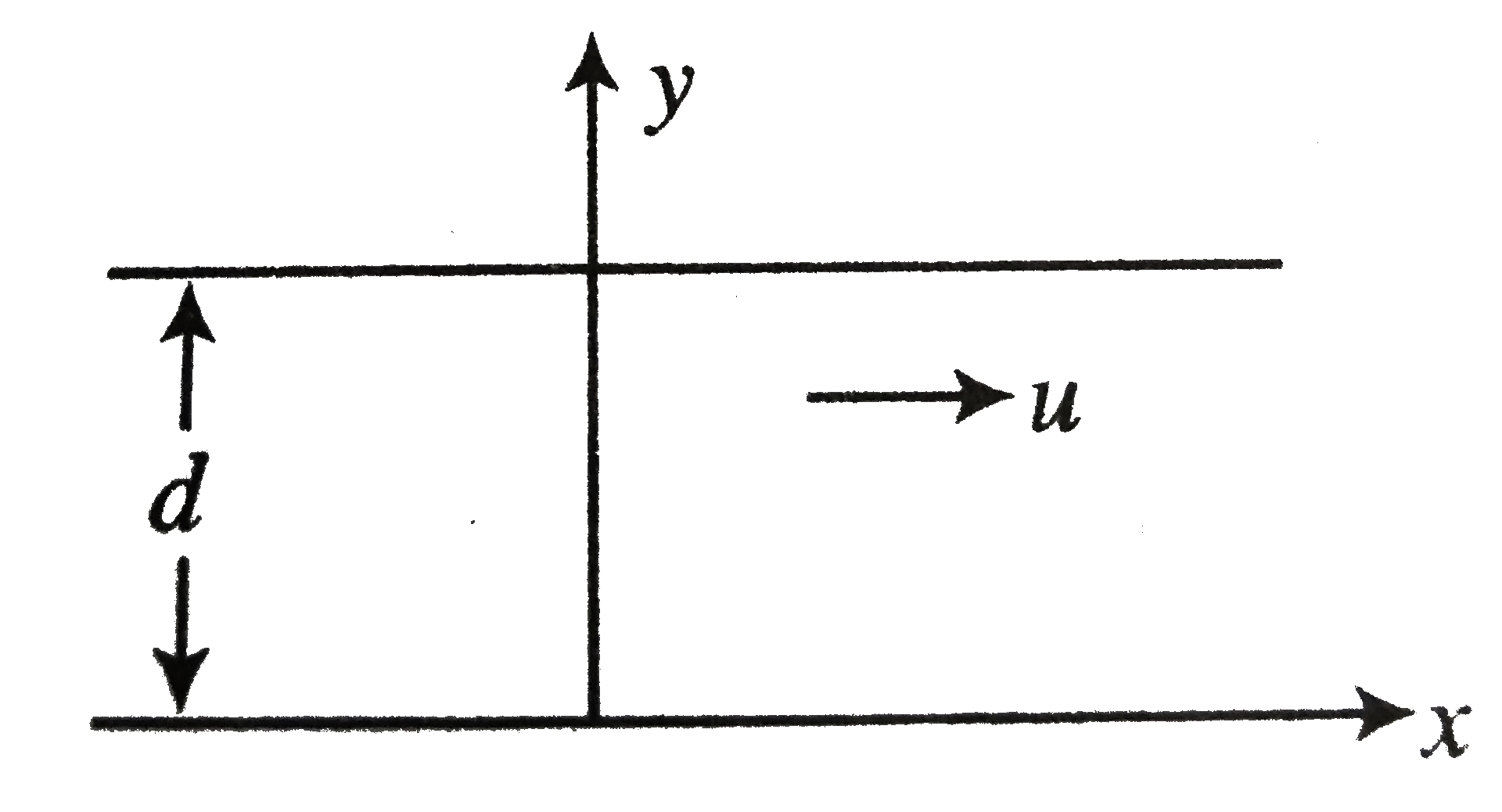
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units. Find time taken by him to across the river.
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
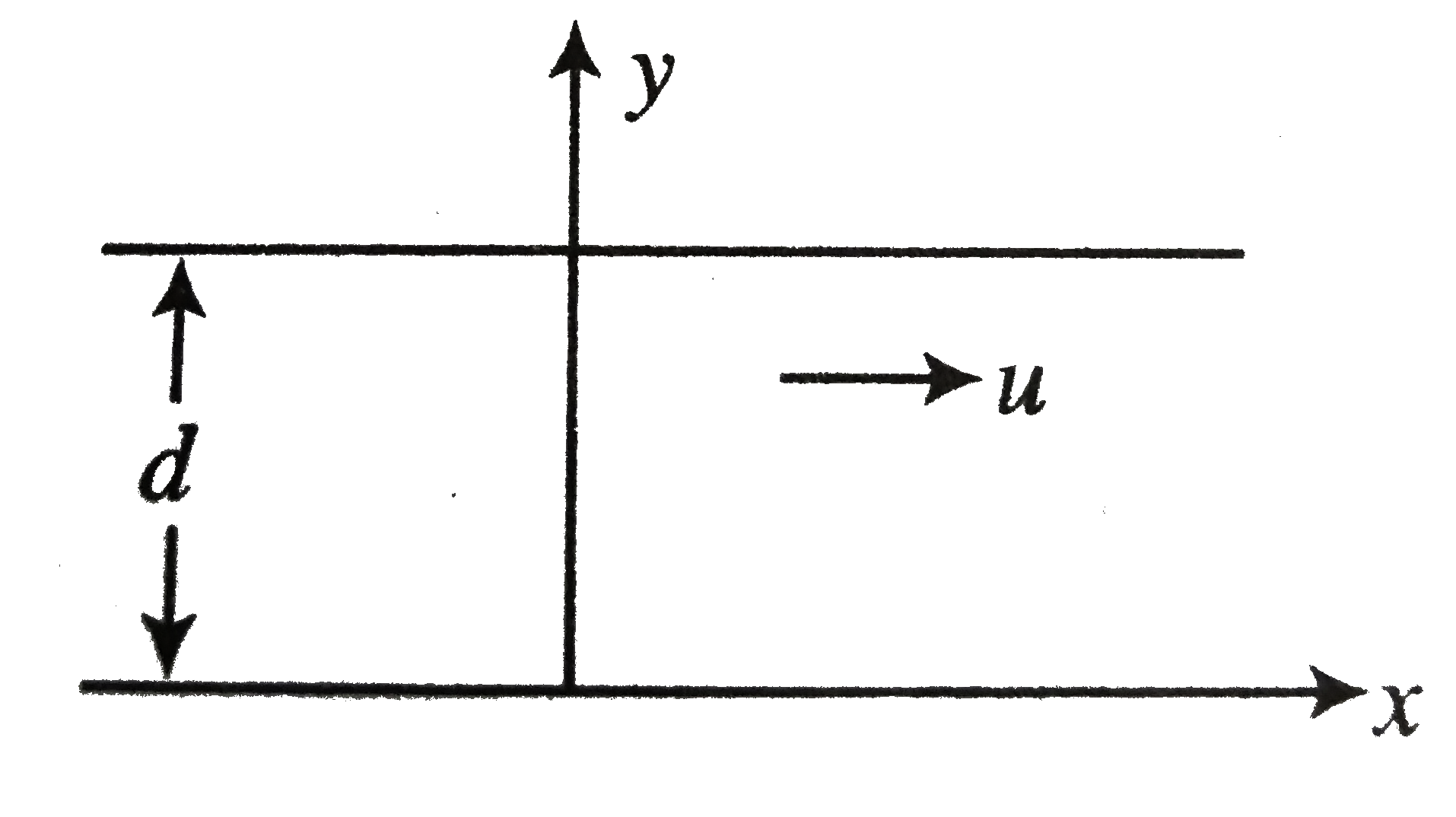
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
View Solution
