A body travelling with uniform acceleration crosses two point A and B with velocities 20ms−1 and 30ms−1 respectively. The speed of the body at the mid-point of A and B is.
25ms−1
25.5ms−1
24ms−1
10√6ms−1
The correct Answer is:B
To solve the problem step by step, we can follow these steps:
Step 1: Understand the Problem
We have a body moving with uniform acceleration that passes two points A and B with velocities vA=20m/s and vB=30m/s respectively. We need to find the speed of the body at the midpoint C between A and B.
Step 2: Define the Midpoint
Let the distance between points A and B be 2s. Therefore, the distance from A to C (midpoint) is s and from C to B is also s.
Step 3: Apply the Equation of Motion
Using the equation of motion:
v2B=v2A+2a⋅d
where:
- vB=30m/s
- vA=20m/s
- d=2s (the total distance from A to B)
Substituting the values:
302=202+2a⋅(2s)
900=400+4as
4as=900−400=500
as=5004=125
Step 4: Find the Velocity at Point C
Now, we will find the velocity at point C using the same equation of motion from A to C:
v2C=v2A+2a⋅s
Substituting the known values:
v2C=202+2a⋅s
We know from the previous calculation that as=125, so:
v2C=400+2⋅125
v2C=400+250=650
vC=√650
Calculating √650:
vC≈25.5m/s
Final Answer
The speed of the body at the midpoint C is approximately 25.5m/s.
---
We have a body moving with uniform acceleration that passes two points A and B with velocities vA=20m/s and vB=30m/s respectively. We need to find the speed of the body at the midpoint C between A and B.
Let the distance between points A and B be 2s. Therefore, the distance from A to C (midpoint) is s and from C to B is also s.
Using the equation of motion:
v2B=v2A+2a⋅d
where:
- vB=30m/s
- vA=20m/s
- d=2s (the total distance from A to B)
302=202+2a⋅(2s)
900=400+4as
4as=900−400=500
as=5004=125
Now, we will find the velocity at point C using the same equation of motion from A to C:
v2C=v2A+2a⋅s
Substituting the known values:
v2C=202+2a⋅s
We know from the previous calculation that as=125, so:
v2C=400+2⋅125
v2C=400+250=650
vC=√650
Calculating √650:
vC≈25.5m/s
The speed of the body at the midpoint C is approximately 25.5m/s.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.5
25 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.6
20 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.3
10 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
A car moving with constant acceleration crosses two points A and B with velocities 10 m/s and 20 m/s in its path. Find the velocity of the car midway between A and B. (in m/s).
View SolutionA body is moving with constant acceleration, a=5ms2 from A to B in straight line AB. The velocity of particle at A and B are 5 m/s and 15 m/s respectively. The velocity at mid-point of AB is
View Solution
Knowledge Check
Light travels in two media A and B with speeds 1.8×108ms–1and2.4×108ms–1 respectively. Then the critical angle between them is
Asin−1(23)Btan−1(34)Ctan−1(23)Dsin−1(34)
A particle moving with uniform acceleration from A to B along a straight line has velcities v1 and v2 at A and B respectively. If C is the mid-point between A and B then determine the velocity of the particle at C .
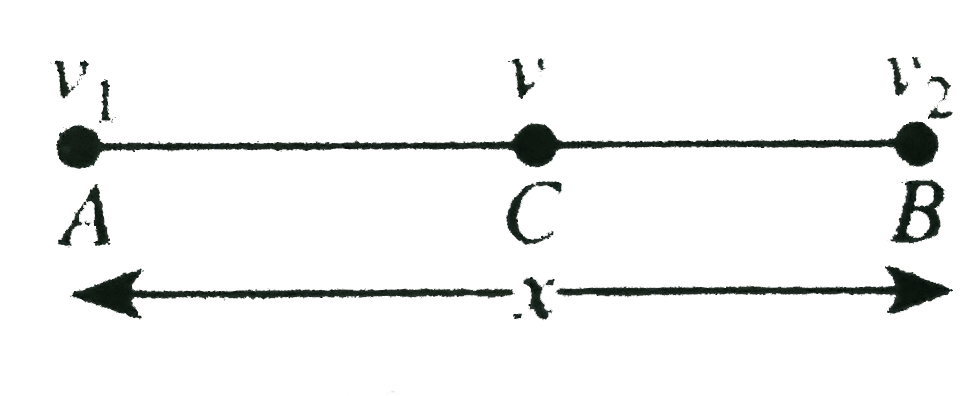 .
.
View SolutionA body is moving with uniform acceleration covers 200 m in the first 2 s and 220 m in the next 4s. Find the velocity in ms−1 after 7 s.
View SolutionA body moving with uniform acceleration travels 84 m in the first 6 s and 180 m in the next 5 s. Find : (a) the initial velocity, and (b) the acceleration of the body.
View SolutionA body moves from rest with a uniform acceleration and travels 270 m in 3 s. Find the velocity of the body at 10 s after the start.
View SolutionA body moving with uniform acceleration describes 40 m in the first 5 s and 70 m in the next 5 s.its initial velocity will be
View SolutionA particle moving with uniform acceleration passes the point x=2m with velocity 20m/s at the instant t=0. Some time later it is observed at the point x=32m moving with velocity 10m/s.
(a) What is its acceleration?
(b) Find its position nd velocity at the instant t=8s.
(c) What is the distance traveled during the interval t=0 to 8s?
View SolutionA body of mass 2kg starts from rest and moves with uniform acceleration. It acquires a velocity 20ms−1 in 4s.
The power exerted on the body at 2s is
View Solution
