A train accelerating uniormly from rest attains a maximum speed of 40ms−1 in 20s. It travels at this speed for 20s and is brought to rest with uniform retardation i further 40s. What is the average velocity during this period?
80/3ms−1
40ms−1
25ms−1
30ms−1
The correct Answer is:C
To solve the problem step by step, we will calculate the average velocity of the train during its entire journey.
Step 1: Identify the phases of motion
The train goes through three distinct phases:
1. Acceleration from rest to maximum speed (Phase 1)
2. Constant speed (Phase 2)
3. Deceleration to rest (Phase 3)
Step 2: Calculate the total time
The total time for the journey is the sum of the time for each phase:
- Time for Phase 1 (t1) = 20 seconds
- Time for Phase 2 (t2) = 20 seconds
- Time for Phase 3 (t3) = 40 seconds
Total time (T) = t1 + t2 + t3 = 20 + 20 + 40 = 80 seconds
Step 3: Calculate the displacement for each phase
Phase 1: Acceleration
- Initial velocity (u) = 0 m/s
- Final velocity (v) = 40 m/s
- Time (t1) = 20 s
Using the formula for acceleration:
v=u+at
40=0+a⋅20
a=4020=2m/s2
Now, calculate the displacement (S1) during this phase using:
S=ut+12at2
S1=0⋅20+12⋅2⋅(20)2
S1=0+12⋅2⋅400
S1=400meters
Phase 2: Constant Speed
- Speed = 40 m/s
- Time (t2) = 20 s
Displacement (S2) during this phase:
S2=speed⋅time
S2=40⋅20=800meters
Phase 3: Deceleration
- Initial velocity (u) = 40 m/s
- Final velocity (v) = 0 m/s
- Time (t3) = 40 s
Using the formula for deceleration:
v=u+at
0=40+a⋅40
a=−4040=−1m/s2
Now, calculate the displacement (S3) during this phase:
S3=ut+12at2
S3=40⋅40+12⋅(−1)⋅(40)2
S3=1600−12⋅1600
S3=1600−800=800meters
Step 4: Calculate total displacement
Total displacement (S) = S1 + S2 + S3
S=400+800+800=2000meters
Step 5: Calculate average velocity
Average velocity (V_avg) is given by:
Vavg=Total DisplacementTotal Time
Vavg=200080=25m/s
Final Answer
The average velocity of the train during this period is 25 m/s.
---
The train goes through three distinct phases:
1. Acceleration from rest to maximum speed (Phase 1)
2. Constant speed (Phase 2)
3. Deceleration to rest (Phase 3)
The total time for the journey is the sum of the time for each phase:
- Time for Phase 1 (t1) = 20 seconds
- Time for Phase 2 (t2) = 20 seconds
- Time for Phase 3 (t3) = 40 seconds
- Initial velocity (u) = 0 m/s
- Final velocity (v) = 40 m/s
- Time (t1) = 20 s
v=u+at
40=0+a⋅20
a=4020=2m/s2
S=ut+12at2
S1=0⋅20+12⋅2⋅(20)2
S1=0+12⋅2⋅400
S1=400meters
- Speed = 40 m/s
- Time (t2) = 20 s
S2=speed⋅time
S2=40⋅20=800meters
- Initial velocity (u) = 40 m/s
- Final velocity (v) = 0 m/s
- Time (t3) = 40 s
v=u+at
0=40+a⋅40
a=−4040=−1m/s2
S3=ut+12at2
S3=40⋅40+12⋅(−1)⋅(40)2
S3=1600−12⋅1600
S3=1600−800=800meters
Total displacement (S) = S1 + S2 + S3
S=400+800+800=2000meters
Average velocity (V_avg) is given by:
Vavg=Total DisplacementTotal Time
Vavg=200080=25m/s
The average velocity of the train during this period is 25 m/s.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.5
25 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.6
20 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.3
10 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
Knowledge Check
A train starting from rest, and moving with uniform acceleration α, acquires a speed v. Then its comes to a stop with uniform retardation β. Then the average velocity of the train is
Av/2Bv/4C(α+β)t/2D(α+β)t/αβ
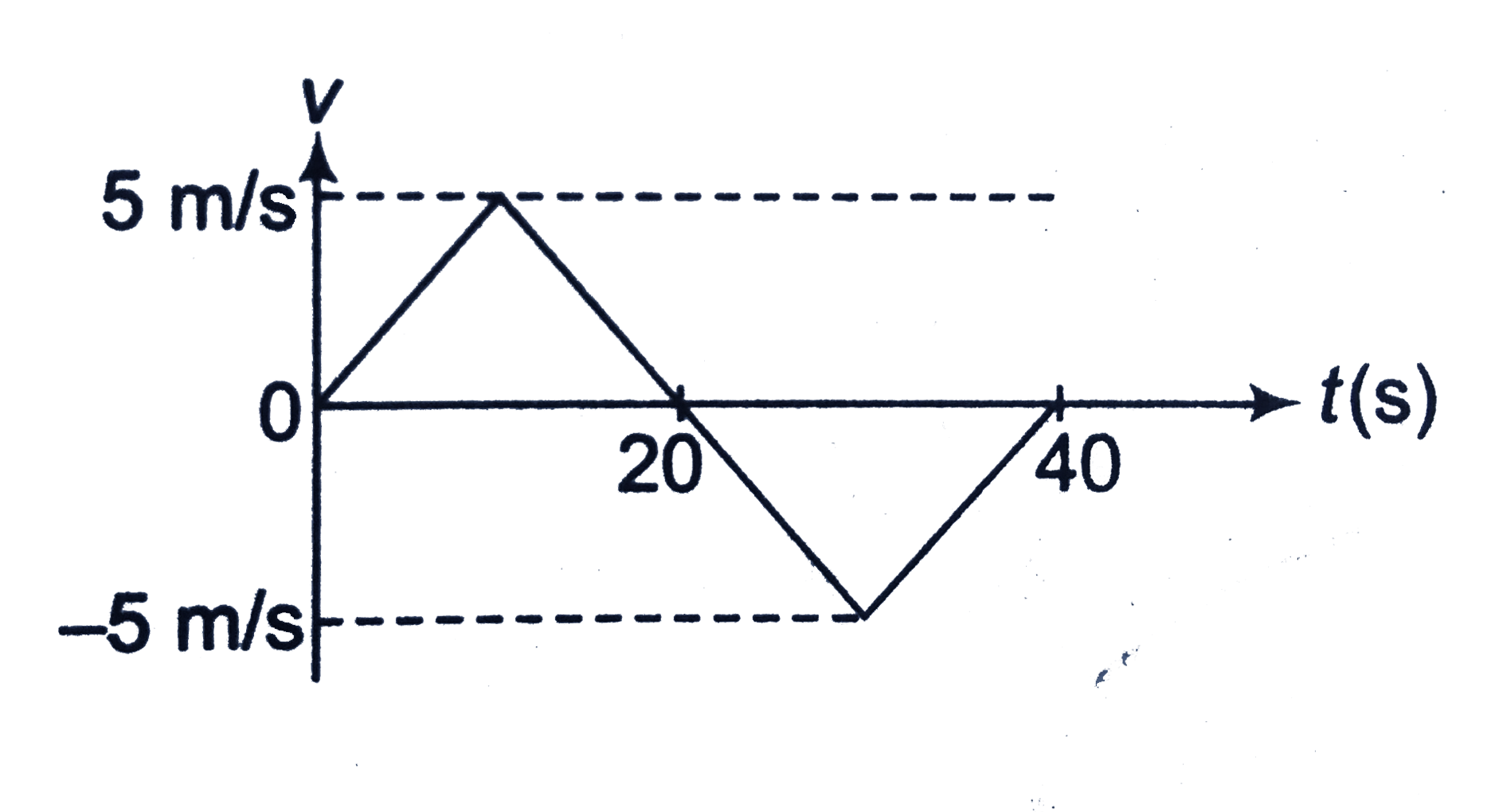
From the velocity-time plot shown in Fig. find the distance travelled by the particle during the first 40s. Also find the average velocity during this period.
View SolutionA train starts from rest and accelerates uniformly at a rate of 2 m s−2 for 10 s. It then maintains a constant speed for 200 s. The brakes are then applied and the train is uniformly retarded and comes to rest in 50 s. Find : (i) the maximum velocity reached, (ii) the retardation in the last 50 S, (iii) the total distance travelled, and (iv) the average velocity of the train.
View SolutionA block of mass 10 kg accelerates uniformly from rest to a speed of 2 m/s in 20 sec. The average power developed in time interval of 0 to 20 sec is
View SolutionA car starts form rest and accelerates uniformly for 10s to a velocity of 8ms−1. It then runs at a constant velocity an dis finally brought to rest in 64m with a constant retardation. The totla distance covered by the car is 584m Find the value of acceleration, retardation, and totl time taken.
View SolutionA train goes from rest to rest between two stations with uniform acceleration and retardation. Find the rato of maximum velocity of the average velocity.
View SolutionIf a car at rest, accelerates uniformly to a speed of 144km/h in 20s, it covers a distance of
View SolutionA train is moving at a velocity of 25ms−1. If it is brought to rest by applying the brakes which produces a uniform retardation of 0.5ms−2. Calculate velocity of the train after 10s.
View Solution
