Three identical metal rods A, B and C are placed end to end and a temperature difference is maintained between the free ends of A and C. If the thermal conductivity of B(KB) is thrice that of C(KC) and half that of A(KA), (KA=49w/mK) calculate the effective thermal conductivity of the system ?
13KA
3KA
2KA
23KA
The correct Answer is:A
To solve the problem, we need to calculate the effective thermal conductivity of three identical metal rods A, B, and C placed end to end, given their thermal conductivities and the relationships between them.
1. Identify the Given Values:
- Thermal conductivity of rod A, KA=49W/mK
- Thermal conductivity of rod B, KB=12KA=12×49=24.5W/mK
- Thermal conductivity of rod C, KC=13KB=13×24.5=8.17W/mK
2. Calculate the Thermal Resistances:
- The thermal resistance R for each rod is given by the formula:
R=LK⋅A
- Since the rods are identical in length L and cross-sectional area A, we can express the resistances as:
RA=LKA⋅A,RB=LKB⋅A,RC=LKC⋅A
3. Substituting the Values:
- Substitute the values of KA, KB, and KC:
RA=L49⋅A,RB=L24.5⋅A,RC=L8.17⋅A
4. Calculate the Total Thermal Resistance:
- The total thermal resistance Rtotal for the series combination is:
Rtotal=RA+RB+RC=L49⋅A+L24.5⋅A+L8.17⋅A
- Factor out LA:
Rtotal=LA(149+124.5+18.17)
5. Calculate Each Resistance Value:
- Calculate the individual resistance values:
149≈0.0204,124.5≈0.0408,18.17≈0.122
- Sum these values:
149+124.5+18.17≈0.0204+0.0408+0.122≈0.1832
6. Calculate the Effective Thermal Conductivity:
- The effective thermal conductivity Keff can be found using the formula:
Keff=LRtotal⋅A⋅3L=1Rtotal⋅3
- Thus:
Keff=1(LA⋅0.1832)⋅3=KA3=493≈16.33W/mK
Final Answer:
The effective thermal conductivity of the system is approximately Keff≈16.33W/mK.
- Thermal conductivity of rod A, KA=49W/mK
- Thermal conductivity of rod B, KB=12KA=12×49=24.5W/mK
- Thermal conductivity of rod C, KC=13KB=13×24.5=8.17W/mK
- The thermal resistance R for each rod is given by the formula:
R=LK⋅A
- Since the rods are identical in length L and cross-sectional area A, we can express the resistances as:
RA=LKA⋅A,RB=LKB⋅A,RC=LKC⋅A
- Substitute the values of KA, KB, and KC:
RA=L49⋅A,RB=L24.5⋅A,RC=L8.17⋅A
- The total thermal resistance Rtotal for the series combination is:
Rtotal=RA+RB+RC=L49⋅A+L24.5⋅A+L8.17⋅A
- Factor out LA:
Rtotal=LA(149+124.5+18.17)
- Calculate the individual resistance values:
149≈0.0204,124.5≈0.0408,18.17≈0.122
- Sum these values:
149+124.5+18.17≈0.0204+0.0408+0.122≈0.1832
- The effective thermal conductivity Keff can be found using the formula:
Keff=LRtotal⋅A⋅3L=1Rtotal⋅3
- Thus:
Keff=1(LA⋅0.1832)⋅3=KA3=493≈16.33W/mK
The effective thermal conductivity of the system is approximately Keff≈16.33W/mK.
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Assertion and reason
17 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Match the columns
4 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check points 16.4
29 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
Two identical metal rods A and B are joined end to end. The free end of A is kept at 27°C and the free end of B at 37°C. Calculate the temperature of the interface. Thermal conductivity of A=385Wm−1K−1, that of B 110Wm−1K−1.
View SolutionTwo metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
View SolutionThree identical rods have been joined at a junction to make it a Y shape structure .If two free ends are maintained at 60∘C and the thired end is at 0∘C then what is the juction temperature θ?
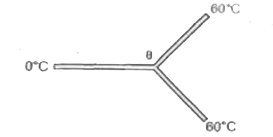
View Solution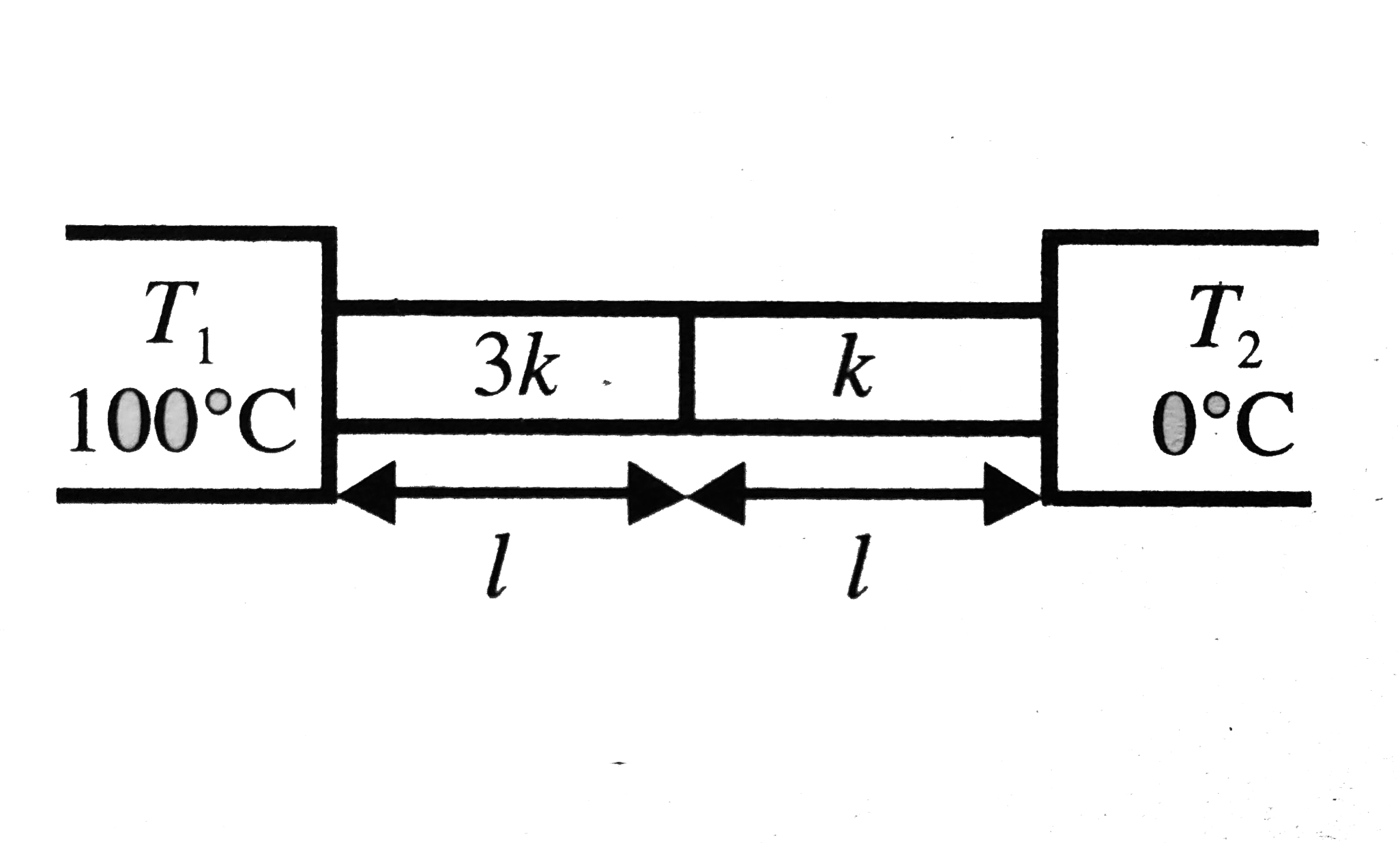
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View SolutionTwo rods A and B of same area of cross-section are joined together end to end The free end of the rod A is kept in melting ice at 300 K and free end of B rod at 400 K. The rods are of the same length. The conductivity of A is 3 times that of B. Calculate the temperature of the junction of the rods.
View SolutionTwo metal rods 1 and 2 of the same length have same temperature difference between their ends. Their thermal conductivities are K1andK2 and cross-section areas A1andA2 respectively. What is the required condition for the same rate of heat conduction in them?
View SolutionThree identical rods have been joined at a junction to make it a Y shape structure. If two free ends are maintained at 45∘C and the end is at 0∘C, then what is the junction temperature T?

View SolutionTwo rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be

View SolutionThree rods of same dimension are joined in series having thermal conductivity k1 , k2 and k3. The equivalent thermal conductivity is
View SolutionA cylinder of radius r made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius r and outer radius 2r made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. Show that the effective thermal conductivity of the system is (K1+3K2)/4.
View Solution
