Sunrays are allowed to fall on a lens of diameter 20 cm. They are then brought to focus on a calorimeter containing 20 g of ice. If the absorption by the lens is neglible, the time required to melt all the ice is
(solar constant =1.9cal−1mincm−2andL=80calg−1)
6.4 min
3.2 min
7.2 min
2.7 min
The correct Answer is:D
To solve the problem step by step, we will follow the given information and apply the relevant formulas.
Step 1: Calculate the heat required to melt the ice
The heat required (Q) to melt the ice can be calculated using the formula:
Q=m×L
where:
- m = mass of ice = 20 g
- L = latent heat of fusion of ice = 80 cal/g
Substituting the values:
Q=20g×80cal/g=1600cal
Step 2: Calculate the area of the lens
The area (A) of the lens can be calculated using the formula for the area of a circle:
A=π(D2)2
where:
- D = diameter of the lens = 20 cm
Substituting the value:
A=π(202)2=π×102=100πcm2
Step 3: Calculate the power incident on the lens
The power (P) incident on the lens can be calculated using the solar constant and the area:
P=solar constant×A
Given the solar constant = 1.9 cal/min/cm², we have:
P=1.9cal/min/cm2×100πcm2
Using π≈3.14:
P≈1.9×100×3.14≈597cal/min
Step 4: Calculate the time required to melt the ice
The time (T) required to melt the ice can be calculated using the formula:
T=QP
Substituting the values:
T=1600cal597cal/min≈2.68min
Step 5: Final result
Rounding off the result, the time required to melt all the ice is approximately:
T≈2.7min
Summary
The time required to melt all the ice is approximately 2.7 minutes.
---
Q=m×L
where:
- m = mass of ice = 20 g
- L = latent heat of fusion of ice = 80 cal/g
Q=20g×80cal/g=1600cal
A=π(D2)2
where:
- D = diameter of the lens = 20 cm
A=π(202)2=π×102=100πcm2
P=solar constant×A
Given the solar constant = 1.9 cal/min/cm², we have:
P=1.9cal/min/cm2×100πcm2
Using π≈3.14:
P≈1.9×100×3.14≈597cal/min
T=QP
Substituting the values:
T=1600cal597cal/min≈2.68min
T≈2.7min
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY AND HEAT TRANSFERExercise:Assertion and reason
Explore 17 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY AND HEAT TRANSFERExercise:Match the columns
Explore 4 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY AND HEAT TRANSFERExercise:Check points 16.4
Explore 29 Videos
- CALORIMETRY & HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY & HEAT TRANSFERExercise:Level 2 Subjective
Explore 14 Videos
- CENTRE OF MASSBook:DC PANDEY ENGLISHChapter:CENTRE OF MASSExercise:Medical entrances gallery
Explore 27 Videos
Similar Questions
Knowledge Check
Rays from the sun ar focuseed by a lens of diameter 5 cm on to a block of ice and 10 g of ice is melted in 20 min. Therefore the heat from the sun reaching the earth per min per square centrimetre is
(Latent heat of ice L=80calg−1)A2.04calB0.51calC4.08calD3.02calOne end of a 0.25 m long metal bar is in steam and the other is in contact with ice . If 12 g of ice melts per minute, what is the thermal conductivity of the metal? Given cross-section of the bar =5×10−4m2 and latent heat of ice is 80calg−1
A20cals−1m−1.∘C−1B10cals−1m−1.∘C−1C40cals−1m−1.∘C−1D80cals−1m−1.∘C−1
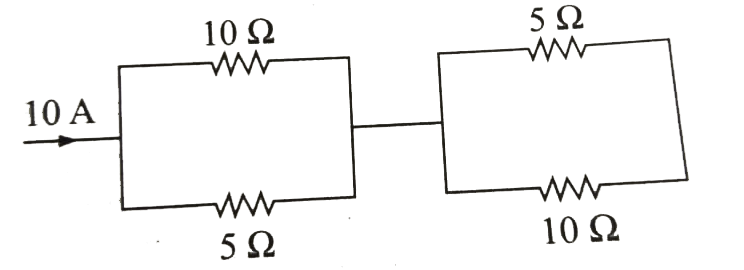
Four resistances carrying a current shown in Fig. 7.41 are immersed in a box containing ice at 0∘C. How much ice must be put in the box every 10min to keep the average quantity of ice in the box constant? Latent heat of ice is 80calg−1.
View Solution19 g of water at 30∘C and 5 g of ice at −20∘C are mixed together in a calorimeter. What is the final temperature of the mixture? Given specific heat of ice =0.5calg−1(.∘C)−1 and latent heat of fusion of ice =80calg−1
View SolutionBottom of a lake is at 0∘C and atmospheric temperature is −20∘C. If 1 cm ice is formed on the surface in 24 h, then time taken to form next 1 cm of ice is
View Solution5 g of water at 30∘C and 5 g of ice at −20∘C are mixed together in a calorimeter Find the final temperature of the mixure. Assume water equivalent of calorimeter to be negligible, sp. Heats of ice and water are 0.5 and 1cal/gC∘, and latent heat of ice is 80cal/g
View SolutionEarth receives 1400W/m2 of solar power. If all the solar energy falling on a lens of area 0.2m2 is focused on to a block of ice of mass 280 grams, the time taken to melt the ice will be….. Minutes. (Latent heat of fusion of ice=3.3×105J/kg)
View SolutionEarth receives 1400W/m2 of solar power. If all the solar energy falling on a lens of area 0.2m2 is focused on to a block of ice of mass 280 grams, the time taken to melt the ice will be….. Minutes. (Latent heat of fusion of ice=3.3×105J/kg.)
View Solution

