A solid sphere rolls without slipping and presses a spring of spring constant k as shown in figure. Then, the compression in the spring will be
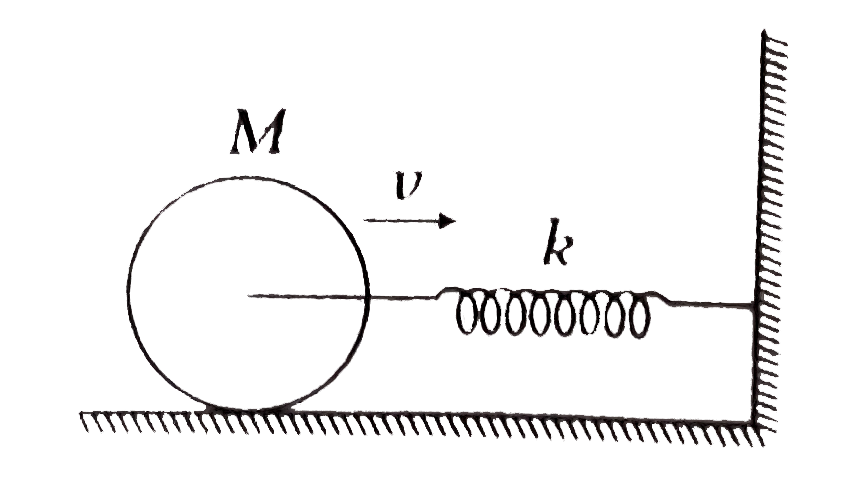
v√2M3k
v√2M5k
v√5k7M
v√7M5k
The correct Answer is:D
In case of pure rolling, ratio of rotational to translational kinetic energy is 2/5. Therefore, total kinetic energy is 7/5 times the translational kinetic energy. At maximum compression, whole of energy is elastic potential. Hence,
75(12Mv2)=12kx2max
∴ The compression of the spring, xmax=v√7M5k.
Topper's Solved these Questions
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(B) Chapter Exercises
Explore 25 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:Check point 9.3
Explore 15 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Integer type q.
Explore 14 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
Similar Questions
A 1 Kg solid sphere rolls without slipping on a rough horizontal suface as shown in figure. Select incorrect alternative

View SolutionA block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?

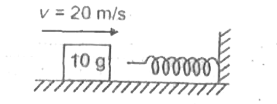
View SolutionA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
View SolutionThe electrical analog of a spring constant k is
View SolutionA solid ball of mass m is made to fail from a height H on a pan suspended through a spring of spring constant K as shown in figure. If the does not rebound and the pan is massless, then amplitude of oscillation is
View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:

View SolutionA spring of spring constant k is cut in three equal pieces. The spring constant of each part will be
View SolutionA block of mass 20 kg is hung with the help of ideal string, pulleys and spring (Spring constant k = 1000 N/m) as shown in figure. If block is in equilibrium position then extension in the spring will be (g=10ms−2)
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)

View Solution
