By which curve will be variation of gravitational potential of a hollow sphere of radius R with distance be depicted ?

The correct Answer is:C
To determine the variation of gravitational potential V of a hollow sphere of radius R with distance r, we can analyze the gravitational potential in different regions relative to the hollow sphere.
1. Understanding the Hollow Sphere:
- A hollow sphere is a spherical shell with mass distributed uniformly over its surface. The gravitational field inside a hollow sphere is zero.
2. Gravitational Potential Inside the Hollow Sphere:
- Since the gravitational field g inside the hollow sphere is zero, the gravitational potential V remains constant throughout the interior of the sphere.
- Let’s denote the gravitational potential at the surface of the sphere (radius R) as V(R).
3. Calculating Gravitational Potential at the Surface:
- The gravitational potential V at the surface of the hollow sphere can be calculated using the formula:
V(R)=−GMR
- Here, G is the universal gravitational constant and M is the mass of the hollow sphere.
4. Gravitational Potential Outside the Hollow Sphere:
- For points outside the hollow sphere (where r>R), the gravitational potential can be expressed as:
V(r)=−GMr
- This shows that the potential decreases as we move further away from the sphere.
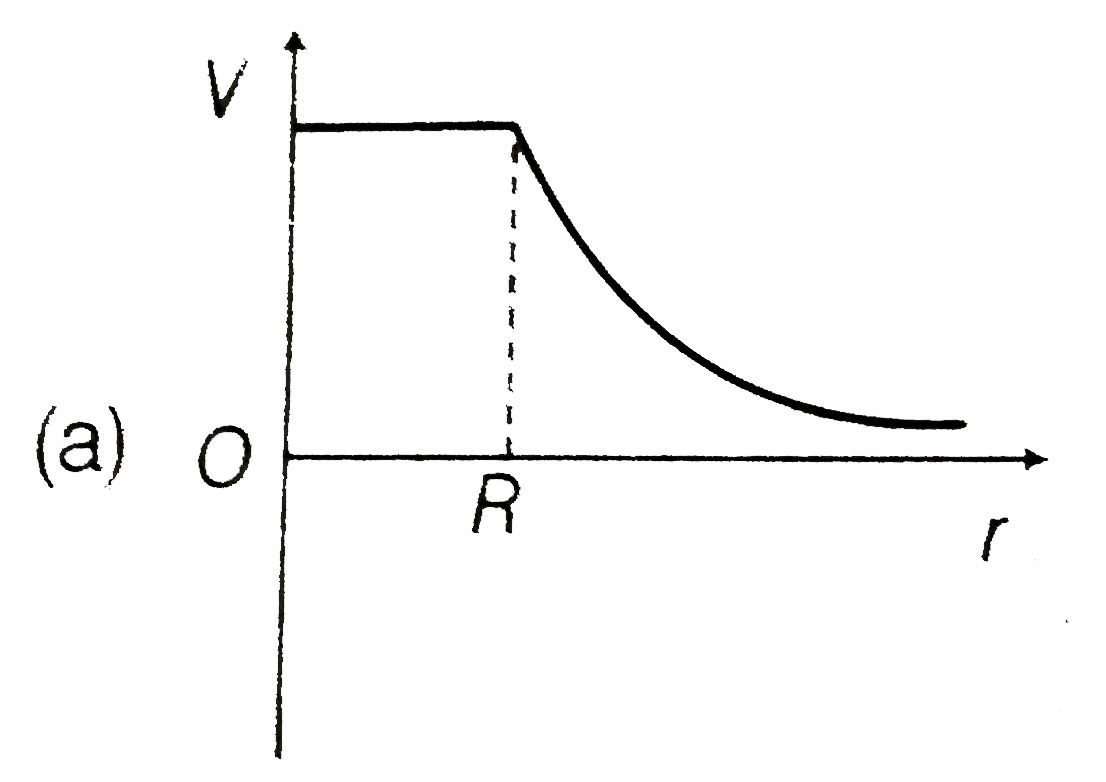
5. Graphing the Variation of Gravitational Potential:
- On a graph where the x-axis represents the distance r and the y-axis represents the gravitational potential V:
- From r=0 to r=R, the potential V remains constant at −GMR.
- At r=R, the potential starts decreasing as −GMr for r>R.
- The graph will show a horizontal line at V=−GMR until r=R, and then it will curve downward as r increases.
6. Conclusion:
- The variation of gravitational potential of a hollow sphere with distance is depicted by a graph that is constant for r<R and decreases for r>R.
- A hollow sphere is a spherical shell with mass distributed uniformly over its surface. The gravitational field inside a hollow sphere is zero.
- Since the gravitational field g inside the hollow sphere is zero, the gravitational potential V remains constant throughout the interior of the sphere.
- Let’s denote the gravitational potential at the surface of the sphere (radius R) as V(R).
- The gravitational potential V at the surface of the hollow sphere can be calculated using the formula:
V(R)=−GMR
- Here, G is the universal gravitational constant and M is the mass of the hollow sphere.
- For points outside the hollow sphere (where r>R), the gravitational potential can be expressed as:
V(r)=−GMr
- This shows that the potential decreases as we move further away from the sphere.
- On a graph where the x-axis represents the distance r and the y-axis represents the gravitational potential V:
- From r=0 to r=R, the potential V remains constant at −GMR.
- At r=R, the potential starts decreasing as −GMr for r>R.
- The graph will show a horizontal line at V=−GMR until r=R, and then it will curve downward as r increases.
- The variation of gravitational potential of a hollow sphere with distance is depicted by a graph that is constant for r<R and decreases for r>R.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.4
10 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.5
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.2
20 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Find the radius of gyration of a hollow uniform sphere of radius R about its tangent.
View SolutionThe diagram showing the variation of gravitational potential of earth with distance from the centre of earth is
View SolutionThe radius of gyration of a hollow sphere of radius R about an axis along its tangent is
View SolutionThe gravitational potential at a point outside the solid sphere of radius "R" and at a distance of "r" will be :
View SolutionThe correct variation of gravitational potential V with radius r measured from the centre of earth of radius R is given by
View SolutionElectric potential at a point P, r distance away due to a point charge q kept at point A is V. If twice of this charge is distributed uniformly on the surface of a hollow sphere of radius 4r with centre at point A the potential at P now is
View SolutionFollowing curve shows the variation of intesity of gravitational field (→I) with distance from the centre of solid sphere(r) :
View SolutionWater from a tap, maintained at a costant potential V, is allolwed to fall by drops of radius r through a small hole into a hollow conducting sphere of radius R standing on an insulating stand until it fills the entire sphere. Find the potential of the hollow conductor after it is completely filled with water.
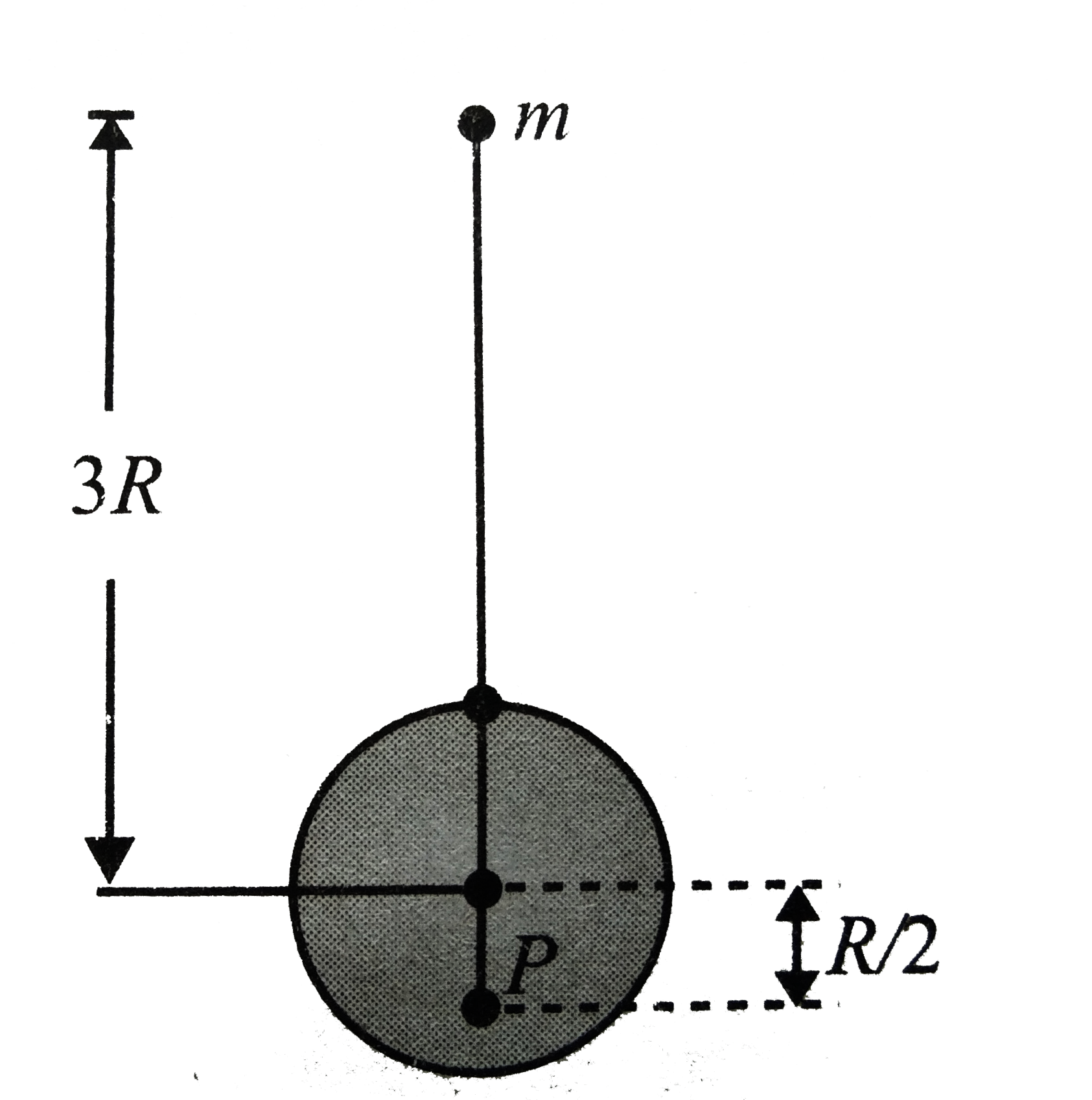
View SolutionA point mass m is released from rest at a distance of 3R from the centre of a thin-walled hollow sphere of radius R and mass M as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point P at a distance R/2 from the centre of the sphere is
View SolutionIf a solid and a hollow conducting sphere have same radius then
View Solution
