The diagram showing the variation of gravitational potential of earth with distance from the centre of earth is
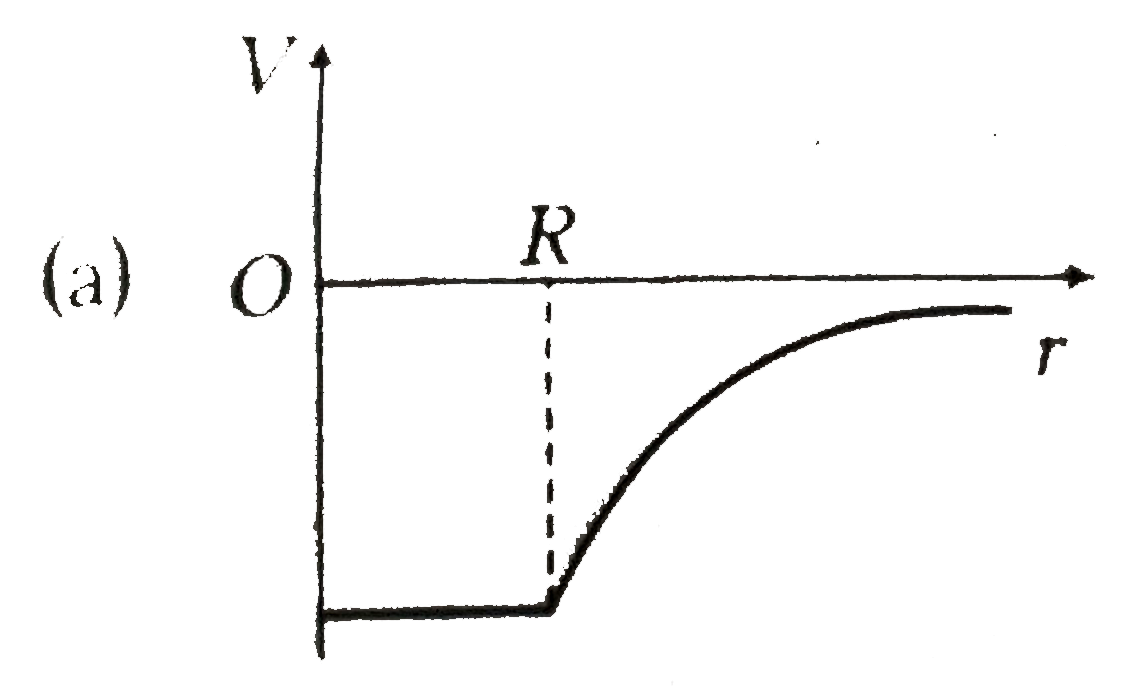


The correct Answer is:C
To solve the question regarding the variation of gravitational potential of Earth with distance from the center of Earth, we will analyze the gravitational potential both inside and outside the Earth.
1. Understanding Gravitational Potential:
Gravitational potential (V) is defined as the work done per unit mass to bring a mass from infinity to a point in the gravitational field. It is given by the formula:
V=−GMr
where G is the gravitational constant, M is the mass of the Earth, and r is the distance from the center of the Earth.
2. Inside the Earth (r < R):
When we are inside the Earth (at a distance r from the center where r<R), only the mass enclosed within that radius contributes to the gravitational potential. The gravitational potential inside a uniform sphere is given by:
V=−GM2R+GMR3r2
where R is the radius of the Earth. This equation shows that the potential increases quadratically with distance r from the center.
3. At the Surface of the Earth (r = R):
At the surface of the Earth, we can substitute r=R into the equation for the potential:
V=−GMR
This is the gravitational potential at the surface.
4. Outside the Earth (r > R):
For distances greater than the radius of the Earth, the Earth can be treated as a point mass located at its center. Thus, the gravitational potential is again given by:
V=−GMr
This shows that the potential decreases inversely with distance r.
5. Plotting the Graph:
- For r<R: The potential increases from −3GM2R (at the center) to −GMR (at the surface).
- For r=R: The value is −GMR.
- For r>R: The potential decreases towards zero as r increases.
6. Conclusion:
The graph of gravitational potential versus distance from the center of the Earth will show a parabolic increase for r<R and a hyperbolic decrease for r>R. The correct representation of this variation is depicted in option (T).
Gravitational potential (V) is defined as the work done per unit mass to bring a mass from infinity to a point in the gravitational field. It is given by the formula:
V=−GMr
where G is the gravitational constant, M is the mass of the Earth, and r is the distance from the center of the Earth.
When we are inside the Earth (at a distance r from the center where r<R), only the mass enclosed within that radius contributes to the gravitational potential. The gravitational potential inside a uniform sphere is given by:
V=−GM2R+GMR3r2
where R is the radius of the Earth. This equation shows that the potential increases quadratically with distance r from the center.
At the surface of the Earth, we can substitute r=R into the equation for the potential:
V=−GMR
This is the gravitational potential at the surface.
For distances greater than the radius of the Earth, the Earth can be treated as a point mass located at its center. Thus, the gravitational potential is again given by:
V=−GMr
This shows that the potential decreases inversely with distance r.
- For r<R: The potential increases from −3GM2R (at the center) to −GMR (at the surface).
- For r=R: The value is −GMR.
- For r>R: The potential decreases towards zero as r increases.
The graph of gravitational potential versus distance from the center of the Earth will show a parabolic increase for r<R and a hyperbolic decrease for r>R. The correct representation of this variation is depicted in option (T).
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:Check Point 10.4
Explore 10 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:Check Point 10.5
Explore 20 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:Check Point 10.2
Explore 20 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 10 Videos
Similar Questions
Knowledge Check
A particle of mass M is placed at the centre of a spherical shell of same mass and radius a. What will be the magnitude of the gravitational potential at a point situated at a/2 distance from the centre ?
A−3GMRB−2GMRC−GMRD−4GMR
Following curve shows the variation of intesity of gravitational field (→I) with distance from the centre of solid sphere(r) :
View SolutionDependence of intensity of gravitational field (E) of earth with distance (r) from centre of earth is correctly represented by
View SolutionDependence of intensity of gravitational field (E) of earth with distance (r) from centre of earth is correctly represented by
View SolutionWhich graph correctley presents the variation of acceleration due to gravity with the distance form the centre of the earth?
View SolutionThe intensity of gravitational field at a point situated at a distance of 8000km form the centre of the earth is 6N/kg. The gravitational potential at that point is -(in joule /kg)
View SolutionBy which curve will be variation of gravitational potential of a hollow sphere of radius R with distance be depicted ?
View SolutionThe gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View Solution

