Which of the following is the graph between the height (h) of a projectile and time (t), when it is projected from the ground
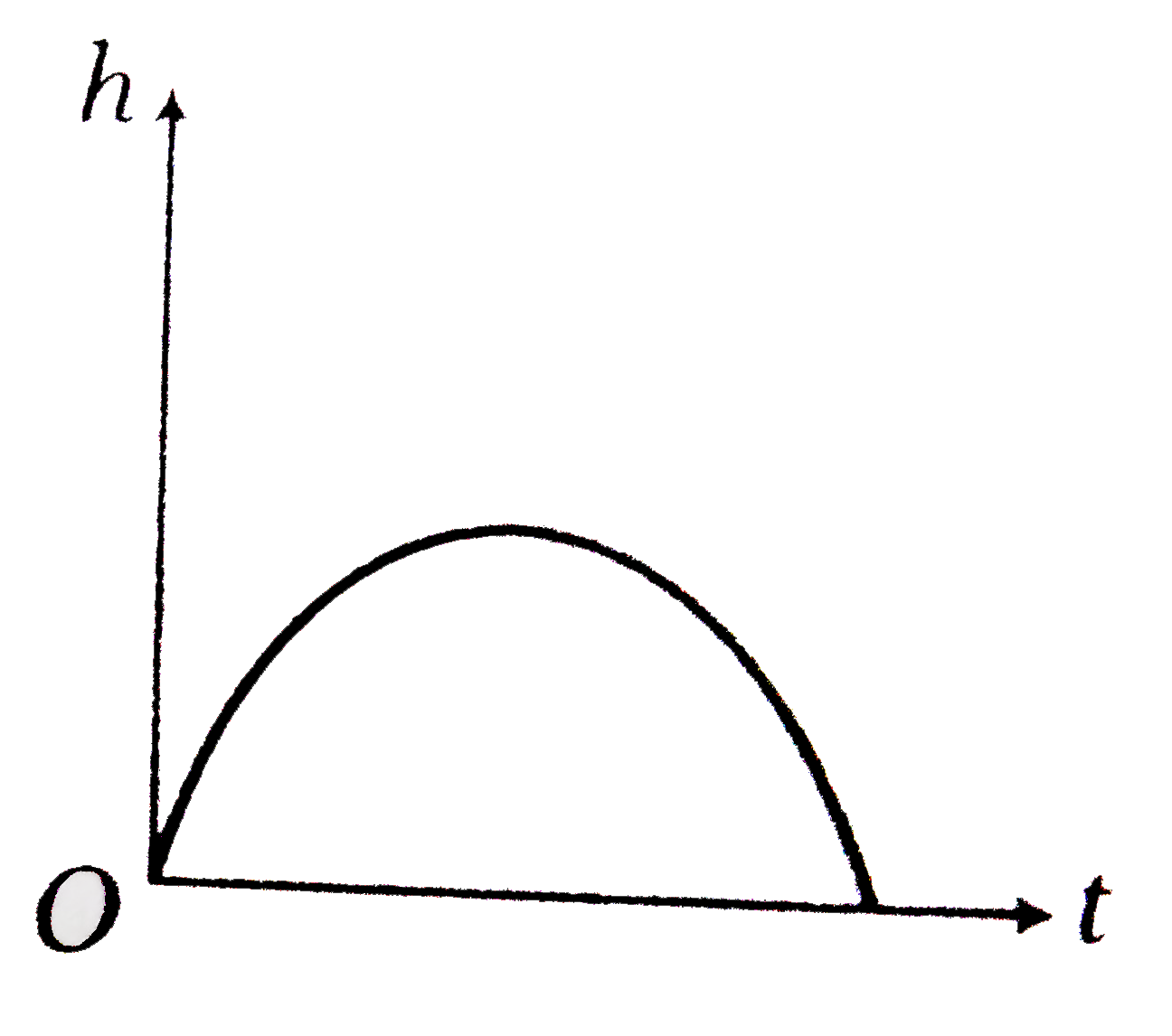
The correct Answer is:C
To determine the graph between the height (h) of a projectile and time (t) when it is projected from the ground, we can analyze the motion of the projectile step by step.
1. Understanding Projectile Motion:
- When a projectile is launched from the ground, it follows a parabolic trajectory. Initially, it rises to a maximum height and then falls back to the ground.
2. Initial Conditions:
- At time t=0, the height h=0 since the projectile is launched from the ground.
3. Equation of Motion:
- The height h of the projectile at any time t can be described by the equation:
h(t)=uyt−12gt2
- Where:
- uy=u0sin(α) is the initial vertical component of the velocity.
- g is the acceleration due to gravity (acting downwards).
4. Behavior of the Height with Time:
- As time increases from t=0, the height h increases until it reaches the maximum height.
- After reaching the maximum height, the height h starts to decrease until it returns to the ground (height h=0).
5. Graph Characteristics:
- The graph starts at the origin (0,0).
- It rises to a peak (maximum height) and then falls back to the horizontal axis (height = 0).
- This behavior indicates that the graph is a concave down parabola.
6. Analyzing Options:
- We need to identify which option represents this behavior:
- Option 1: Incorrect, as it does not start from (0,0).
- Option 2: Incorrect, as it does not decrease after reaching a maximum.
- Option 3: Correct, as it starts at (0,0), increases, and then decreases back to (0,0).
- Option 4: Incorrect, as it does not start from (0,0).
Conclusion:
The correct graph representing the height of a projectile as a function of time, when projected from the ground, is represented by Option 3.
- When a projectile is launched from the ground, it follows a parabolic trajectory. Initially, it rises to a maximum height and then falls back to the ground.
- At time t=0, the height h=0 since the projectile is launched from the ground.
- The height h of the projectile at any time t can be described by the equation:
h(t)=uyt−12gt2
- Where:
- uy=u0sin(α) is the initial vertical component of the velocity.
- g is the acceleration due to gravity (acting downwards).
- As time increases from t=0, the height h increases until it reaches the maximum height.
- After reaching the maximum height, the height h starts to decrease until it returns to the ground (height h=0).
- The graph starts at the origin (0,0).
- It rises to a peak (maximum height) and then falls back to the horizontal axis (height = 0).
- This behavior indicates that the graph is a concave down parabola.
- We need to identify which option represents this behavior:
- Option 1: Incorrect, as it does not start from (0,0).
- Option 2: Incorrect, as it does not decrease after reaching a maximum.
- Option 3: Correct, as it starts at (0,0), increases, and then decreases back to (0,0).
- Option 4: Incorrect, as it does not start from (0,0).
The correct graph representing the height of a projectile as a function of time, when projected from the ground, is represented by Option 3.
Topper's Solved these Questions
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:B. Medical entrance
Explore 1 Video
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:Medical entrance
Explore 12 Videos
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:A. Taking it together
Explore 1 Video
- MEASUREMENT AND ERRORSBook:DC PANDEY ENGLISHChapter:MEASUREMENT AND ERRORSExercise:Subjective
Explore 19 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:(C )Medical entrances gallery
Explore 32 Videos
Similar Questions
Knowledge Check
The relation between the time of flight of projectile Tf and the time to reach the maximum height tm is
ATf=2tmBTf=tmCTf=tm2DTf=√2(tm)The height of a boulder launched from a Roman catap can be described as a function of time according to the following quadratic equation: h(t)=−16t2+224t+240.
How much time elapese between the moment the boulder is launched and the moment it hits the ground, assuming that the ground is at a height of 0 ?A7B12C14D15
In a projectile motion, if we plot a graph between power of the force acting on the projectile and time, then it would be like
View SolutionThe horizontal range and the maximum height of a projectile are equal. The angle of projection of the projectile is
View SolutionA batsman hits a sixes and the ball touches the ground outside the cricket ground. Which of the following graph describes the variation of the cricket ball's vertical velocity v with time between the time t1 as it hits the bat and time t2 when it touches the ground?
View SolutionA ball falls from a height ‘h’ and collides with the ground. Each time it collides, its velocity is halved. Which of the following graphs are correct? Here t, v and y represent time, velocity and height above ground respectively. (vertically upwards direction is taken as positive and ground as y = 0)
View SolutionThere are two identical particles A and B. One is projected vertically upward with speed √2gh from ground and other is dropped from height h along the same vertical line. Collision between them is perfectly inelastic. Find time taken by them to reach the ground after collision in terms of √hg.
View SolutionA stone projected from ground with certain speed at an angle θ with horizontal attains maximum height h1 when it is projected with same speed at an angle θ with vertical attains height h2. The horizontal range of projectile is
View Solution

