A body of mass a moving with a velocity b strikes a body of mass c and gets embedded into it. The velocity of the systems after collision is
a+cab
aba+c
ab+c
aa+b
The correct Answer is:B
To solve the problem step by step, we will apply the principle of conservation of momentum.
Step 1: Identify the masses and their velocities
- Let the mass of the first body (A) be mA=A.
- The velocity of the first body (A) is uA=B.
- Let the mass of the second body (C) be mC=C.
- The initial velocity of the second body (C) is uC=0 (since it is at rest).
Step 2: Write the expression for initial momentum
The total initial momentum Pi of the system before the collision is given by:
Pi=mA⋅uA+mC⋅uC
Substituting the values:
Pi=A⋅B+C⋅0=A⋅B
Step 3: Write the expression for final momentum
After the collision, the two bodies get embedded into each other, and we can treat them as a single body with a combined mass:
mtotal=mA+mC=A+C
Let V be the common velocity of the combined mass after the collision. The final momentum Pf is then:
Pf=mtotal⋅V=(A+C)⋅V
Step 4: Apply the conservation of momentum
According to the conservation of momentum:
Pi=Pf
Substituting the expressions we derived:
A⋅B=(A+C)⋅V
Step 5: Solve for the final velocity V
Rearranging the equation to solve for V:
V=A⋅BA+C
Conclusion
Thus, the velocity of the system after the collision is:
V=A⋅BA+C
This matches with option 2 from the question.
---
- Let the mass of the first body (A) be mA=A.
- The velocity of the first body (A) is uA=B.
- Let the mass of the second body (C) be mC=C.
- The initial velocity of the second body (C) is uC=0 (since it is at rest).
The total initial momentum Pi of the system before the collision is given by:
Pi=mA⋅uA+mC⋅uC
Substituting the values:
Pi=A⋅B+C⋅0=A⋅B
After the collision, the two bodies get embedded into each other, and we can treat them as a single body with a combined mass:
mtotal=mA+mC=A+C
Let V be the common velocity of the combined mass after the collision. The final momentum Pf is then:
Pf=mtotal⋅V=(A+C)⋅V
According to the conservation of momentum:
Pi=Pf
Substituting the expressions we derived:
A⋅B=(A+C)⋅V
Rearranging the equation to solve for V:
V=A⋅BA+C
Thus, the velocity of the system after the collision is:
V=A⋅BA+C
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns
9 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA rod of mass m and length l hinged at the centre is placed on a horizontal surface. A bullet of mass m moving with velocity v strikes the end A of the rod and gets embedded in it. The angular velocity with which the systems rotates about its centre of mass after the bullet strikes the rod
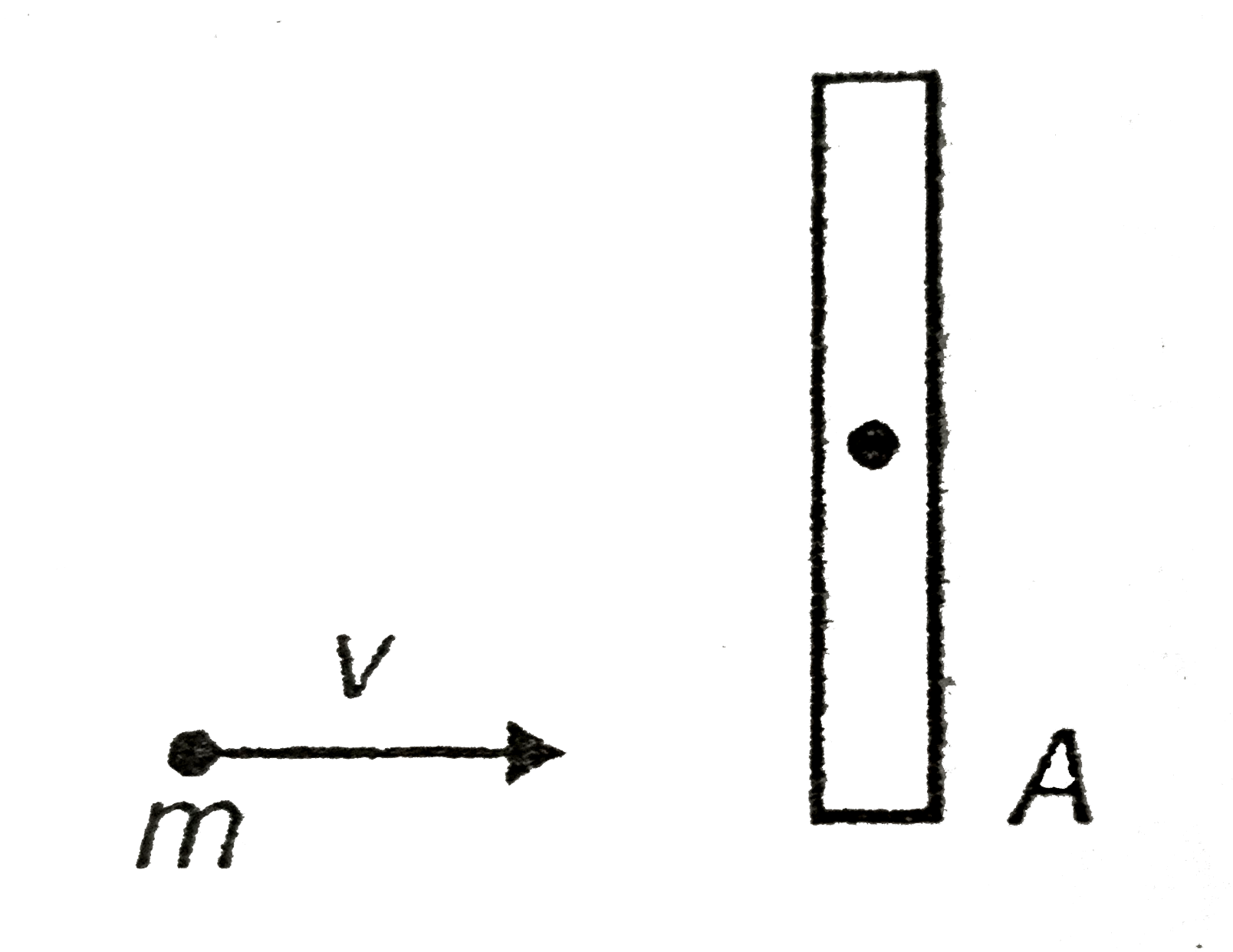
View Solution
Knowledge Check
A bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
Av22g(mM+m)2Bv22g(M+mm)2Cv22g(mM)2Dv22g(Mm)2
A circular wooden hoop of mass m and radius R rests fiat on a frictionless surface. A bullet, also of mass m and moving with a velocity v, strikes the hoop and gets embedded in it. The thickness of the hoop is much smaller than R. Find the angular velocity with which the system rotates in after the bullet strikes the hoop.
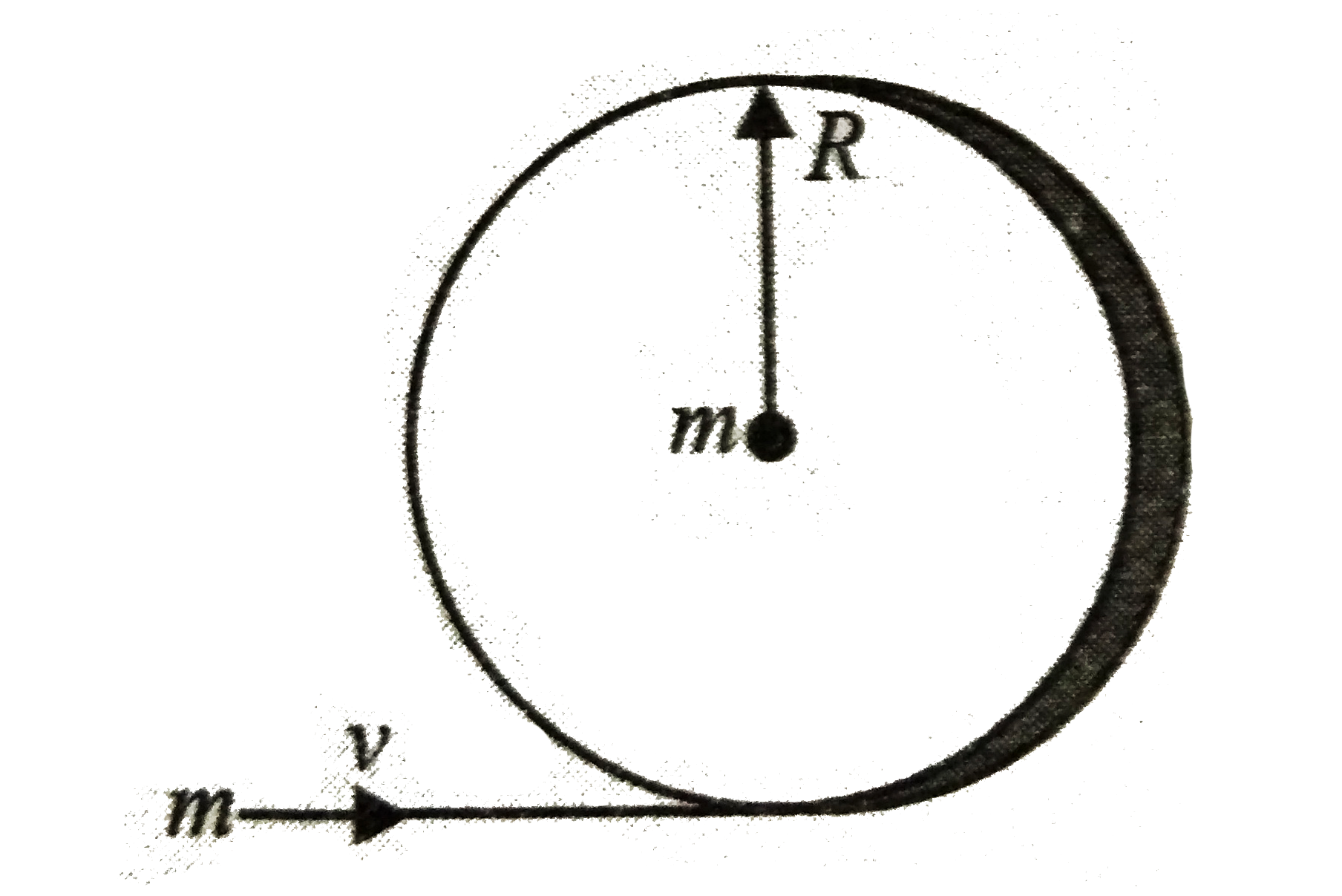
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionA body of mass m moving with a constant velocity v hits another body of the same mass moving with the same velocity v but in the opposite direction and sticks to it. The velocity of the compound body after collision is
View SolutionA body of mass 2kg moving with a velocity 3m/s collides with a body of mass 1kg moving with a velocity of 4m/s in opposite direction. If the collision is head on and completely inelastic, then
View SolutionA particle of mass m moving with velocity v strikes a stationary particle of mass 2m and sticks to it. The speed of the system will be.
A. v2
B. 2v
C. v3
D. 3v
View SolutionA body of mass 4kg moving with velocity 12m/s collides with another body of mass 6kg at rest. If two bodies stick together after collision , then the loss of kinetic energy of system is
View SolutionA body of mass 4kg moving with velocity 12m/s collides with another body of mass 6kg at rest. If two bodies stick together after collision , then the loss of kinetic energy of system is
View Solution
