The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of 4th dark fringe after a glass sheet of refractive index 1.5 is introduced. The thickness of glass sheet would be
4.8μm
4.2μm
5.4μm
3.0μm
The correct Answer is:B
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
Step 1: Understand the Shift of the Central Fringe
The central fringe shifts to the position of the 4th dark fringe when a glass sheet is introduced. The path difference for the dark fringes is given by the formula:
Path difference=(n+12)λ
where n is the order of the dark fringe. For the 4th dark fringe, n=3:
Path difference=(3+12)λ=72λ
Step 2: Calculate the Path Difference Due to the Glass Sheet
When a glass sheet of thickness T and refractive index μ is placed in front of one of the slits, it introduces an additional path difference. The path difference Δx introduced by the glass sheet is given by:
Δx=(μ−1)T
Here, the refractive index μ of the glass sheet is 1.5.
Step 3: Set Up the Equation
We know that the path difference created by the glass sheet must equal the path difference for the 4th dark fringe:
(μ−1)T=72λ
Substituting μ=1.5:
(1.5−1)T=72λ
This simplifies to:
0.5T=72λ
Step 4: Solve for Thickness T
Now, we can solve for T:
T=7λ0.5=14λ
Step 5: Substitute the Wavelength
The given wavelength λ is 6000 Å (angstroms). We need to convert this to meters for standard SI units:
λ=6000Å=6000×10−10m=6×10−7m
Now substituting this value into the equation for T:
T=14×(6×10−7m)=8.4×10−6m
Step 6: Convert to Micrometers
To express T in micrometers:
T=8.4×10−6m=8.4μm
Final Answer
Thus, the thickness of the glass sheet is:
8.4μm
The central fringe shifts to the position of the 4th dark fringe when a glass sheet is introduced. The path difference for the dark fringes is given by the formula:
Path difference=(n+12)λ
where n is the order of the dark fringe. For the 4th dark fringe, n=3:
Path difference=(3+12)λ=72λ
When a glass sheet of thickness T and refractive index μ is placed in front of one of the slits, it introduces an additional path difference. The path difference Δx introduced by the glass sheet is given by:
Δx=(μ−1)T
Here, the refractive index μ of the glass sheet is 1.5.
We know that the path difference created by the glass sheet must equal the path difference for the 4th dark fringe:
(μ−1)T=72λ
Substituting μ=1.5:
(1.5−1)T=72λ
This simplifies to:
0.5T=72λ
Now, we can solve for T:
T=7λ0.5=14λ
The given wavelength λ is 6000 Å (angstroms). We need to convert this to meters for standard SI units:
λ=6000Å=6000×10−10m=6×10−7m
Now substituting this value into the equation for T:
T=14×(6×10−7m)=8.4×10−6m
To express T in micrometers:
T=8.4×10−6m=8.4μm
Thus, the thickness of the glass sheet is:
8.4μm
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:LEVEL 2 (single correct option)
Explore 1 Video
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:Level 2 More Than One Correct
Explore 6 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:Subjective Questions
Explore 5 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:All Questions
Explore 135 Videos
- MAGNETIC FIELD AND FORCESBook:DC PANDEY ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
Similar Questions
To make the central fringe at the centerO , mica sheet of refractive index 1.5 is introduced Choose the corect statement.
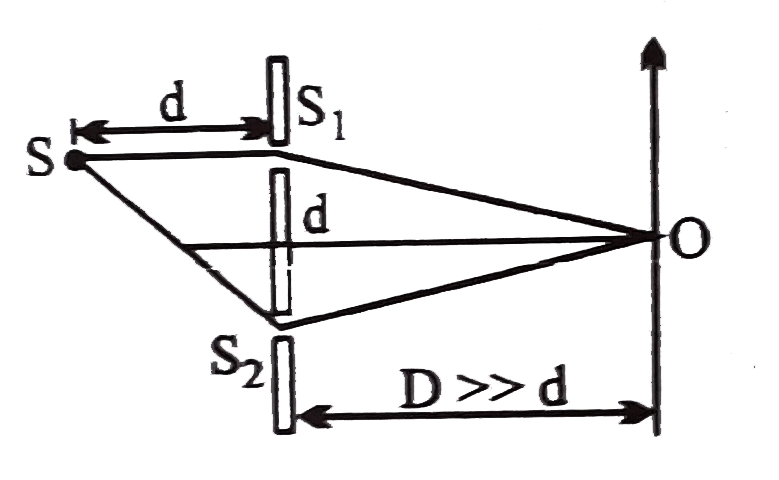
View SolutionA ray of light 10−9 second to cross a glass slab of refractive index 1.5. The thickness of the slab will be
View SolutionThe central fringe shifts to the position of fifth bright fringe, if a thin film of refractive index 1.5 is introduced in the path of light of wavelength 5000Å. The thickness of the glass plate is
View SolutionA young's double slit apporatus is immersed in a liquid of refractive index 1.33.It has slit separation of 1 mm and interference pattern is observed on the screen at a distance 1.33 m from plane of slits.The wavelength in air is 6300Å
One of the slits of the apparatus is covered by a thin glass sheet of refractive index 1.53. Find the smallest thickness of the sheet to interchange the position of minima and maxima .
View SolutionTo make the central fringe at the center O , a mica - sheet index 1.5 is introduced .Choose the correct statement (s)
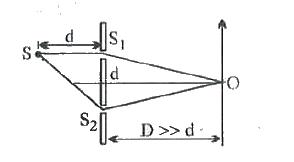
View SolutionA young's double slit apporatus is immersed in a liquid of refractive index 1.33.It has slit separation of 1 mm and interference pattern is observed on the screen at a distance 1.33 m from plane of slits.The wavelength in air is 6300Å
One of the slits of the apparatus is covered by a thin glass sheet of refractive index 1.53. Find the fringe width
View SolutionLight of wavelength 4500Å in vacuum enters into a glass block of refractive index 1.5. What is the wavelength of light in the glass block?
View SolutionA double - slit apparatus is immersed in a liquid of refractive index 1.33 it has slit separation of 1mm and distance between the plane of slits and screen 1.33 m the slits are illuminated by a parallel beam of light whose wavelength in air is 800 nm.
(i) Calculate the fringe width.
(ii) One of the slits of apparatus is covered by a thin glass sheet of refractive index 1.53 Find the smallest thickness of the sheet to bring the adjacent minima on the axis.
View SolutionLight of wavelength 6000A is incident on a thin glass plate of refractive index 0.5 such that angle of refraction into plate is 60° .calculate the thickness of plate which will make it appear dark by reflection?
View SolutionLight of wavelength 3000A is incident on a thin glass plate of refractive index 1.5 such that angle of refraction into plate is 60° .calculate the thickness of plate which will make it appear dark by reflection?
View Solution