figure shows three equidistant slits illuminated by a monochromatic parallel beam of light. Let and .
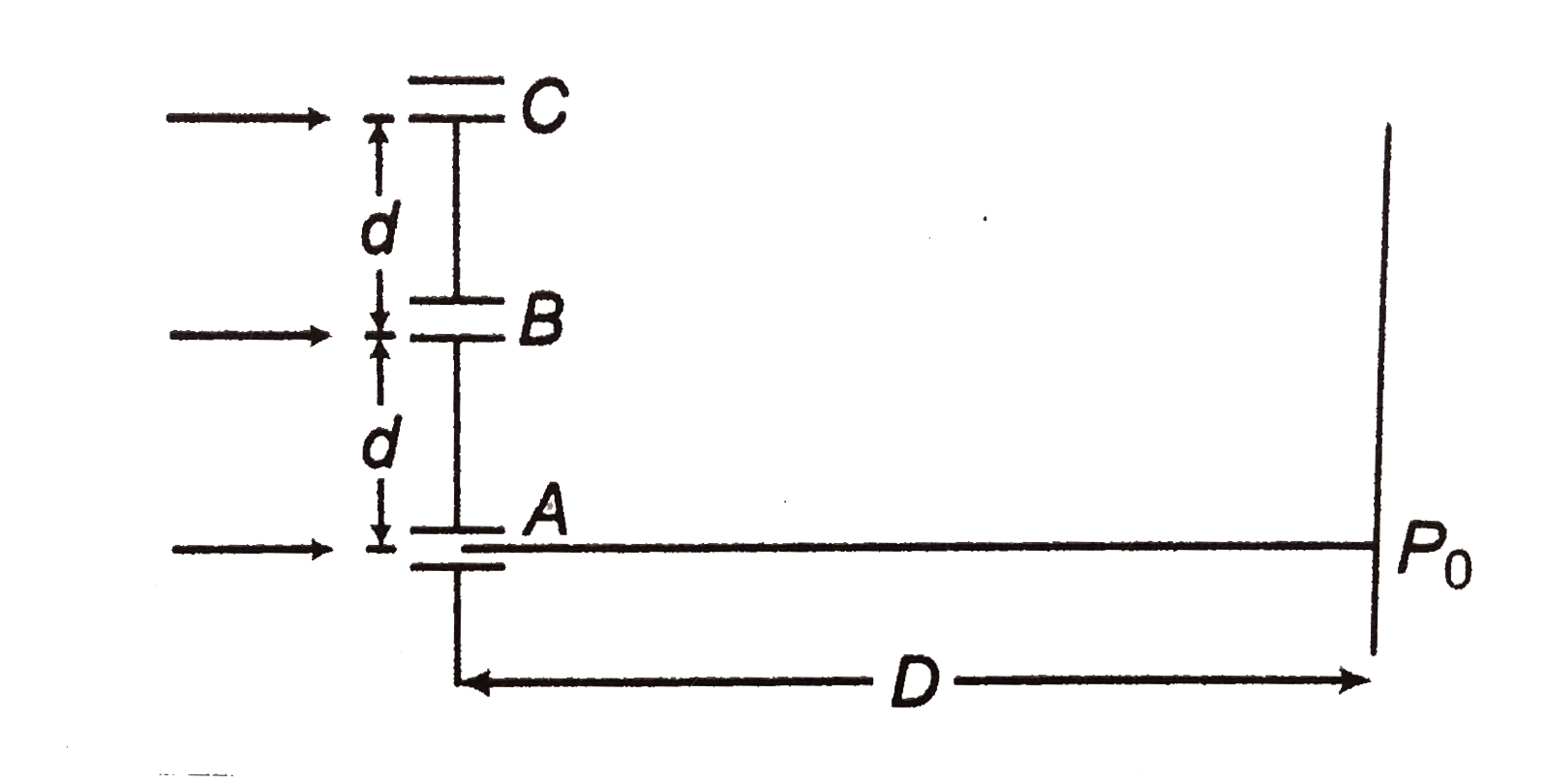
(a) Show that d =
(b) Show that the intensity at is three times the intensity due to any of the three slits
individually.
The correct Answer is:A, B
(a) Given,
sqrt(D^2 + d^2) -D = lambda/3 sqrt (D^2+d^2) = (D+ (lambda/3)) D^2 + d^2 = D^2 + lambda^2/9 + (2Dlambda)/3lambdaltltDlambda_2/9d= sqrt(2lambdaD)/3BP_0 - AP_0 = Deltax_(12) = lambda/3:. Delta phi_(12)phi_(12) = 120^@ CP_0 - AP_0 = Deltax_(13) = sqrt(2d)^2 + d^2)- D = D[1+((2d)/D)^2]^(1/2)- D= D[ 1+ 1/2 xx (4d^2)/D^2] - D= (2d^2)/Dd=sqrt(2lambdaD)/3d^2 = (2lambdaD)/3Deltax_(13) = 4/3 lambda:. Delta phi(13)phi(13) = 4/3(360^@) = 480^@ = 480^@ - 360^@ = 120^@A_0 A = sqrt (A_(0)^2 + (2A_0)^2 + 2(A_0)(2A_0)cos 120^@)sqrt 3 A_0I prop A^2sqrt3 times, therefore resultant intensity will become 3 times.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:Exercise 32.1
Explore 3 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:Exercise 32.2
Explore 6 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:Example Type 6
Explore 3 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:All Questions
Explore 135 Videos
- MAGNETIC FIELD AND FORCESBook:DC PANDEY ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
Similar Questions
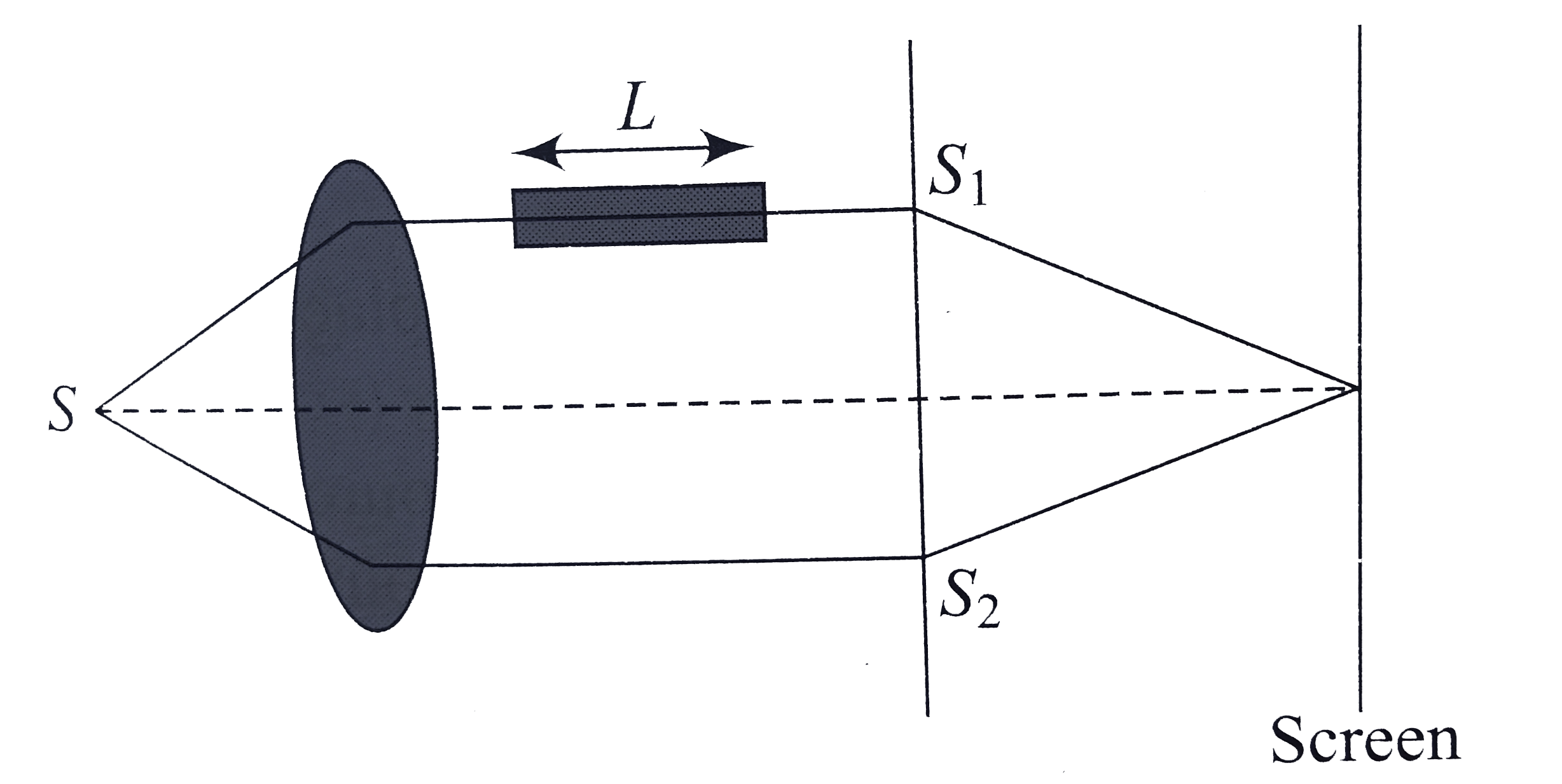
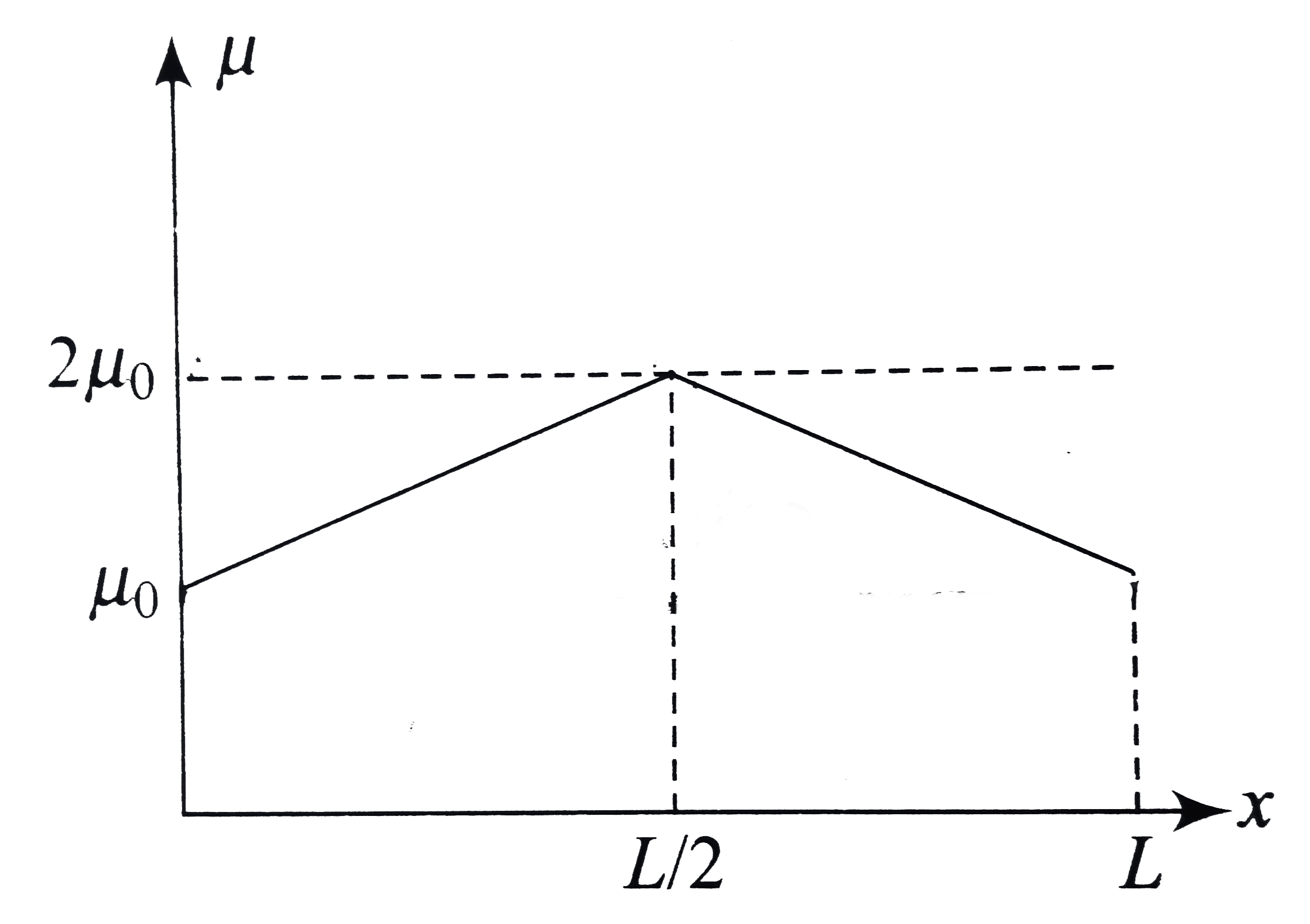
Figure shows a narrow slit S illuminated b a monochromatic light of wavelength λ in a double-slit experiment. In the path of the rays reaching the upper slit S1, a tube to length L is interposed in which the index of reflection of the medium varies linearly as shown in figure . The position of the central maximum in the interference pattern on the screen was displaceed by N fringes. Find the value of N in terms of μ0, L and λ.
View Solution_E01_054_Q01.png)
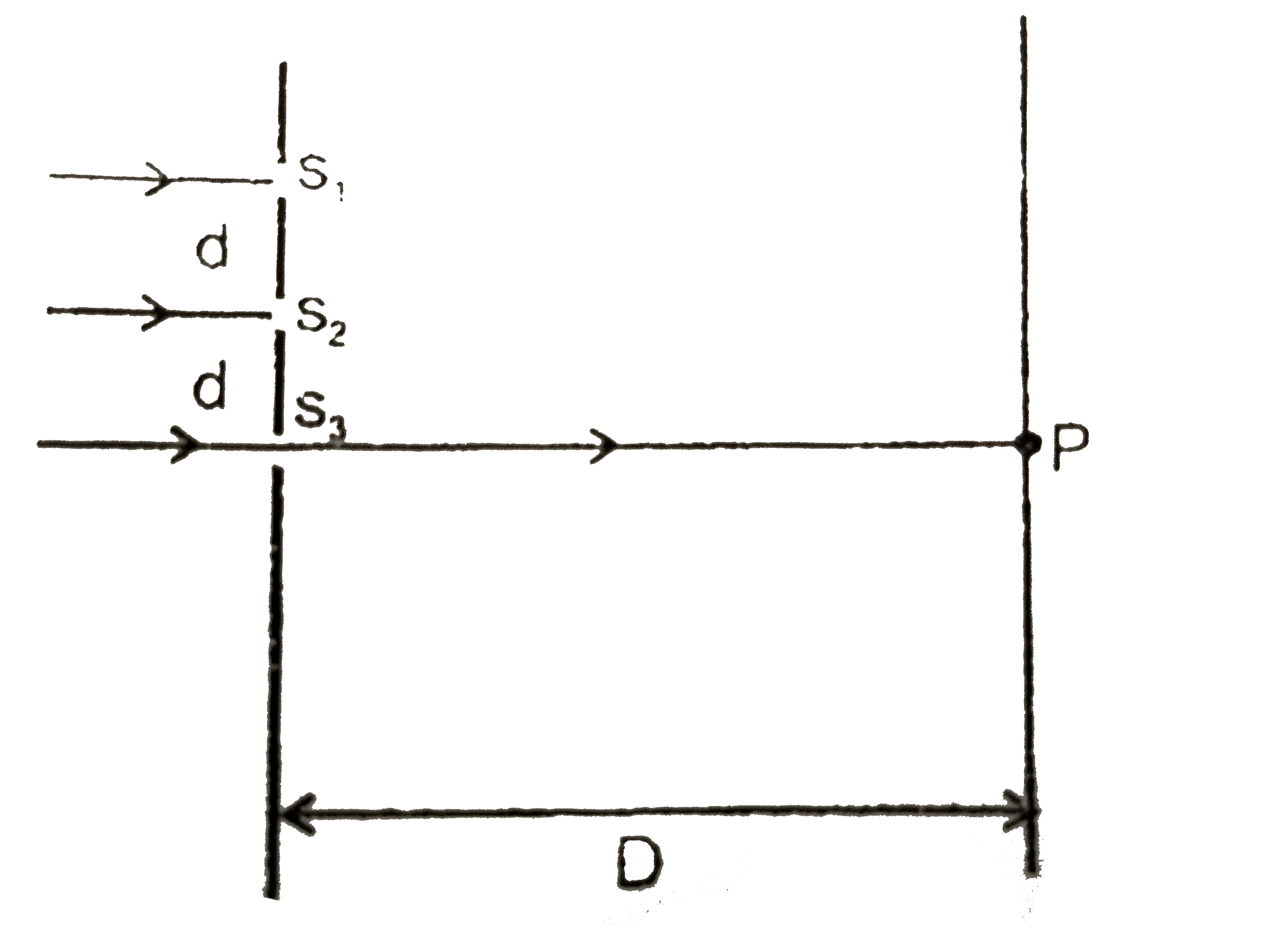
A monochromatic light source of wavelength λ is placed at S. three slits S1,S2 and S3 are equidistant from the source S and the point P on the screen S1P−S2P=λ/6 and S1P−S3P=2λ/3. if I be the intensity at P when only one slit is open the intensity at P when all the three slits are open is-
View SolutionA Young's double slit experiment uses a monochromatic light of wavelength λ. The intensity of each slit is same and is equal to I0. What will be the resultant intensity at a point where waves interfere at a path difference of λ2 ?
View SolutionIn the figure shown three slits s1,s2 and s3 are illuminated with of wavelength λ.λ<<d and D>>d. Each slit prouduces same intensity I on the screen. If intensity at the point on screen directly infront of s2 is 3I then the maximum value of λ is nd22D Find value of n.
View SolutionIn a Young's double slit set up using monochromatic light of wavelength λ the intensity of light at a point, where path difference is 2λ is found to be I0 What will be the intensity at a point when path different is λ/3 ?
View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

View SolutionConsider the situation shown in figure. The two slite S1andS2
placed symmetrically around the centre line are illuminated by a monochromatic
light of wavelength lambda. The separation between the slits is d. The light transmitted
by the slits falls on a screen M1 placed at a distance D from the slits. The slit S3 is
at the centre line and the slit S4 is at a distance y form S3. Another screen M2 is
placed at a further distance D away from M1. Find the ration of the maximum to
minimum intensity observed on M2 if y is equal to (d<<D).
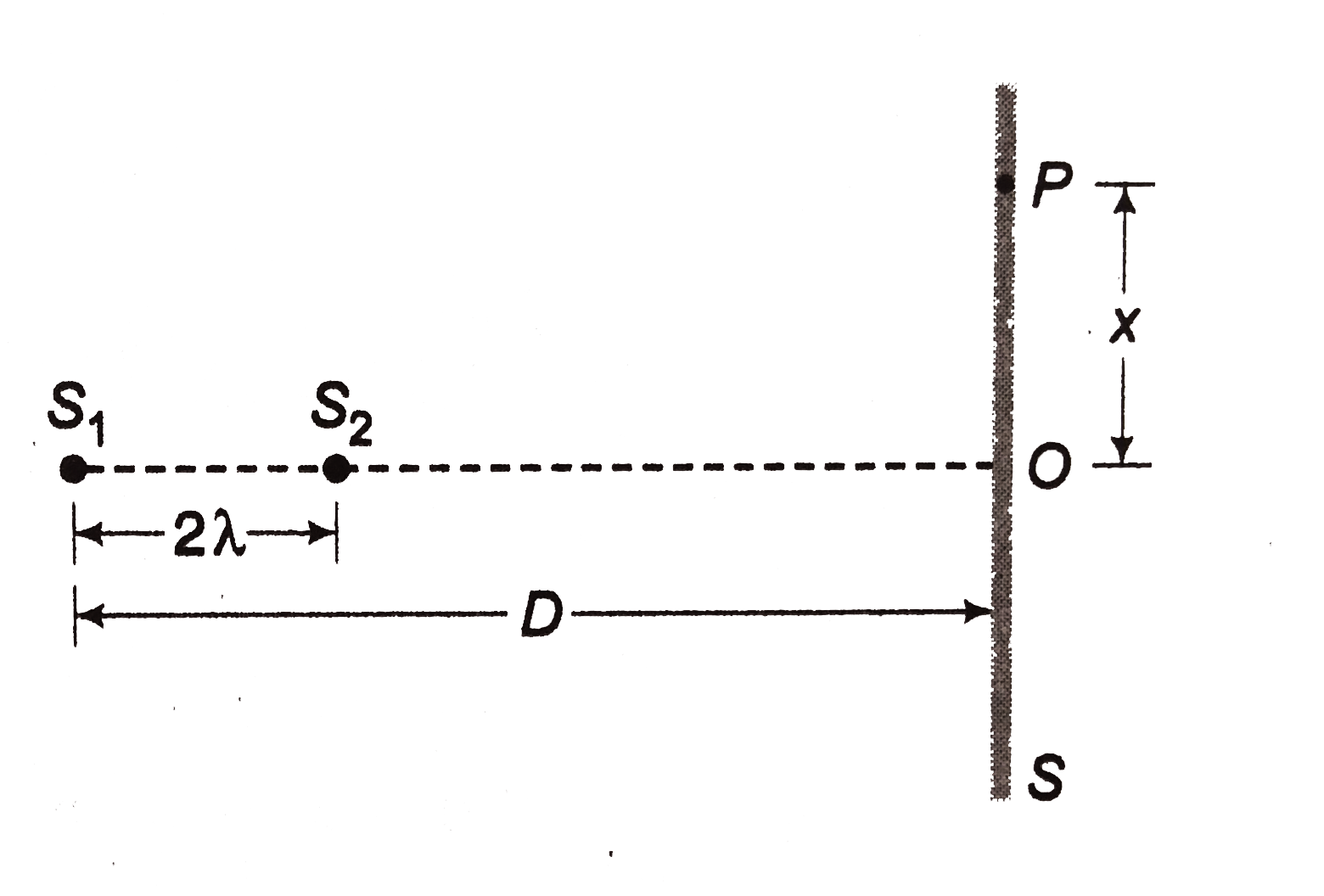
View SolutionTwo coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(gtgtλ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O.
 .
.
View SolutionShow that the three straight lines 2x−3y+5=0,3x+4y−7=0and9x−5y+8=0 meet in a point
View SolutionShow that the points A(2,1),B(0,3),C(−2,1)andD(0,−1) are the vertices of a square.
View Solution