The refracting angle of a prism is A and refractive index of the material of prism is cot(A/2) . The angle of minimum deviation will be
180∘−3A
180∘+2A
90∘−A
180∘−2A
The correct Answer is:B
To solve the problem, we need to find the angle of minimum deviation (Δ_min) for a prism with a refracting angle (A) and a refractive index (μ) given by cot(A/2).
1. Understanding the Given Information:
- Refracting angle of the prism: A
- Refractive index of the prism material: μ = cot(A/2)
2. Using the Formula for Refractive Index:
- The refractive index (μ) for a prism in terms of the angle of minimum deviation (Δ_min) is given by:
μ=sin(A+Δmin2)sin(A2)
3. Substituting the Given Refractive Index:
- We substitute μ = cot(A/2) into the formula:
cot(A2)=sin(A+Δmin2)sin(A2)
4. Expressing Cotangent in Terms of Sine and Cosine:
- Recall that cot(x) = cos(x)/sin(x):
cos(A2)sin(A2)=sin(A+Δmin2)sin(A2)
5. Cross Multiplying:
- Cross-multiplying gives:
cos(A2)⋅sin(A2)=sin(A+Δmin2)
6. Using the Identity for Sine:
- We can express cos(A/2) as sin(90° - A/2):
sin(90∘−A2)=sin(A+Δmin2)
7. Setting Up the Equation:
- From the sine identity, we have:
90∘−A2=A+Δmin2
8. Solving for Δ_min:
- Rearranging gives:
180∘−A=A+Δmin
- Therefore:
Δmin=180∘−2A
9. Final Answer:
- The angle of minimum deviation is:
Δmin=180∘−2A
- Refracting angle of the prism: A
- Refractive index of the prism material: μ = cot(A/2)
- The refractive index (μ) for a prism in terms of the angle of minimum deviation (Δ_min) is given by:
μ=sin(A+Δmin2)sin(A2)
- We substitute μ = cot(A/2) into the formula:
cot(A2)=sin(A+Δmin2)sin(A2)
- Recall that cot(x) = cos(x)/sin(x):
cos(A2)sin(A2)=sin(A+Δmin2)sin(A2)
- Cross-multiplying gives:
cos(A2)⋅sin(A2)=sin(A+Δmin2)
- We can express cos(A/2) as sin(90° - A/2):
sin(90∘−A2)=sin(A+Δmin2)
- From the sine identity, we have:
90∘−A2=A+Δmin2
- Rearranging gives:
180∘−A=A+Δmin
- Therefore:
Δmin=180∘−2A
- The angle of minimum deviation is:
Δmin=180∘−2A
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Objective Questions1videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Subjective29videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Assertion And Reason13videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
The refracting angle of a prism is A, and refractive index of the material of the prism is cot(A2). The angle of minimum deviation is
View SolutionThe refractive index of the material of prism √3, then the angle of minimum deviation of prism is
View SolutionThe refracting angle of the prism is 60∘ and the refractive index of the material of the prism is √3. Calculate the angle of minimum deviation in degree.
View SolutionA ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A=60∘ and the refractive index of the material of prism is 3^1/2, then the angle of deviation of the ray is
 View Solution
View SolutionWhen light rays are incident on a prism at an angle of 45∘, the minimum deviation is obtained. If refractive index of the material of prism is √2, then the angle of prism will be
View SolutionThe correct relation between the refractive index (μ) of the material of prism (A) and angle of minimum deviation (δ) is
View SolutionA certain prism of refracting angle 60∘ and of refractive index 2 is immersed in a liquid of refractive index √2 then the angle of minimum deviation will be
View SolutionIn an isosceles prism of angle 45∘, it is found that when the angle of incidence is same as the prism angle, the emergen ray grazes the emergent surface.
Find the refractive index of the material of the prism. For what angle of incidenc, the angle of deviation will be minimum?
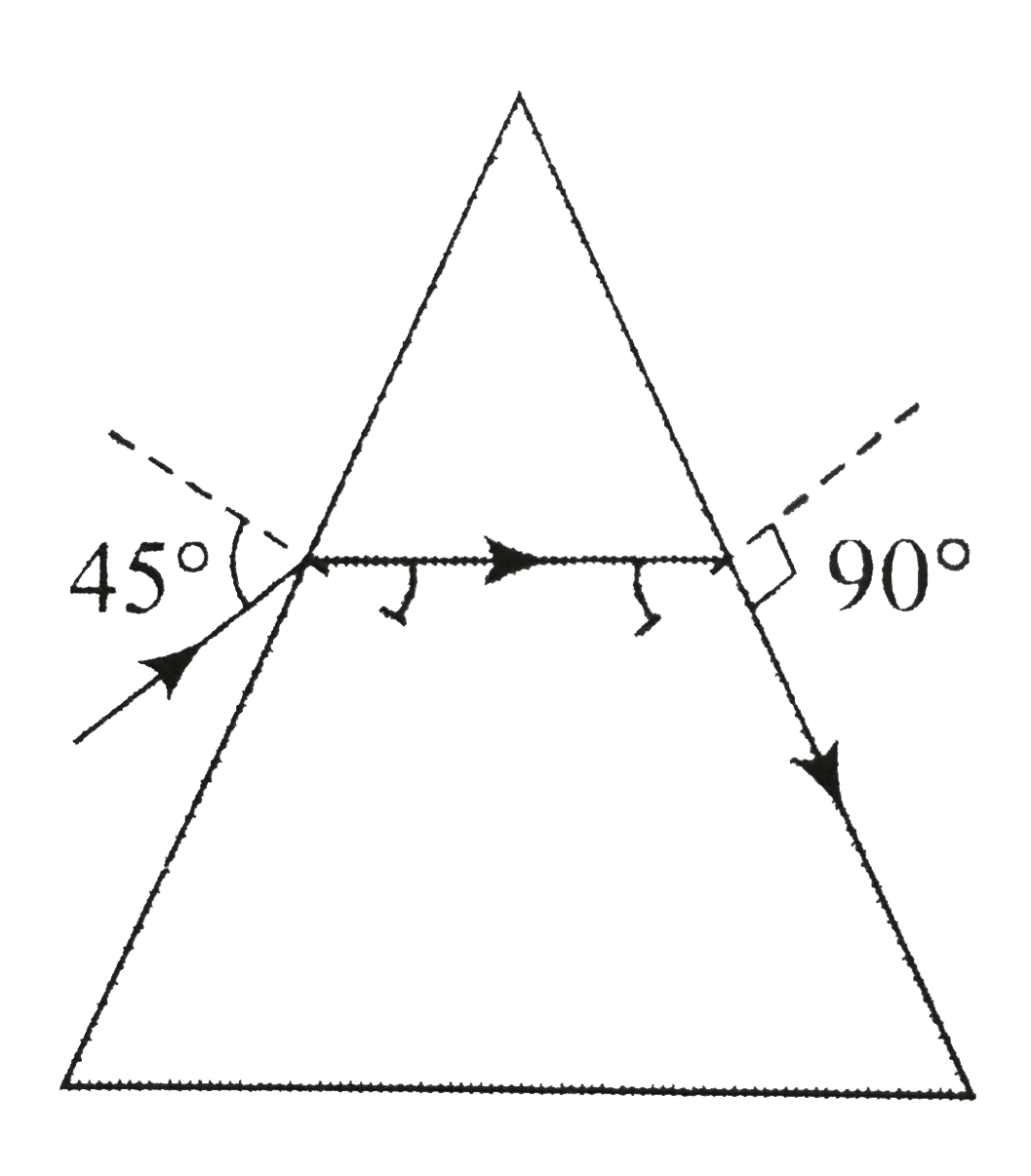 View Solution
View SolutionA prism is made up of material of refractive index √3. The angle of prism is A. If the angle of minimum deviation is equal to the angle of the prism, then the value of A is
View Solution(a) Plot a graph for angle of deviation as a function of angle of incidence for a triangular prism.
(b) Derive the relation for the refractive index of the prism in terms of the angle of minimum deviation and angle of prism.View Solution
