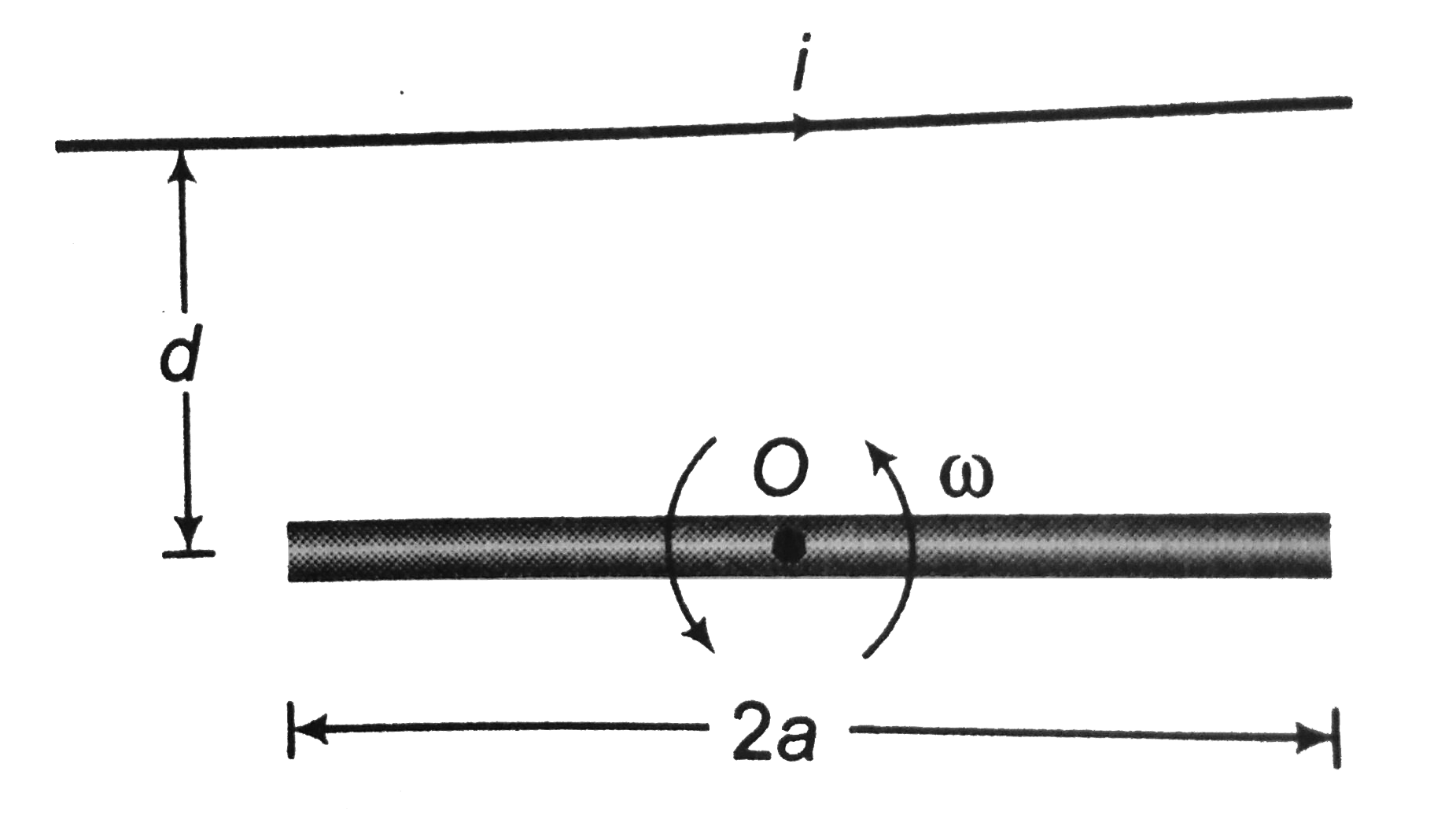
A rod of length 2a is free to rotate in a vertical plane, about a horizontal axis O passing through its mid-point. A long straight, horizontal wire is in the same plane and is carrying a constant current i as shown in figure. At initial moment of time, the rod is horizontal and starts to rotate with constant angular velocity ω, calculate emf induced in the rod as a function of time.
The correct Answer is:A, B
θ=ωt
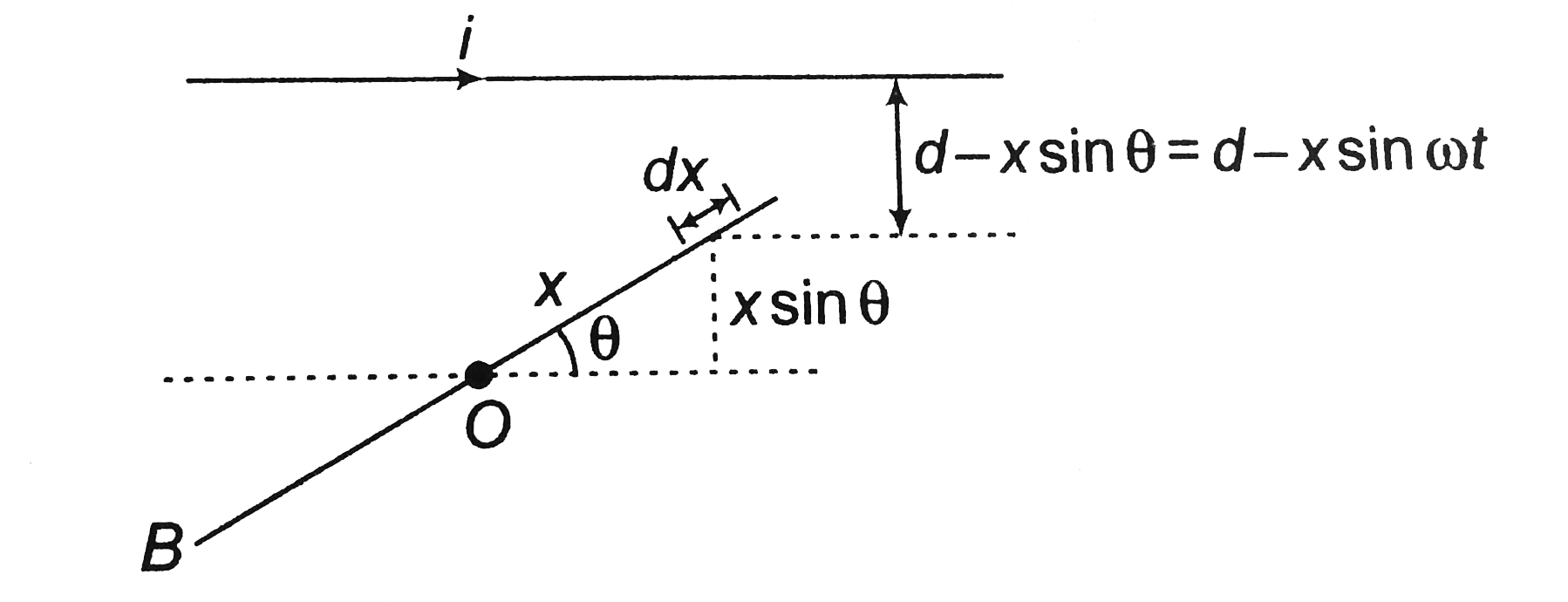
de=B(ωx)dx
Here B=μ02πid−xsinωt
∴de=μ0iω2πxd−xsinωtdx
VOA=V0−VA=∫a0de=μoiω2π∫a0xd−xsinωtdx
=−μ0iω2πsinωt[dsinωtIn(d−asinωtd)+a]
Similarly,
VOB=VO−VB=μ0iω2π∫a0xd+xsinωtdx
=μ0iω2πsinωt[a−dsinωtIn(d+asinωtd)]
∴VAB=VOB−VOA
=μ0iω2πsinωt[2a+dsinωtIn(d−asinωtd+asinωt)]
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example
71 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - SUBJECTIVE TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View Solution
A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

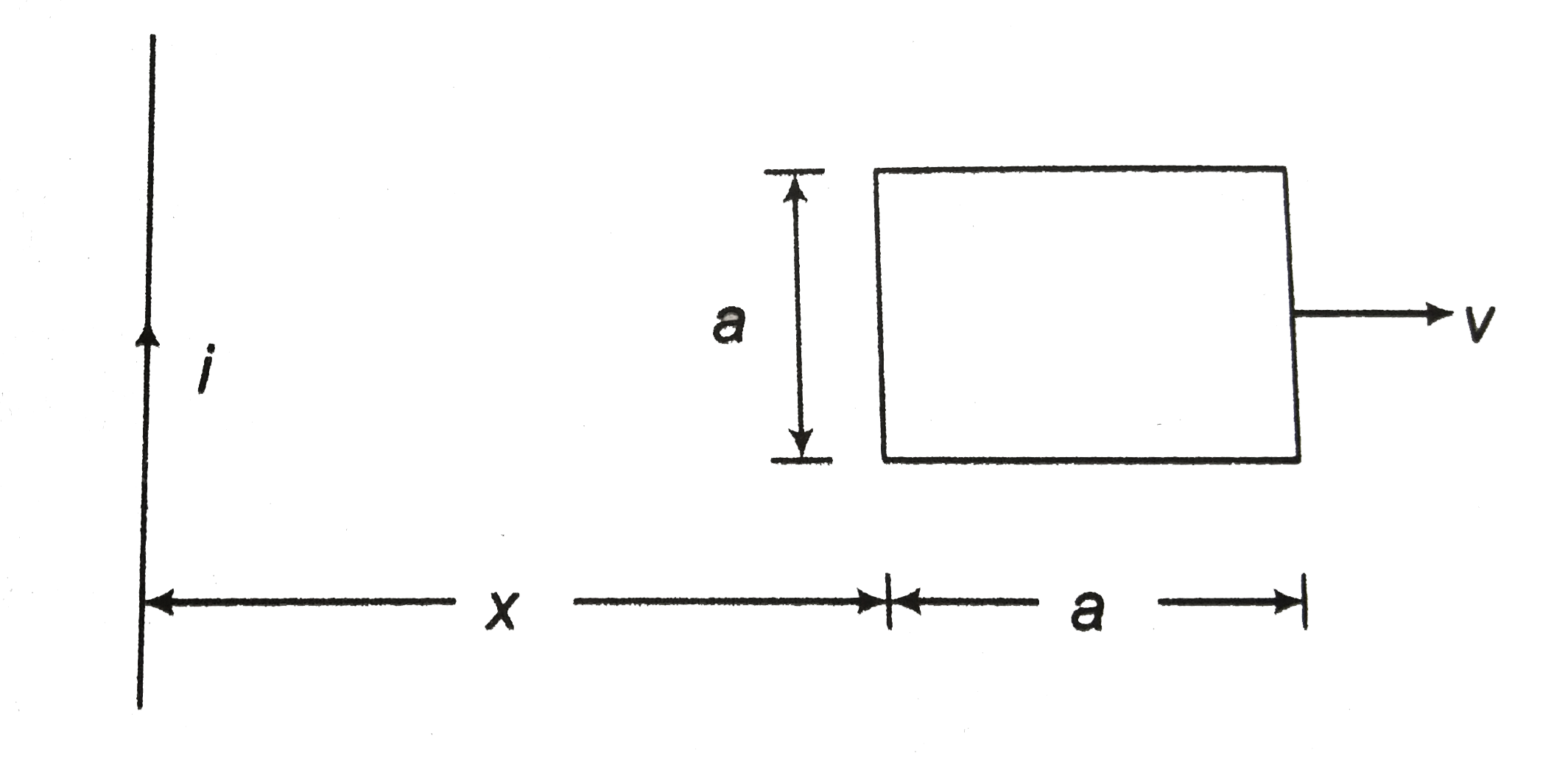
View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
View SolutionAB is a mass less rigid rod of length 2l. It is free to rotate in vertical plane about a horizontal axis passing through its end A. Equal point masses (m each) are stuck at the centre C and end Bof the rod. The rod is released from horizontal position. Write the tension in the rod when it becomes vertical.

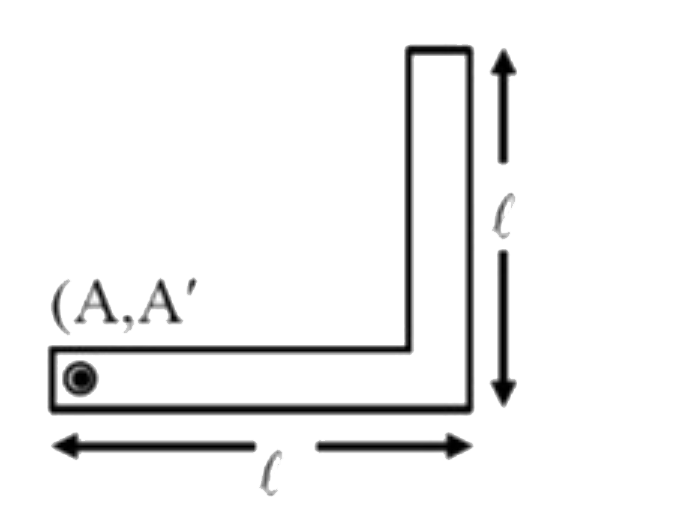
View SolutionA L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is
View SolutionA uniform rod of length L is free to rotate about an axis passing through O. Inititally the rod is horizontal. The rod is relased from this position. Match column I with column II
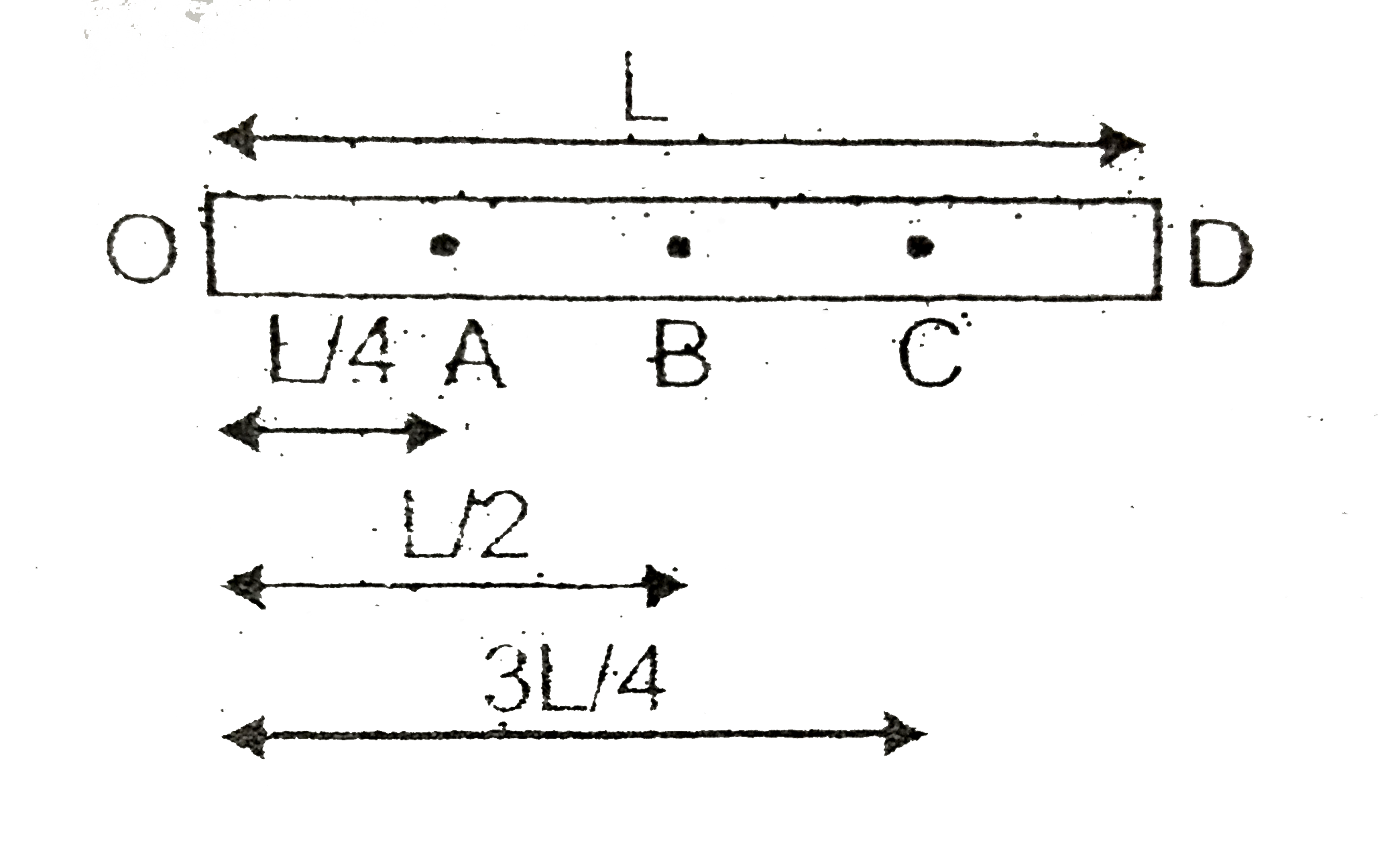
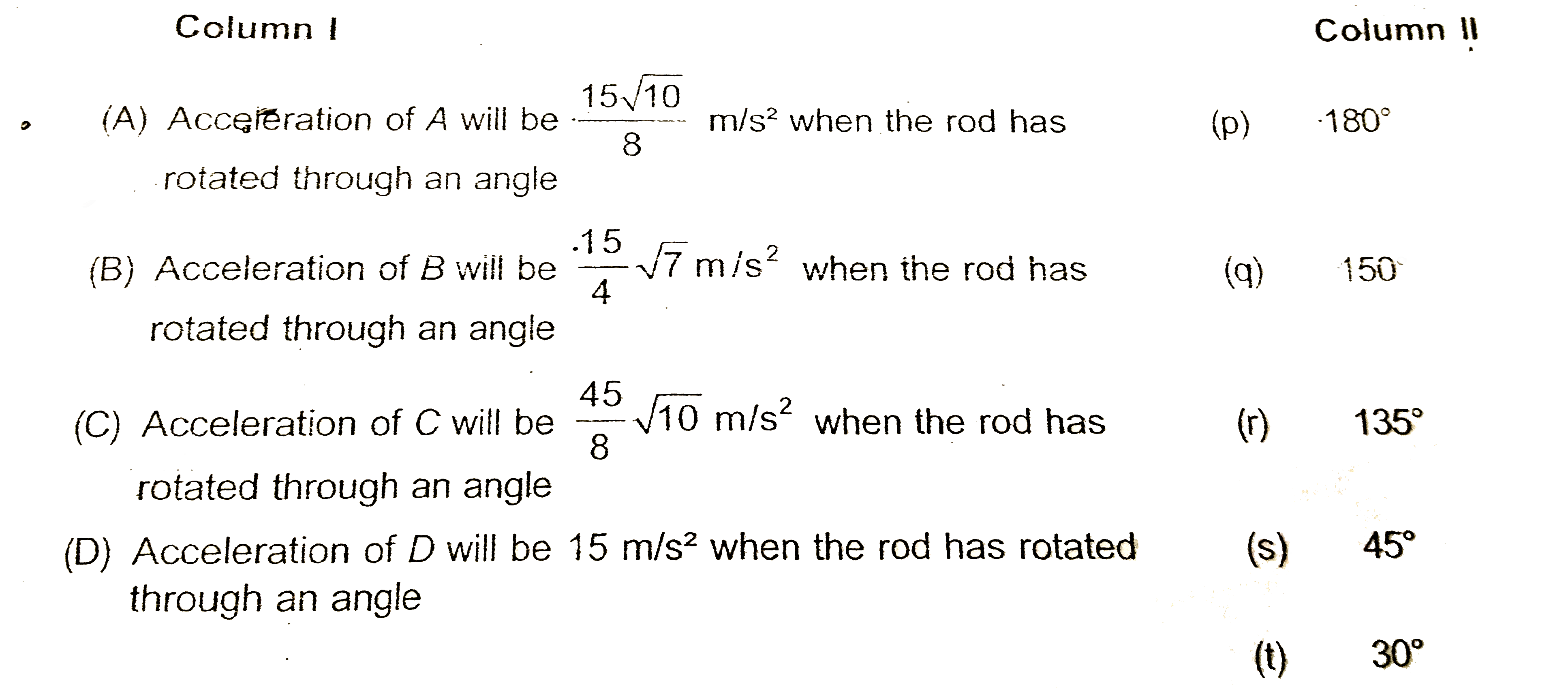
View SolutionA thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin]

View SolutionAn L shaped thin uniform rod of total length 2l is free to rotate in a vertical plane about a horizontal axis a P as shown in the figure. The bas is released from rest. Neglect air and contact friction. The angular velociyt at the instant it has rotated through 90∘ and reached the dotted position shown is
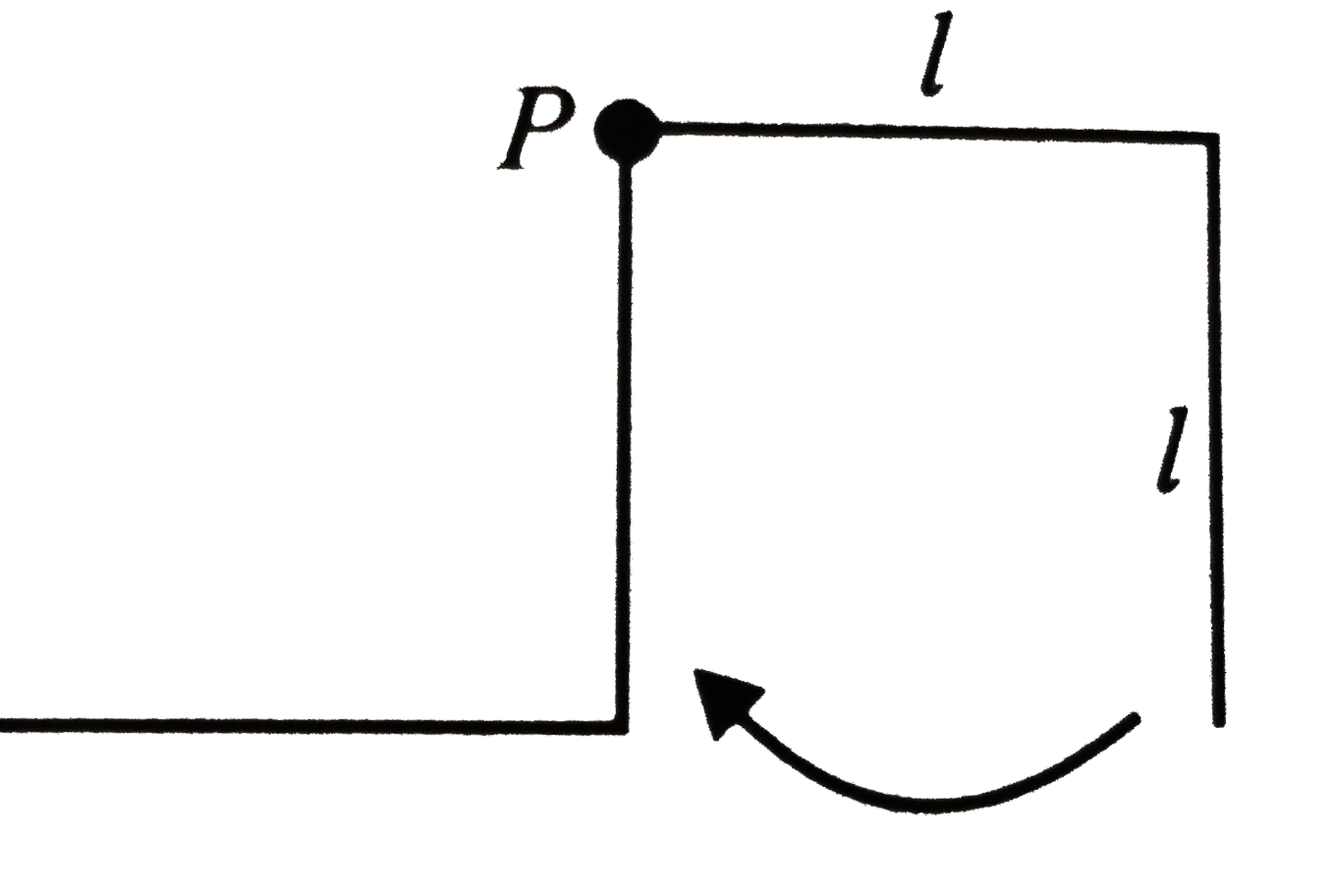
View Solution
