A 5H inductor is placed in series with a 10Ω resistor. An emf of 5V being suddenly applied to the combination. Using these values prove the principle of conservation of energy, for time equal to the time constant.
To solve the problem, we will follow these steps:
Step 1: Identify the given values
- Inductance (L) = 5 H
- Resistance (R) = 10 Ω
- EMF (E) = 5 V
Step 2: Calculate the time constant (τ)
The time constant (τ) for an LR circuit is given by the formula:
τ=LR
Substituting the given values:
τ=5H10Ω=0.5s
Step 3: Calculate the maximum current (I₀)
The maximum current (I₀) in the circuit can be calculated using Ohm's law:
I0=ER
Substituting the values:
I0=5V10Ω=0.5A
Step 4: Calculate the current (I) at time t = τ
The current (I) at any time t in an LR circuit is given by:
I(t)=I0(1−e−tτ)
At t=τ:
I(τ)=I0(1−e−1)
Substituting the value of I0:
I(τ)=0.5(1−1e)≈0.5(1−0.3679)≈0.5×0.6321≈0.316A
Step 5: Calculate the power delivered by the battery (P₁)
The power delivered by the battery is given by:
P1=E⋅I
Substituting the values:
P1=5V×0.316A≈1.58W
Step 6: Calculate the power dissipated by the resistor (P₂)
The power dissipated in the resistor can be calculated using:
P2=I2⋅R
Substituting the values:
P2=(0.316A)2×10Ω≈0.998W
Step 7: Calculate the energy stored in the inductor (P₃)
The energy stored in the inductor can be calculated using:
P3=E⋅Ie
Substituting the values:
P3=5V×0.316A2.718≈0.582W
Step 8: Verify the conservation of energy
According to the principle of conservation of energy:
P1=P2+P3
Substituting the calculated values:
1.58W=0.998W+0.582W
This holds true, thus proving the principle of conservation of energy.
- Inductance (L) = 5 H
- Resistance (R) = 10 Ω
- EMF (E) = 5 V
The time constant (τ) for an LR circuit is given by the formula:
τ=LR
Substituting the given values:
τ=5H10Ω=0.5s
The maximum current (I₀) in the circuit can be calculated using Ohm's law:
I0=ER
Substituting the values:
I0=5V10Ω=0.5A
The current (I) at any time t in an LR circuit is given by:
I(t)=I0(1−e−tτ)
At t=τ:
I(τ)=I0(1−e−1)
Substituting the value of I0:
I(τ)=0.5(1−1e)≈0.5(1−0.3679)≈0.5×0.6321≈0.316A
The power delivered by the battery is given by:
P1=E⋅I
Substituting the values:
P1=5V×0.316A≈1.58W
The power dissipated in the resistor can be calculated using:
P2=I2⋅R
Substituting the values:
P2=(0.316A)2×10Ω≈0.998W
The energy stored in the inductor can be calculated using:
P3=E⋅Ie
Substituting the values:
P3=5V×0.316A2.718≈0.582W
According to the principle of conservation of energy:
P1=P2+P3
Substituting the calculated values:
1.58W=0.998W+0.582W
This holds true, thus proving the principle of conservation of energy.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Subjective
20 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A 3.56H inductor is placed in series with a 12.8Ω resistor. An emf of 3.24V is then suddenly applied across the RL combination.
(a) At 0.278s after the emf is applied what is the rate at which energy is being delivered by the battery?
(b) At 0.278s, at what rate is energy appearing as thermal energy in the resistor? (c) At0.278s, at what rate is energy being stored in the magnetic field?
View SolutionA 20 H inductor is placed in series with 10 W resistor and an emf of 100 V is suddenly applied to the combination. At t = 1 s from t = 1 s from the start, find the rate at which energy is being stored in the magnetic field around the inductor (givne e−0.5=0.61).
View SolutionA coil of 40H inductance is connected in series with a resistance of 8 ohm and the combination is joined to the terminals of a 2V battery. The time constant of the circuit
View SolutionAn emf of 15V is applied in a circuit containing 5H inductance and 10Ω resistance. The ratio of the currents at time t=∞ and t=1s is
View SolutionA 20 Henry inductor coil is connected to a 10ohm resistance in series as shown in figure. The time at which rate of dissipation of energy (Joule's heat) across resistance is equal to the rate at which magnetic energy is stored in the inductor, is:
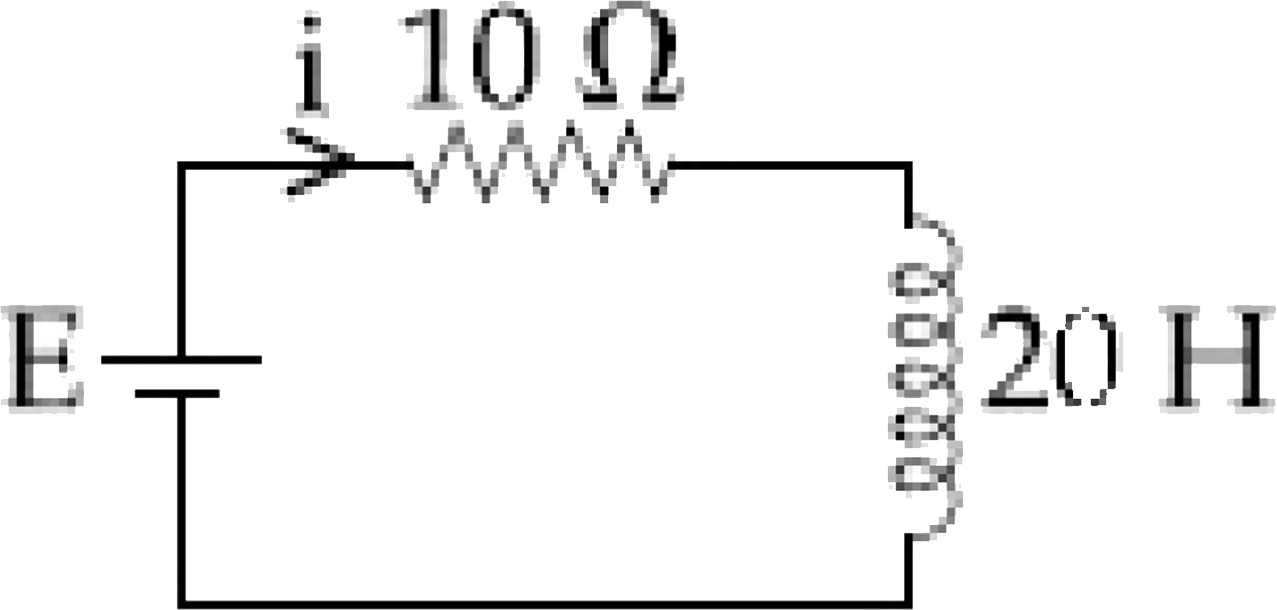
View SolutionAn inductor of 2 H and a resistance of 10Ω are connects in series with a battery of 5 V. The initial rate of change of current is
View SolutionA coil has inductance of 115πH and is joined in series with a resistance of 220Ω. When an alternating emf of 220V at 50Hz is applied to it, then the wattless component of the current in the circuit is
View SolutionAn inductor of inducance 5.0 H, having a negligible resistance, is connected in series with a 100Ω resistor and a battery of emf 2.0 V. Find the potential difference across the resistor 20 ms after the circuit is switched on.
View SolutionA circuit is set up by connecting L=100mH, C=5μF and R=100Ω in series. An alternating emf of 150√2 )V,(500)/(pi) Hz is applied across this series combination.Calculate the impedance of the circuit. What is the average power dissipated in the resistor
View SolutionA cell of 1.5V is connected across an inductor of 2mH in series with a 2 Ω resistor What is the rate of growth of current immediately after the cell is switched on.
View Solution
