The nuclear charge (Ze) is non uniformlly distribute with in a nucleus of radius r. The charge density ρ(r) (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
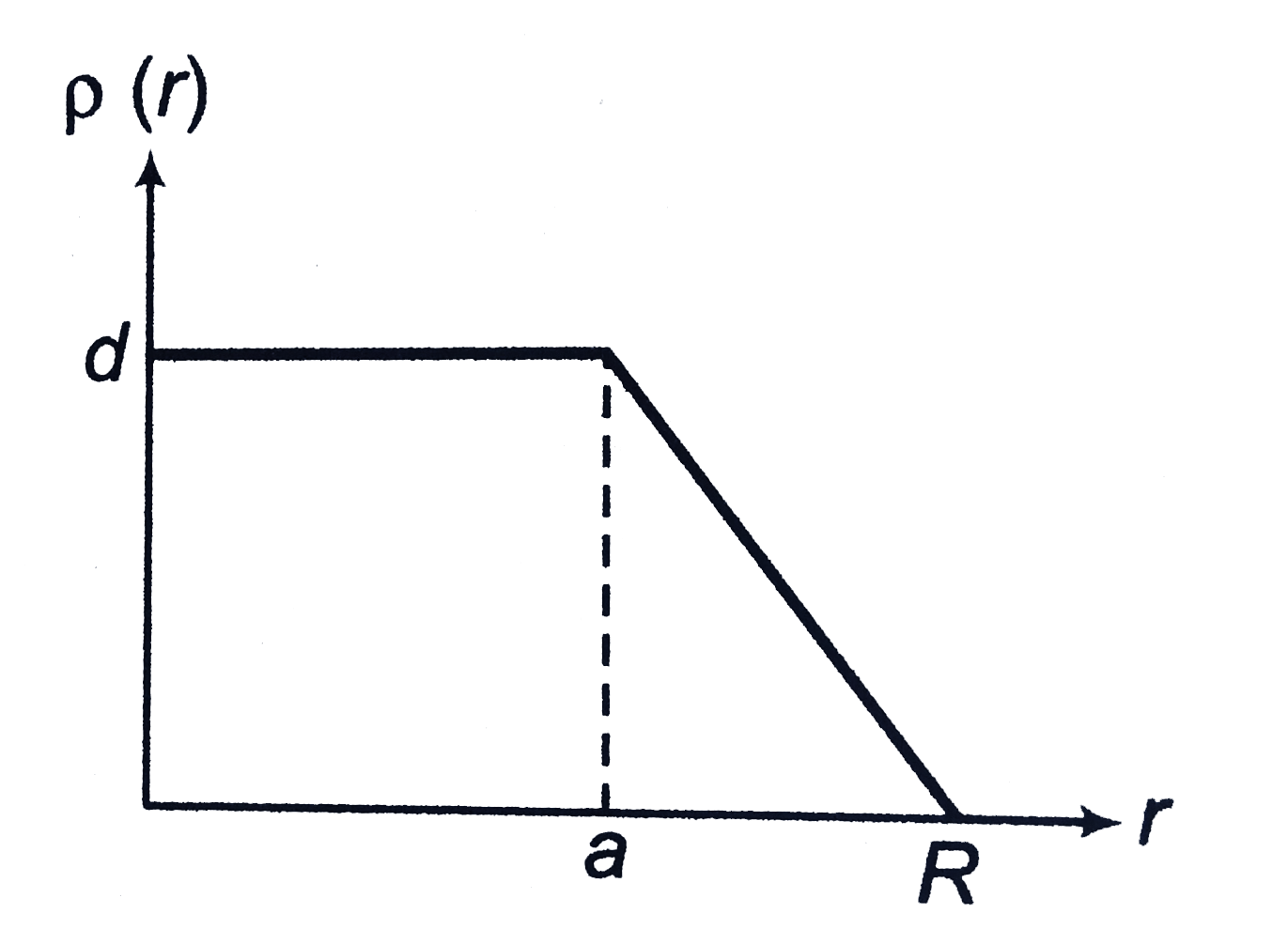
For a=0 the value of d (maximum value of ρ as shown in the figure) is

3Ze4πR3
3ZeπR3
4Ze3πR3
Ze3πR3
The correct Answer is:B
For a=0,
ρ(r)=(−dR.r+d)
Now, ∫R0(4πr2)(d−dRr)dr=net charge =Ze
Solving this equation we get d=3ZeπR3

Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.1
4 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.2
9 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 8
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
The nuclear charge (Ze) is non uniformlly distribute with in a nucleus of radius r. The charge densilty ρ(r) (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
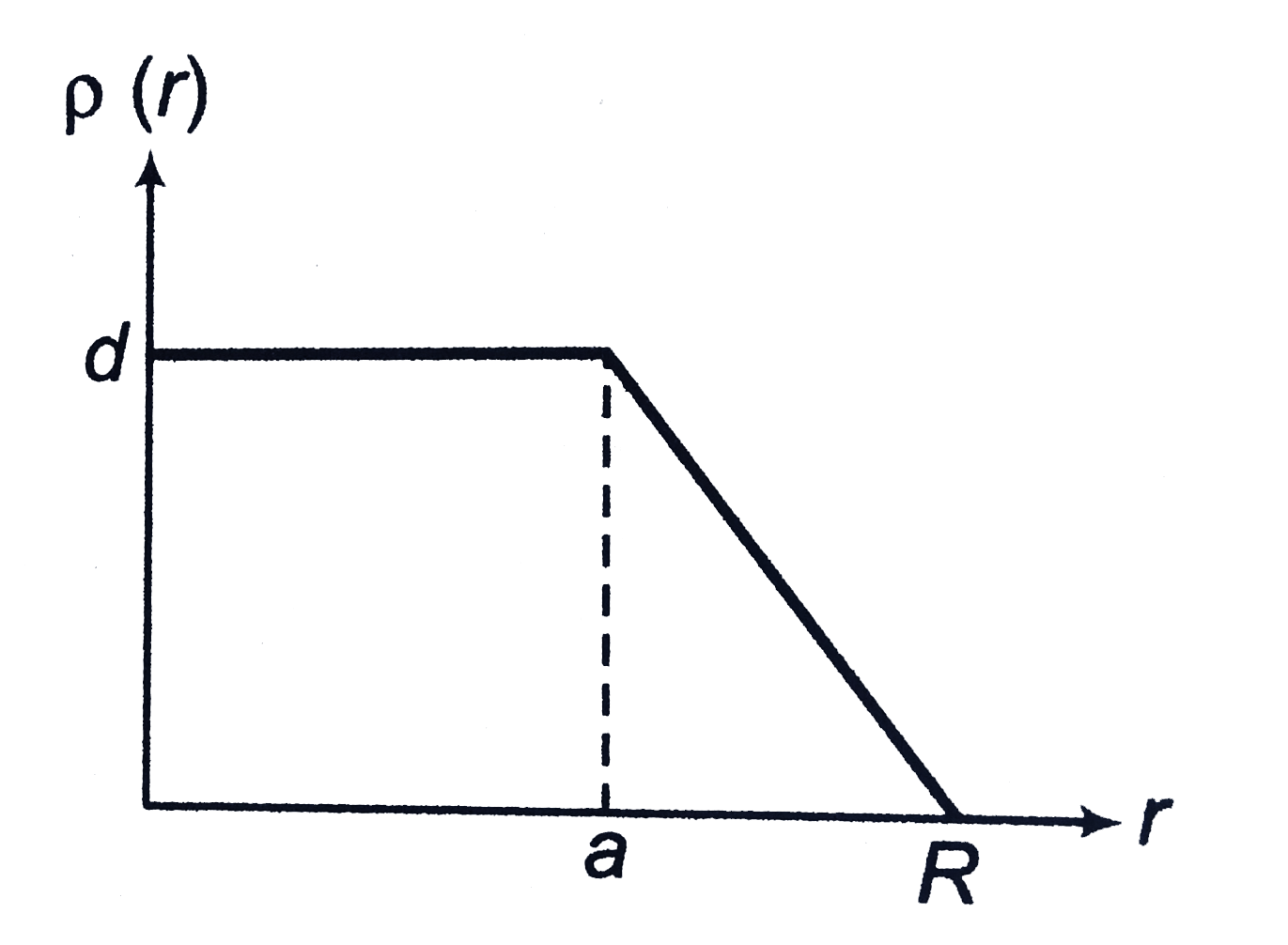
The electric field within the nucleus is generaly observed to be linearly dependent on r. This implies
View SolutionThe nuclear charge (Ze) is non uniformlly distribute with in a nucleus of radius r. The charge densilty ρ(r) (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.

The electric field within the nucleus is generaly observed to be linearly dependent on r. This implies
View SolutionA charge +Q, is uniformaly distributed within a sphere of radius R. Find the electric field, due to this charge distribution, at a point distant r form the centre of the spehre where :
(i) 0<r<R and
(ii)r>R
View Solution3 charges are placed in a circle of radius d as shown in figure. Find the electric field along x-axis at centre of circle.

View Solution3 charges are placed in a circle of radius d as shown in figure. Find the electric field along x-axis at centre of circle.

View SolutionFind the electric field caused by a disc of radius a with a uniform surfce charge density σ (charge per unit area) at a point along the axis of the disc a distance x from its centre.
View SolutionAn uncharged metallic solid sphere of radius R is placed at a distance 2R from point charge Q as shown in figure. The electric field intensity due to induced charge at centre of sphere is
View SolutionInside a uniformly charged infinitely long cylinder of radius 'R' and volume charge density 'rho' there is a spherical cavity of radius 'R//2'. A point 'P' is located at a dsintance 2R from the axis of the cylinder as shown. Then the electric field strength at the point 'P' is
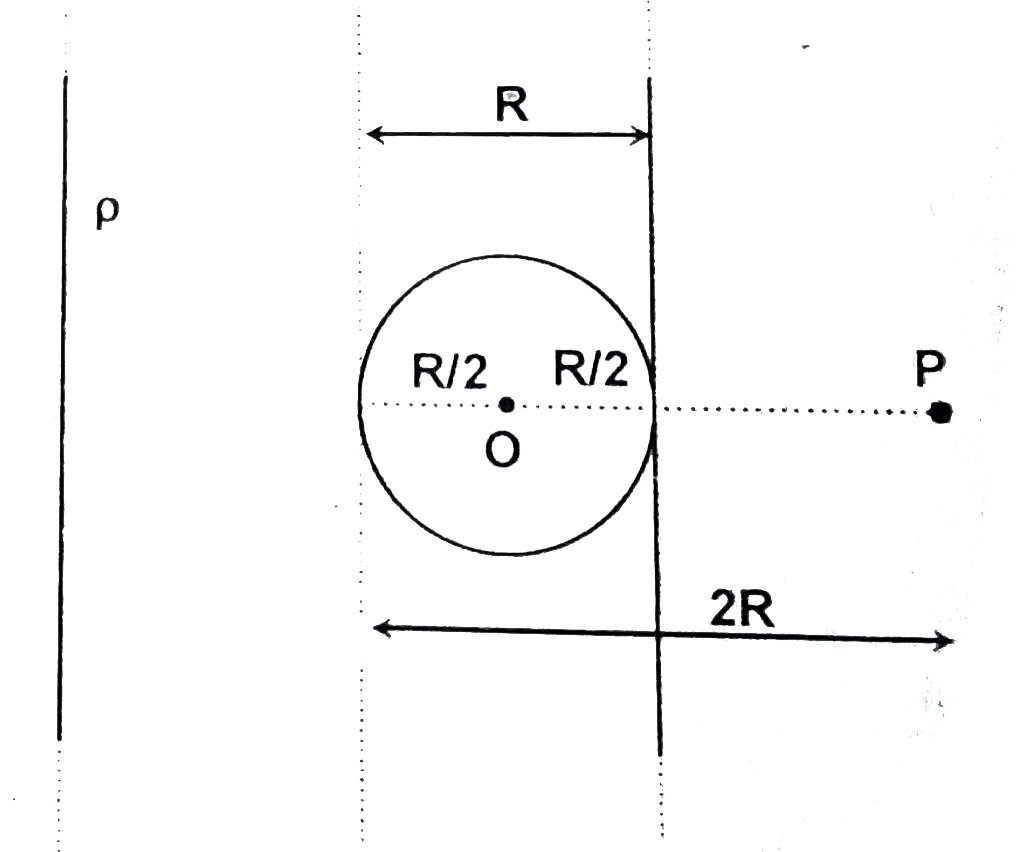
View SolutionAn isolated solid metal sphere of radius R is given an electric charge. The variation of the intensity of the electric field with the distance r from the centre of the sphere is best shown by
View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View Solution
