The temperature of n-moles of an ideal gas is increased from T0 to 2T0 through a process p=αT. Find work done in this process.
The correct Answer is:B
To find the work done during the process where the temperature of n moles of an ideal gas is increased from T0 to 2T0 under the condition p=αT, we can follow these steps:
1. Use the Ideal Gas Law:
The ideal gas law states that:
PV=nRT
Given that pressure p is defined as p=αT, we can substitute this into the ideal gas equation.
2. Express Volume in Terms of Temperature:
Substitute p into the ideal gas equation:
αT⋅V=nRT
Rearranging gives:
V=nRT2α
3. Differentiate Volume with Respect to Temperature:
To find dV, differentiate V with respect to T:
dV=ddT(nRT2α)=2nRTαdT
4. Set Up the Work Done Integral:
The work done W during a process is given by:
W=∫VfVipdV
Substitute p=αT and dV=2nRTαdT:
W=∫2T0T0αT⋅2nRTαdT
5. Simplify the Integral:
The α terms cancel out:
W=∫2T0T02nRdT
6. Evaluate the Integral:
The integral simplifies to:
W=2nR(T)2T0T0=2nR(2T0−T0)=2nRT0
7. Final Result:
Thus, the work done in this process is:
W=2nRT0
The ideal gas law states that:
PV=nRT
Given that pressure p is defined as p=αT, we can substitute this into the ideal gas equation.
Substitute p into the ideal gas equation:
αT⋅V=nRT
Rearranging gives:
V=nRT2α
To find dV, differentiate V with respect to T:
dV=ddT(nRT2α)=2nRTαdT
The work done W during a process is given by:
W=∫VfVipdV
Substitute p=αT and dV=2nRTαdT:
W=∫2T0T0αT⋅2nRTαdT
The α terms cancel out:
W=∫2T0T02nRdT
The integral simplifies to:
W=2nR(T)2T0T0=2nR(2T0−T0)=2nRT0
Thus, the work done in this process is:
W=2nRT0
Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Example Type 1
2 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Example Type 2
1 Video
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
Similar Questions
Temperature of two moles of an ideal gas is increased by 300K in a process V=aT, where a is positive constant. Find work done by the gas in the given process.
View SolutionPressure and volume of a gas changes from (p0V0) to (p04,2V0) in a process pV2= constant. Find work done by the gas in the given process.
View Solution
Knowledge Check
The temperature of n moles of an ideal gas is increased from T to 4T through a process for which pressure P=aT−1 where a is a constant .Then the work done by the gas is
Aa. nRTBb. 4nRTCc. 2nRTDd. 6nRT
Temperature of a monoatomic gas is increased from T0 to 2T0 in three different processes:
isochoric, isobaric and adiabatic. Heat given to the gas in these three processes are Q1,Q2andQ3 respectively. Then, choose the correct option.
View SolutionTwo moles of a monoatomic ideal gas undergoes a process AB as shown in the figure. Then, find the work done during the process in Joule.
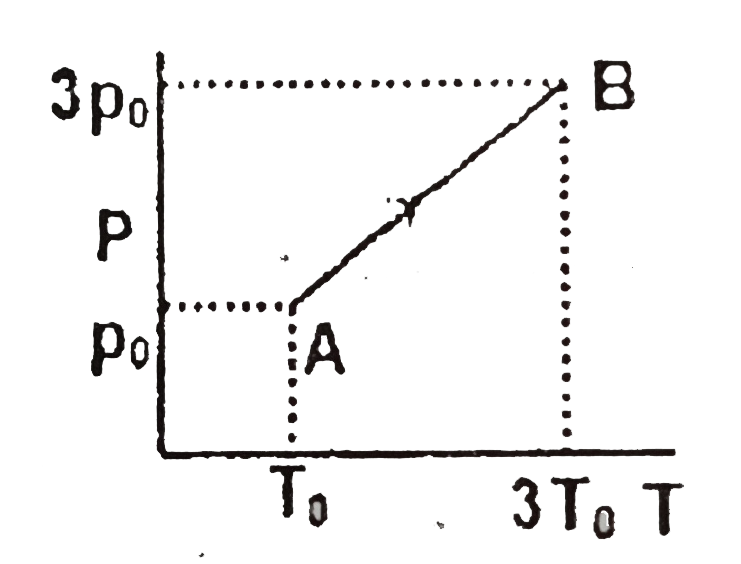
View SolutionIn a process V∝T2, temperature of 2 moles of a gas is increased by 200K. Work done by the gas in this process will be
View SolutionThe state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is p02, then the pressure of the gas in state C is
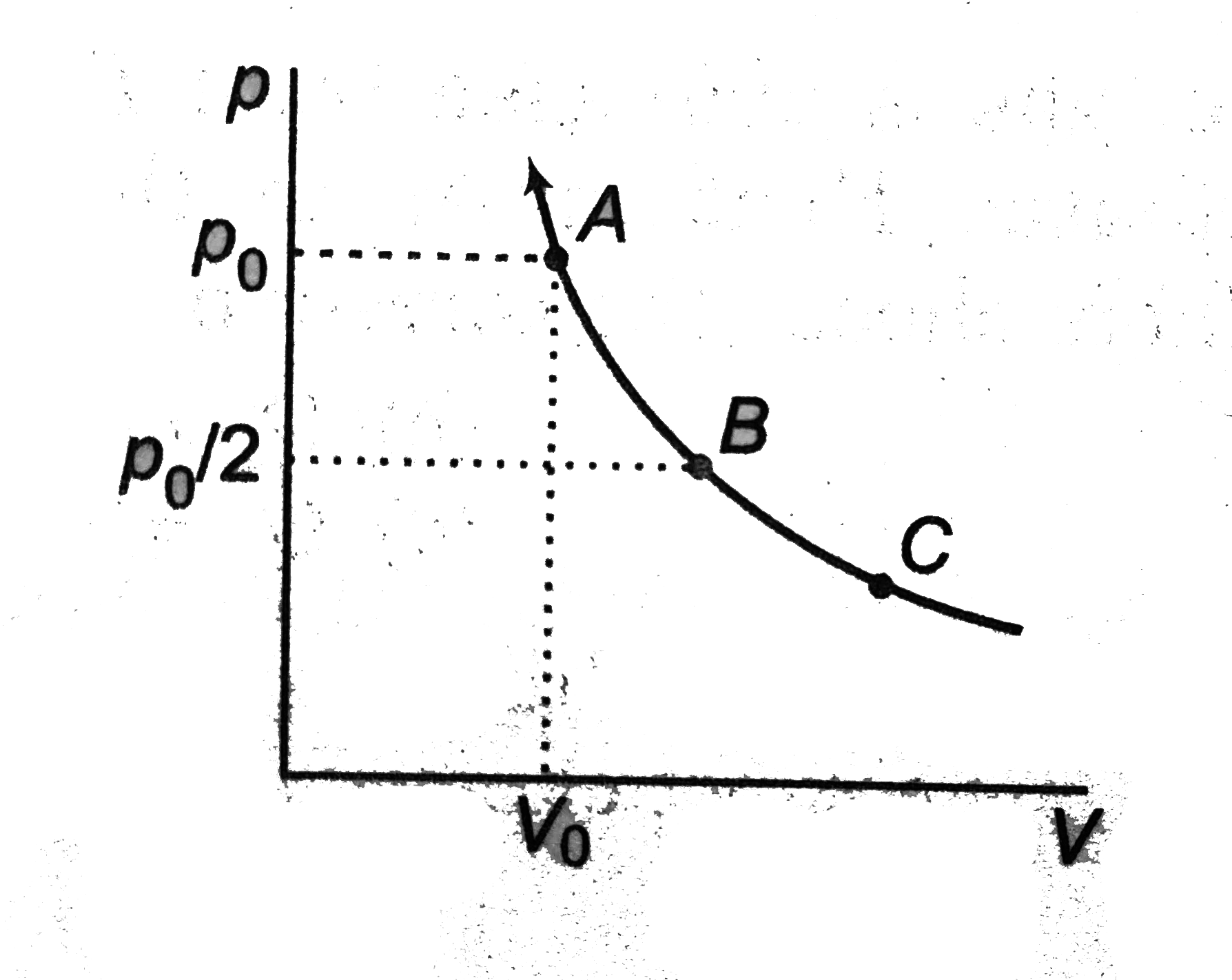
View SolutionThe state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is p02, then the pressure of the gas in state C is

View SolutionThe temperature (T) of one mole of an ideal gas varies with its volume (V) as T=−αV3+βV2, where αandβ are positive constants. The maximum pressure of gas during this process is
View SolutionOne mole of an ideal gas undergoes a process such that P∝1T. The molar heat capacity of this process is 4R.
View Solution
