An ideal gas (CpCv=γ) is taken through a process in which the pressure and volume vary as (p=aVb). Find the value of b for which the specific heat capacity in the process is zero.
The correct Answer is:A
To find the value of b for which the specific heat capacity in the process is zero, we can follow these steps:
Step 1: Understand the relationship between heat transfer, internal energy, and work done
From the first law of thermodynamics, we know:
dQ=dU+dW
where dQ is the heat added to the system, dU is the change in internal energy, and dW is the work done by the system.
Step 2: Express heat transfer and internal energy for an ideal gas
For an ideal gas, the heat added can be expressed as:
dQ=nCpdT
and the change in internal energy is given by:
dU=nCvdT
Step 3: Set the condition for specific heat capacity being zero
If the specific heat capacity CB in the process is zero, then:
dQ=0
This implies:
nCpdT=0
For this to hold true, either n=0 (which is not the case) or dT=0. If dT=0, it indicates that the temperature does not change, suggesting an isothermal process.
Step 4: Consider the implications of dQ=0
If dQ=0, it indicates that the process is adiabatic. For an adiabatic process, we have the relation:
PVγ=constant
Step 5: Relate the given pressure-volume relationship to the adiabatic condition
Given the relationship p=aVb, we can express it in terms of the adiabatic condition:
PVγ=k(constant)
This means:
pVγ=k
Comparing this with the given equation p=aVb, we can rewrite it as:
p=kVγ
This leads us to:
aVb=kVγ
Step 6: Equate the powers of V
From the equation aVb=kVγ, we can equate the powers of V:
b=−γ
Conclusion
Thus, the value of b for which the specific heat capacity in the process is zero is:
−γ
From the first law of thermodynamics, we know:
dQ=dU+dW
where dQ is the heat added to the system, dU is the change in internal energy, and dW is the work done by the system.
For an ideal gas, the heat added can be expressed as:
dQ=nCpdT
and the change in internal energy is given by:
dU=nCvdT
If the specific heat capacity CB in the process is zero, then:
dQ=0
This implies:
nCpdT=0
For this to hold true, either n=0 (which is not the case) or dT=0. If dT=0, it indicates that the temperature does not change, suggesting an isothermal process.
If dQ=0, it indicates that the process is adiabatic. For an adiabatic process, we have the relation:
PVγ=constant
Given the relationship p=aVb, we can express it in terms of the adiabatic condition:
PVγ=k(constant)
This means:
pVγ=k
Comparing this with the given equation p=aVb, we can rewrite it as:
p=kVγ
This leads us to:
aVb=kVγ
From the equation aVb=kVγ, we can equate the powers of V:
b=−γ
Thus, the value of b for which the specific heat capacity in the process is zero is:
−γ
Topper's Solved these Questions
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBook:DC PANDEY ENGLISHChapter:THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESExercise:Level 2 Single Correct
Explore 12 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBook:DC PANDEY ENGLISHChapter:THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESExercise:Level 2 More Than One Correct
Explore 7 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBook:DC PANDEY ENGLISHChapter:THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESExercise:Level 1 Objective
Explore 10 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBook:DC PANDEY ENGLISHChapter:THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESExercise:Medical entrance gallary
Explore 30 Videos
- UNIT AND DIMENSIONSBook:DC PANDEY ENGLISHChapter:UNIT AND DIMENSIONSExercise:Assertion And Reason
Explore 2 Videos
Similar Questions
An ideal gas is taken through a process in which pressure and volume vary as P=kV2. Show that the molar heat capacity of the gas for the process is given by C=Cv+R3.
View SolutionAn ideal gas is taken through a process in which the pressure and the volume are changed according to the equation p=kv. Show that the molar heat capacity of the gas for the process is given by (C=Cv+R2).
View SolutionAn ideal gas is taken through a process in which the pressure and the volume are changed according to the equation p=kv. Show that the molar heat capacity of the gas for the process is given by (C=Cv+R2).
View SolutionFor an ideal gas, the specific heat capacity during an isentropic process is always
View SolutionA gas undergoes a process in which its pressure P and volume V are related as VP = constant. The bulk modulus of gas for this process
View SolutionFind the value of molar heat capacity for an ideal gas in an adiabatic process.
View SolutionA monoatomic gas undergoes a process in which the pressure (P) and the volume (V) of the gas are related as PV−3=constant. What will be the molar heat capacity of gas for this process?
View SolutionAn ideal gas (γ=1.5) undergoes a thermodynamic process in which the temperature and pressure of the gas are related as T−1P2= constant. The molar heat capacity of the gas during the process is
View SolutionAn ideal gas (γ=1.67) is taken through the process abc shown in figure . The temperature at the point a is 300k. Calculate (a) the temperature at b and c, (b) the work done in the process, ( c) the amount of heat supplied in the path ab and in the path bc and (d) the change in the internal energy of the gas in the process.
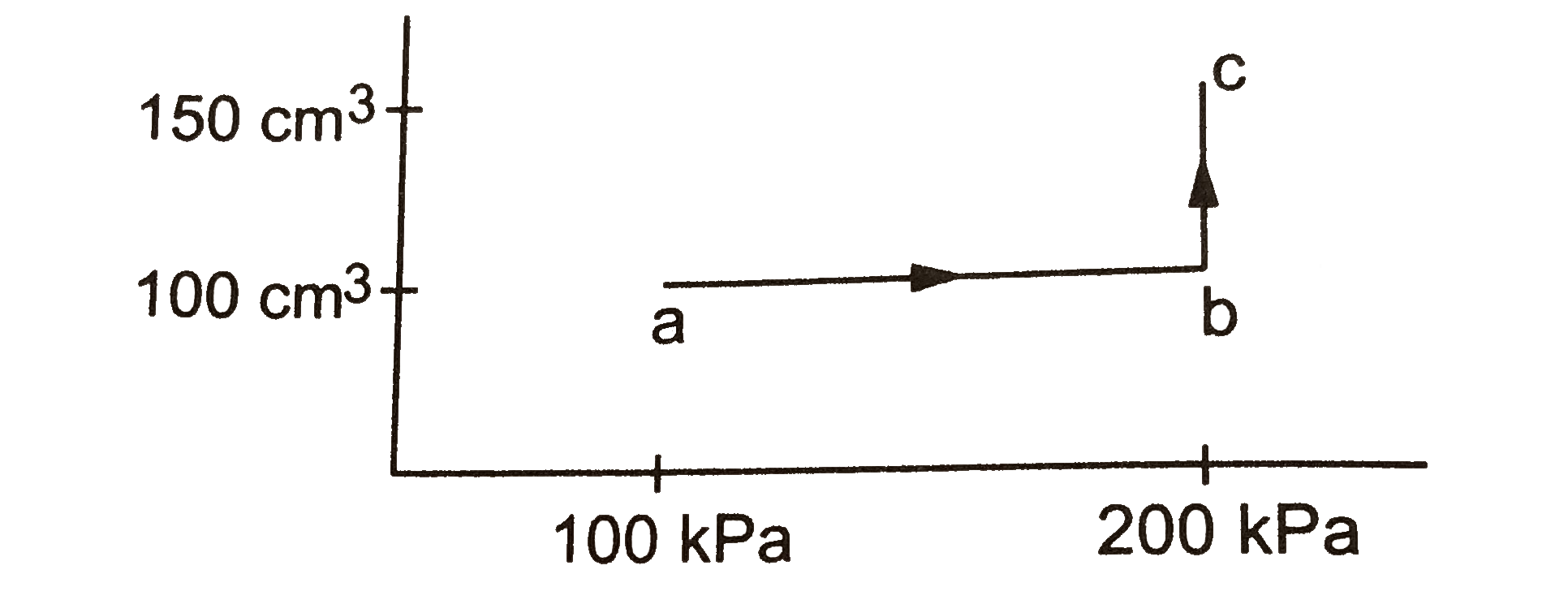
View SolutionThe variation of pressure versus volume is shown in the figure. The gas is diatomic and the molar specific heat capacity for the process is found to xR. Find the value of x.
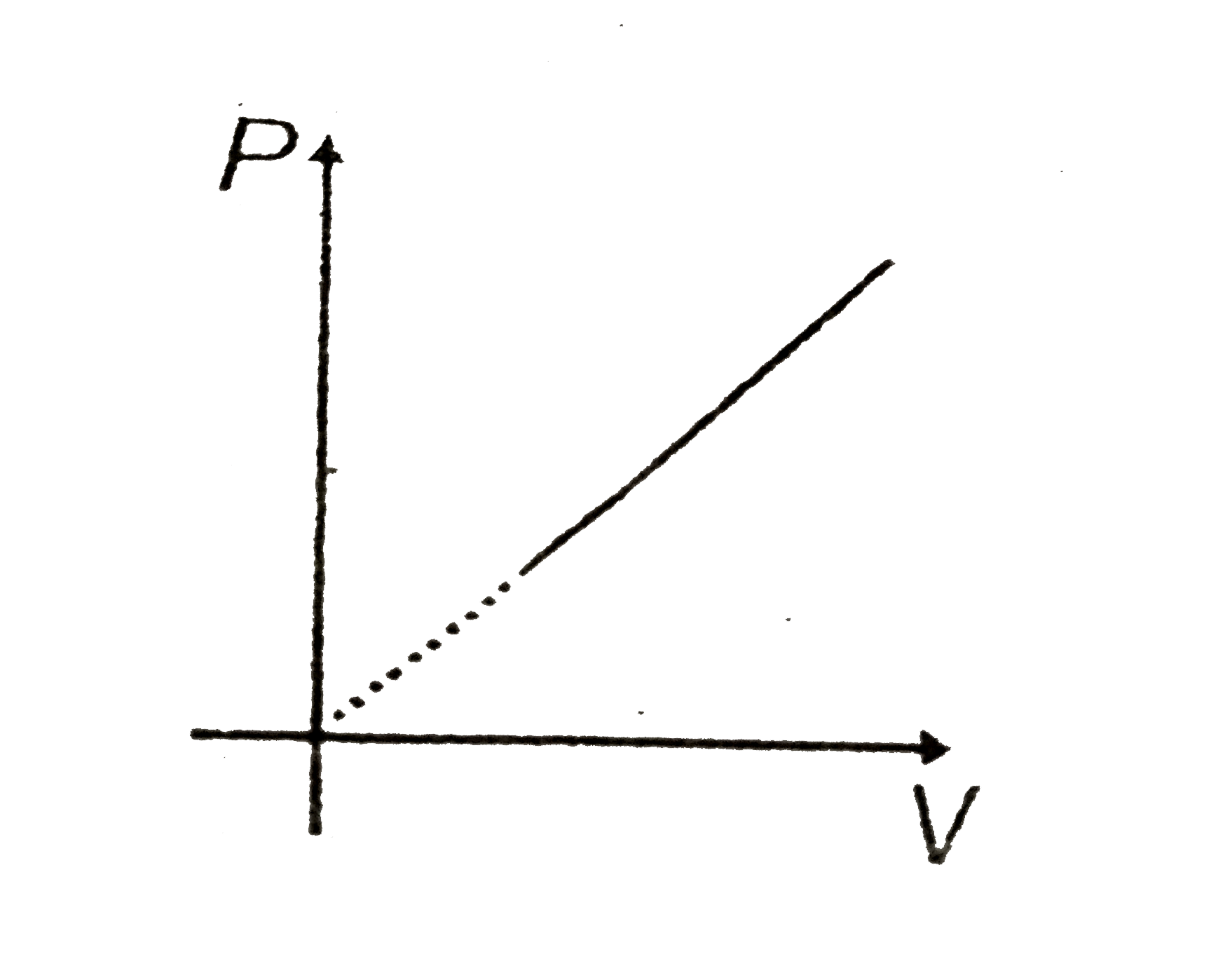 .
.
View Solution

