An ideal gas is taken through a process in which the pressure and the volume are changed according to the equation p=kv. Show that the molar heat capacity of the gas for the process is given by (C=Cv+R2).
The correct Answer is:A
To solve the problem, we need to derive the expression for the molar heat capacity C of an ideal gas undergoing a process defined by the equation p=kV. Here’s a step-by-step solution:
Step 1: Start with the Ideal Gas Law
The ideal gas law is given by:
PV=nRT
For one mole of gas (n=1), this simplifies to:
PV=RT
Step 2: Substitute the given relationship p=kV
From the problem, we have:
p=kV
Substituting this into the ideal gas law gives:
(kV)V=RT
This simplifies to:
kV2=RT
Step 3: Differentiate with respect to T
We differentiate both sides of the equation kV2=RT with respect to T:
ddT(kV2)=ddT(RT)
Using the product rule on the left side, we get:
k⋅2VdVdT=R
This can be rearranged to find dVdT:
dVdT=R2kV
Step 4: Apply the First Law of Thermodynamics
According to the first law of thermodynamics:
dQ=dU+dW
For one mole of gas, the change in internal energy dU is given by:
dU=CvdT
The work done dW during an expansion is:
dW=pdV
Substituting p=kV gives:
dW=kVdV
Step 5: Substitute dW and dU into the First Law
Now we can write:
dQ=CvdT+kVdV
Substituting dV from Step 3:
dQ=CvdT+kV(R2kV)dT
This simplifies to:
dQ=CvdT+R2dT
Step 6: Factor out dT to find C
Factoring dT out gives:
dQ=(Cv+R2)dT
Thus, the molar heat capacity C for the process is:
C=Cv+R2
Conclusion
We have shown that the molar heat capacity of the gas for the process is given by:
C=Cv+R2
The ideal gas law is given by:
PV=nRT
For one mole of gas (n=1), this simplifies to:
PV=RT
From the problem, we have:
p=kV
Substituting this into the ideal gas law gives:
(kV)V=RT
This simplifies to:
kV2=RT
We differentiate both sides of the equation kV2=RT with respect to T:
ddT(kV2)=ddT(RT)
Using the product rule on the left side, we get:
k⋅2VdVdT=R
This can be rearranged to find dVdT:
dVdT=R2kV
According to the first law of thermodynamics:
dQ=dU+dW
For one mole of gas, the change in internal energy dU is given by:
dU=CvdT
The work done dW during an expansion is:
dW=pdV
Substituting p=kV gives:
dW=kVdV
Now we can write:
dQ=CvdT+kVdV
Substituting dV from Step 3:
dQ=CvdT+kV(R2kV)dT
This simplifies to:
dQ=CvdT+R2dT
Factoring dT out gives:
dQ=(Cv+R2)dT
Thus, the molar heat capacity C for the process is:
C=Cv+R2
We have shown that the molar heat capacity of the gas for the process is given by:
C=Cv+R2
Topper's Solved these Questions
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Single Correct
12 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 More Than One Correct
7 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 1 Objective
10 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary
30 Videos
- UNIT AND DIMENSIONSBOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason
2 Videos
Similar Questions
An ideal gas is taken through a process in which pressure and volume vary as P=kV2. Show that the molar heat capacity of the gas for the process is given by C=Cv+R3.
View SolutionFor a certain process, pressure of diatomic gas varies according to the relation P=aV2, where a is constant. What is the molar heat capacity of the gas for this process ?
View SolutionAn ideal gas (CpCv=γ) is taken through a process in which the pressure and volume vary as (p=aVb). Find the value of b for which the specific heat capacity in the process is zero.
View SolutionAn ideal gas (CpCv=γ) is taken through a process in which the pressure and volume vary as (p=aVb). Find the value of b for which the specific heat capacity in the process is zero.
View SolutionA monoatomic gas undergoes a process in which the pressure (P) and the volume (V) of the gas are related as PV−3=constant. What will be the molar heat capacity of gas for this process?
View SolutionAn ideal gas with adiabatic exponent γ=43 undergoes a process in which internal energy is related to volume as U=V2 . Then molar heat capacity of the gas for the process is :
View Solutionan ideal diatomic gas undergoes a polytropic process described by the equation P√V=constant . The molar heat capacity of the gas during this process is
View SolutionAn ideal gas (γ=1.5) undergoes a thermodynamic process in which the temperature and pressure of the gas are related as T−1P2= constant. The molar heat capacity of the gas during the process is
View SolutionIn a thermodynamic process on an ideal diatomic gas, work done by the gas is η times the heat supplied (η<1). The molar heat capacity of the gas for the process is
View SolutionAn ideal gas undergoes a process P→Q→R as shown in pressure (p) - volume (v) diagram.The work done by the gas is
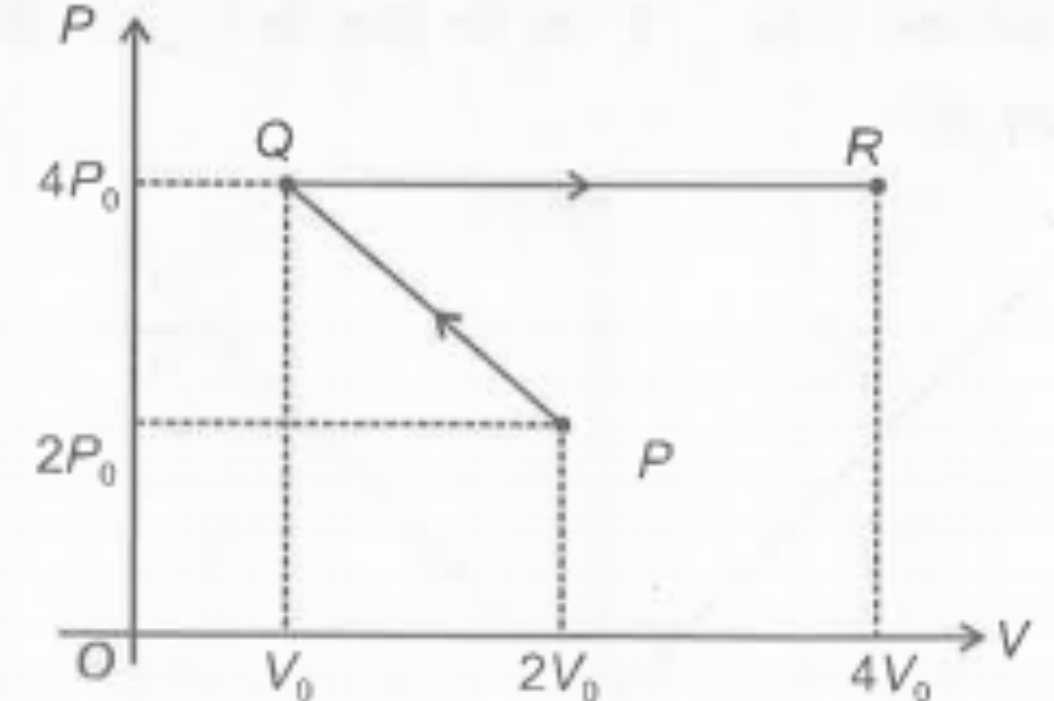
View Solution
