An ideal gas is taken through the process abc shown in figure . The temperature at the point a is . Calculate (a) the temperature at b and c, (b) the work done in the process, ( c) the amount of heat supplied in the path ab and in the path bc and (d) the change in the internal energy of the gas in the process.
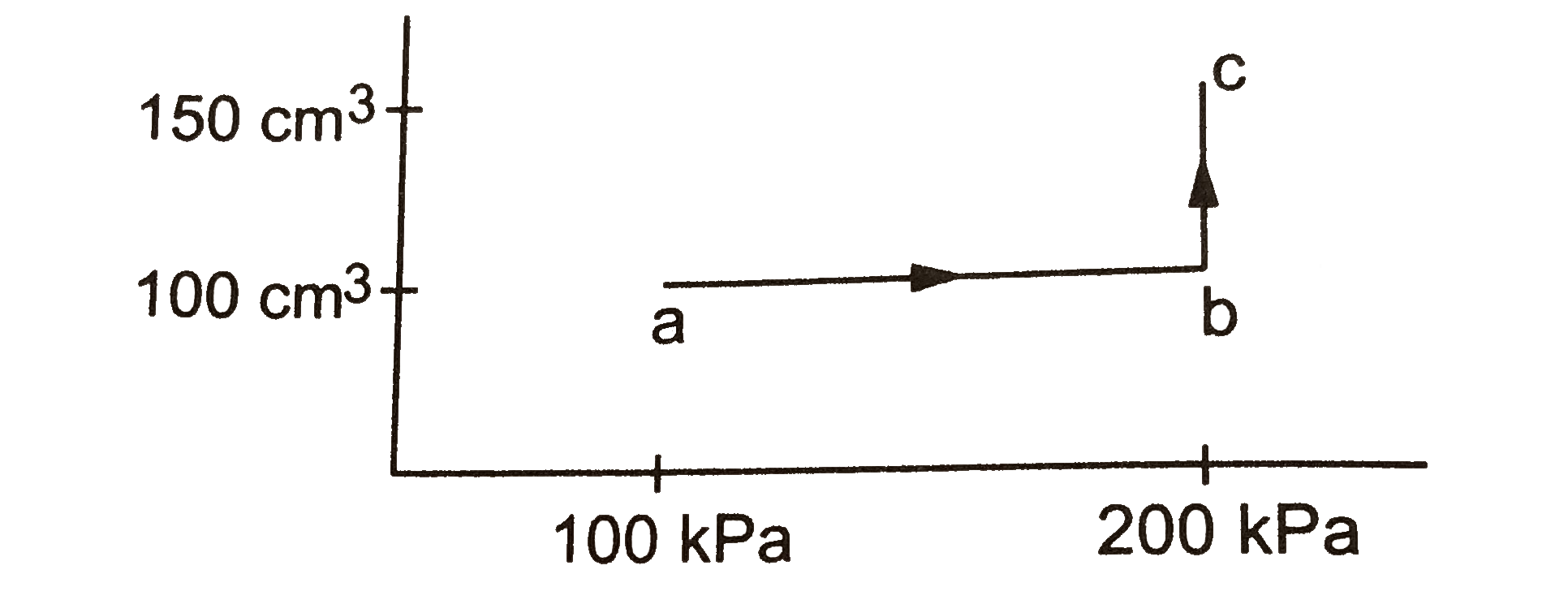
(a) For a, b 'V' is constant
So,
implies
For b, c 'p' is constant
So,
implies
implies
(b) Work done = Area enclosed under the graph
.
(c) 'Q' supplied
Now,
=14.925( :. gamma = 1.67)bc = nCpdTC_p=(gammaR)/(gamma-1)=(PV)/(RT) xx (gammaR)/(gamma-1) xxdT=(200xx10^(3) xx 150 xx 10^(-6))/(600xx0.67)xx 300=10xx(1.67)/(0.67)=24.925Q= DeltaU+WDeltaU=Q-W=(24.925 + 14. 925)-10=39.850-10=29.850J.
Topper's Solved these Questions
Similar Questions
Ideal gas is taken through the process shown in the figure :
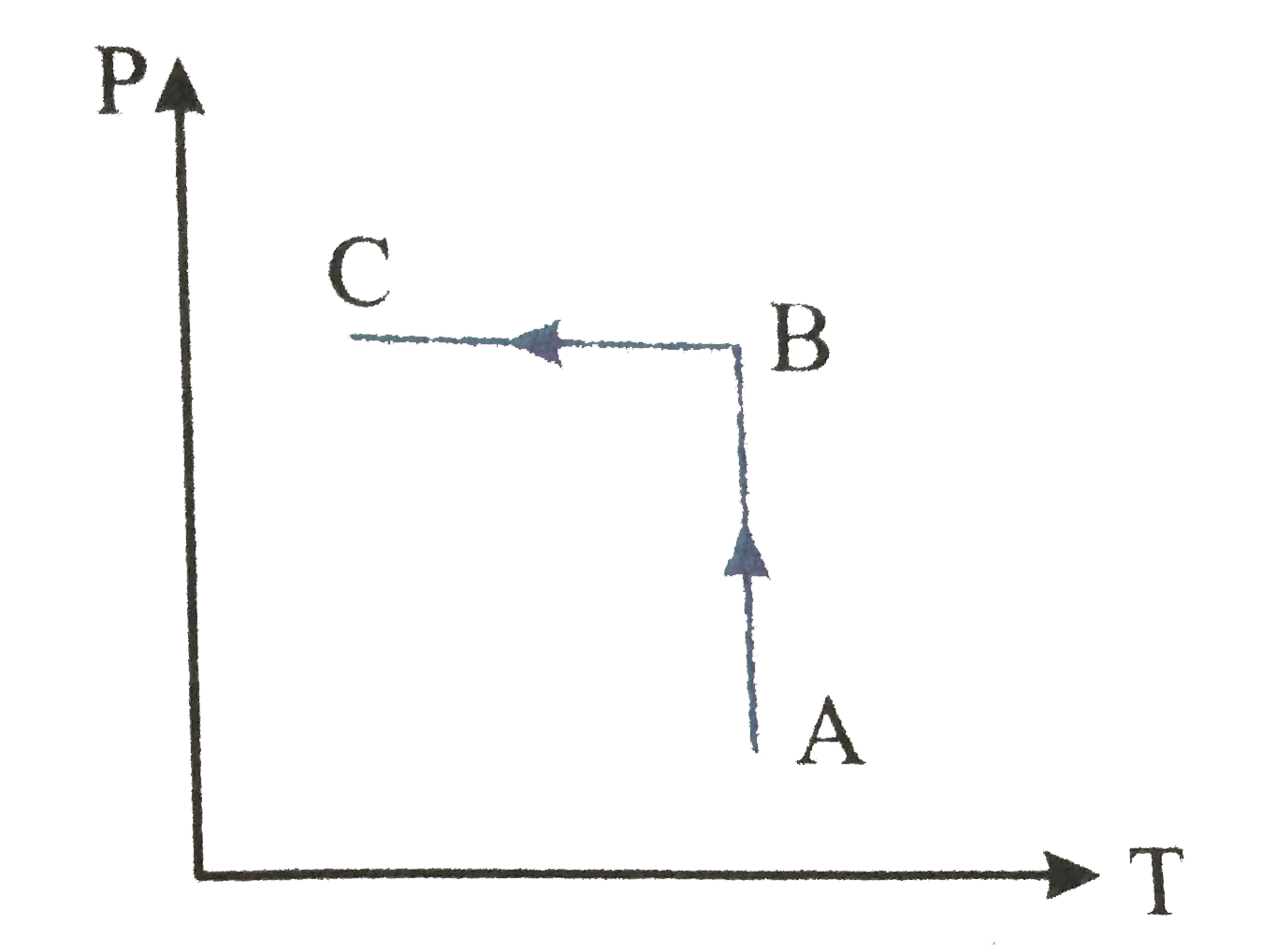
View SolutionIdeal gas is taken through the process shown in the figure :

View SolutionA sample of ideal gas is taken through the cyclic process shown in the figure. The temerauture of the gas in state A is TA =200 K. In states B and C the temperature of the gas is the same.
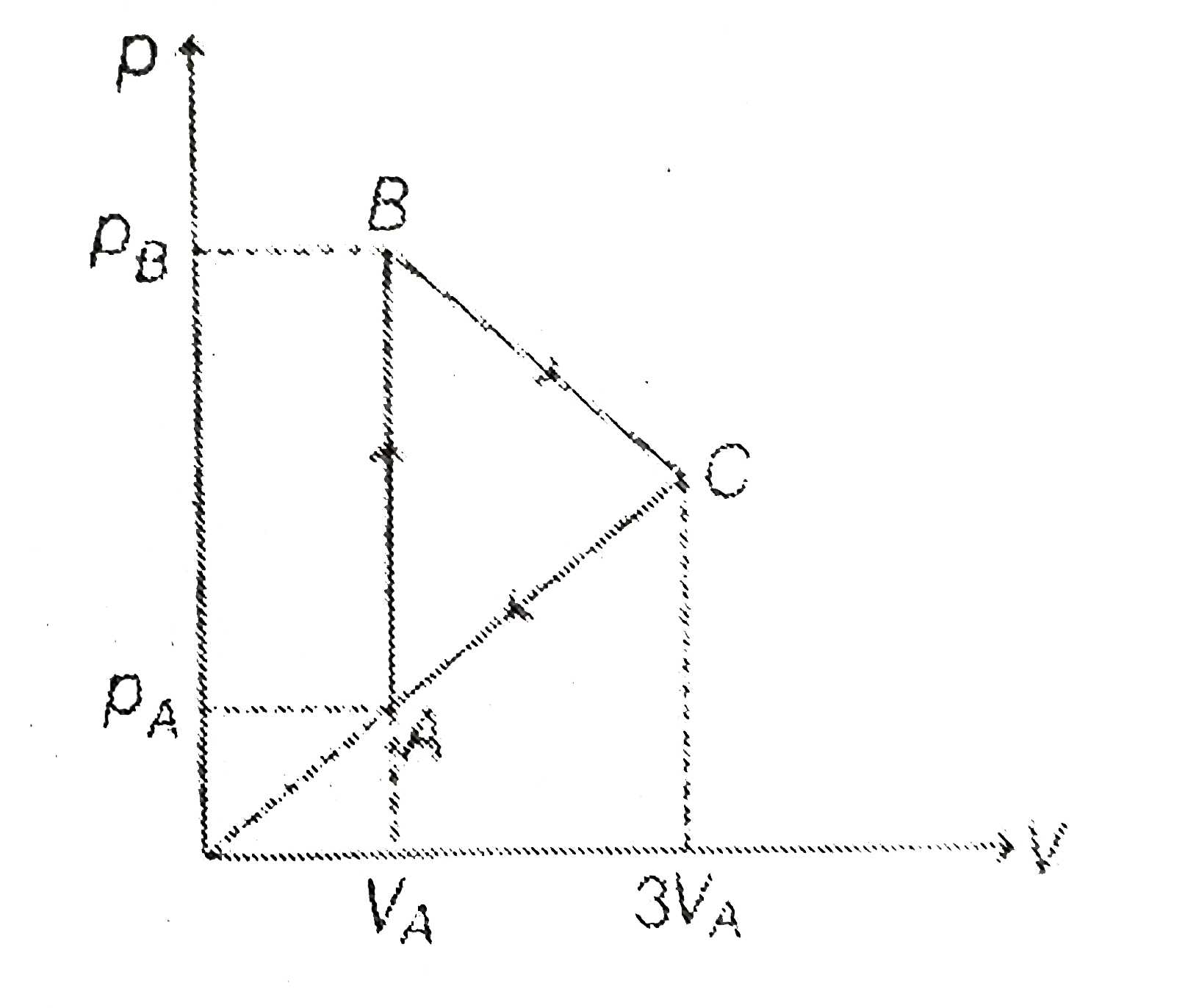
Net work done by the gas in the process is
View SolutionA mono-atomic gas is taken along path AB as shown. Calculate change in internal energy of the gas.
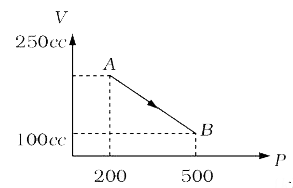
View SolutionHalf mole of an ideal gas (γ=53) is taken through the cycle abcda as shown in figure . Take (R=253JK−1mol−1). (a) Find the temperature of the gas in the states a, b, c and d. (b) Find the amount of heat supplied in the processes ab and bc. (c ) Find the amount of heat liberated in the processes cdandda.
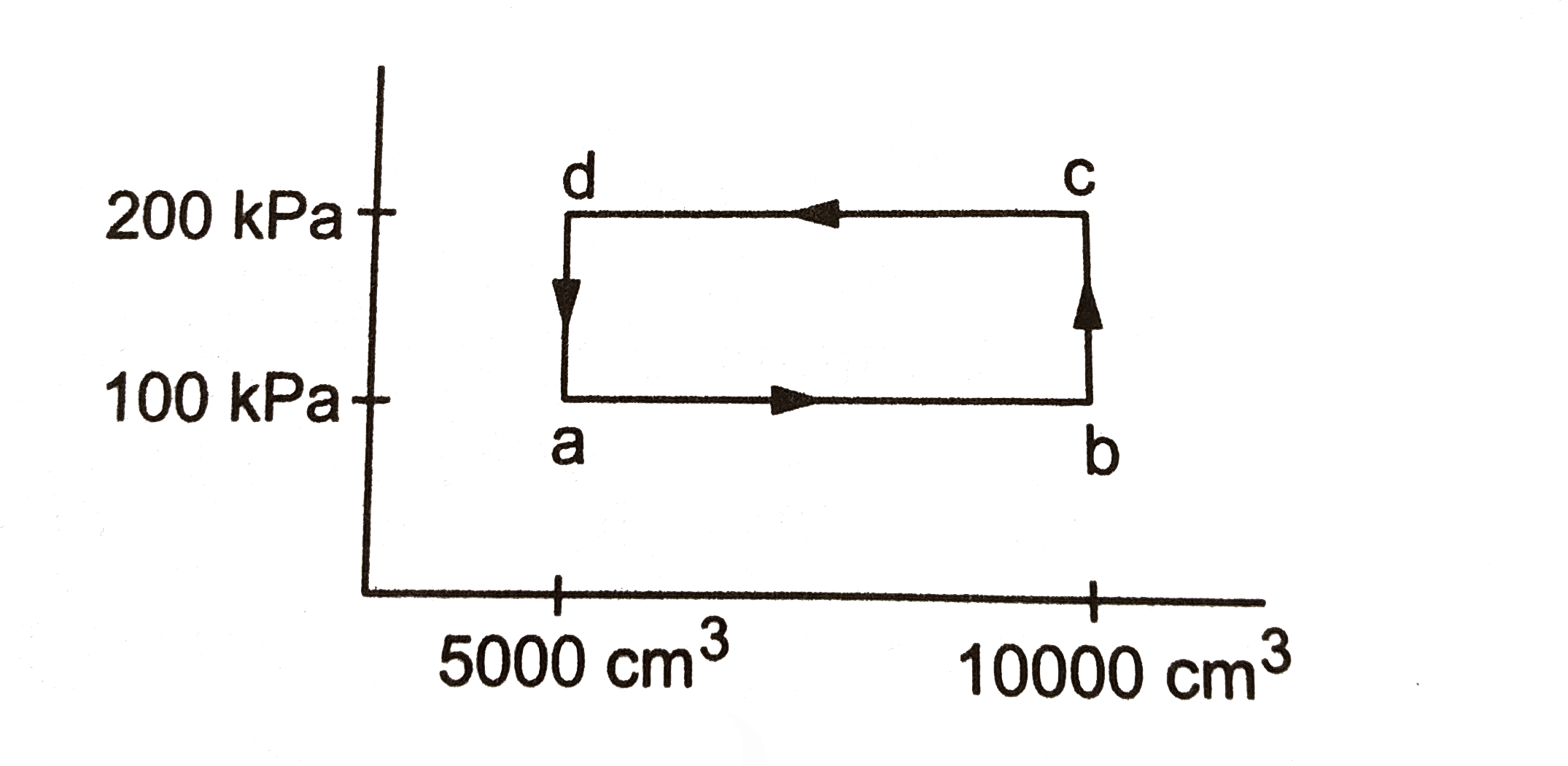
View SolutionIn a cyclic process shown in the figure an ideal gas is adiabatically taken from BtoA, the work done on the gas during the process BtoA is 30,J when the gas is taken from A to B the heat absorbed by the gas is 20J Then change in internal energy of the gas in the process A to B is :

View SolutionIn a cyclic process shown in the figure an ideal gas is adiabatically taken from BtoA, the work done on the gas during the process BtoA is 30,J when the gas is taken from A to B the heat absorbed by the gas is 20J Then change in internal energy of the gas in the process A to B is :

View SolutionIn a cyclic process shown in the figure an ideal gas is adiabatically taken from BtoA, the work done on the gas during the process BtoA is 30,J when the gas is taken from A to B the heat absorbed by the gas is 20J Then change in internal energy of the gas in the process A to B is :

View SolutionA gas is taken along the path AB as shown in fig, if 70 cal of heat is extracted from the gas in the process, calculate the change in the internal energy of the system.
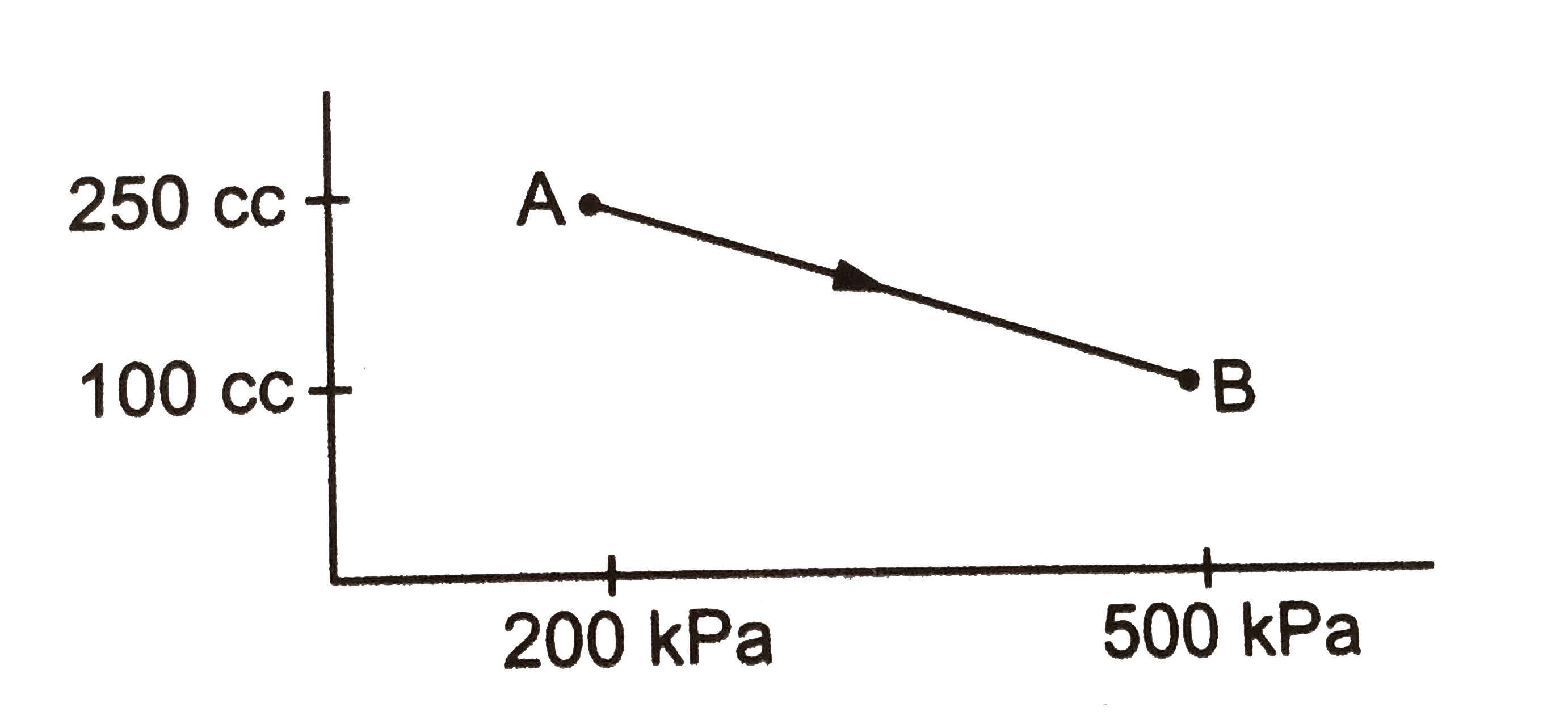
View SolutionOne mole of an ideal monatomic gas is taken round the cyclic process ABCA as shown in figure. Calculate
(a) the work done by the gas.
(b) the heat rejected by the gas in the path CA and the heat absorbed by the gas in the path AB,
(c) the net heat absorbed by the gas in the path BC,
(d) the maximum temperature attained by the gas during the cycle.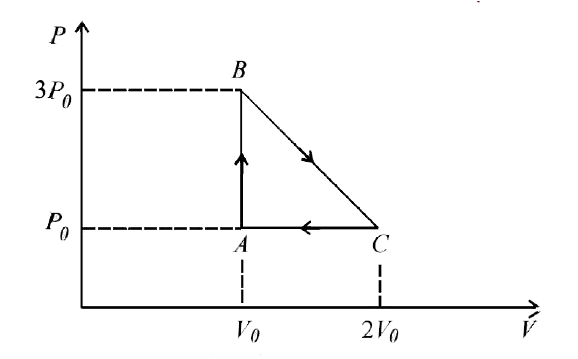
View Solution

