When tension of a string is increased by 2.5 N, the initial frequency is altered in the ratio of 3:2. The initial tension in the string is
6N
5N
4N
2N
The correct Answer is:D
To solve the problem, we need to find the initial tension in the string given that when the tension is increased by 2.5 N, the frequency changes in the ratio of 3:2.
1. Define Variables:
Let the initial tension in the string be T (in Newtons). The initial frequency is denoted as f.
2. Frequency Relation:
The frequency of a vibrating string is given by the formula:
f=12L√Tμ
where L is the length of the string and μ is the linear mass density of the string.
3. New Tension and Frequency:
When the tension is increased by 2.5 N, the new tension becomes T+2.5 N. The new frequency is given as:
f′=12L√T+2.5μ
4. Frequency Ratio:
According to the problem, the ratio of the new frequency to the initial frequency is:
f′f=32
Substituting the expressions for f′ and f:
12L√T+2.5μ12L√Tμ=32
This simplifies to:
√T+2.5√T=32
5. Squaring Both Sides:
Squaring both sides to eliminate the square roots:
T+2.5T=(32)2
This gives:
T+2.5T=94
6. Cross-Multiplying:
Cross-multiplying gives:
4(T+2.5)=9T
7. Expanding and Rearranging:
Expanding the left side:
4T+10=9T
Rearranging gives:
10=9T−4T
Thus:
10=5T
8. Solving for T:
Dividing both sides by 5:
T=2 N
Final Answer:
The initial tension in the string is T=2 N.
---
Let the initial tension in the string be T (in Newtons). The initial frequency is denoted as f.
The frequency of a vibrating string is given by the formula:
f=12L√Tμ
where L is the length of the string and μ is the linear mass density of the string.
When the tension is increased by 2.5 N, the new tension becomes T+2.5 N. The new frequency is given as:
f′=12L√T+2.5μ
According to the problem, the ratio of the new frequency to the initial frequency is:
f′f=32
Substituting the expressions for f′ and f:
12L√T+2.5μ12L√Tμ=32
This simplifies to:
√T+2.5√T=32
Squaring both sides to eliminate the square roots:
T+2.5T=(32)2
This gives:
T+2.5T=94
Cross-multiplying gives:
4(T+2.5)=9T
Expanding the left side:
4T+10=9T
Rearranging gives:
10=9T−4T
Thus:
10=5T
Dividing both sides by 5:
T=2 N
The initial tension in the string is T=2 N.
Topper's Solved these Questions
- SUPERPOSITION OF WAVESBook:DC PANDEY ENGLISHChapter:SUPERPOSITION OF WAVESExercise:Level 2 More Than One Correct
Explore 6 Videos
- SUPERPOSITION OF WAVESBook:DC PANDEY ENGLISHChapter:SUPERPOSITION OF WAVESExercise:More than One correct Options
Explore 1 Video
- SUPERPOSITION OF WAVESBook:DC PANDEY ENGLISHChapter:SUPERPOSITION OF WAVESExercise:Subjective Questions
Explore 6 Videos
- SOUND WAVESBook:DC PANDEY ENGLISHChapter:SOUND WAVESExercise:Exercise 19.7
Explore 4 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBook:DC PANDEY ENGLISHChapter:THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESExercise:Medical entrance gallary
Explore 30 Videos
Similar Questions
Knowledge Check
In the question number 66, the tension in the string is
A30NB36NC34ND32NForce of friction and tension in a string are
AGravitational forcesBElectromagnetic forcesCNuclear forcesDWeal forces
The frequency of a stetched unifrom wire under tension is in resonance with the fundamental frequency of closed tube. If the tension in the wire is increased by 8 N, it is in resonance with the first overtone of the closed tube. The initial tension in the wire is
View SolutionIf the tension in a string is increased by 21 percent, the fundamental frequency of the string changes by 15Hz. Which of the following statements will also be correct?
View SolutionA piano note is compared to a tuning fork vibrating at 440 Hz. Three beats per second are listened by the piano tuner. When the tension in the string is increased slightly, the beat frequency increases. What was the initial frequency of the piano wire ?
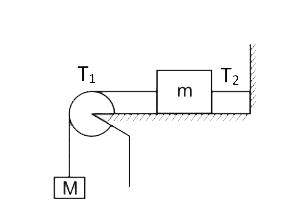
View SolutionFor the system shown in figure, the tensions in the string
View SolutionA wire of length one metre under a certain initial tension emits a sound of fundamental frequency 256 Hz. When the tesnion is increased by 1 kg wt , the frequency of the fundamental node increases to 320 Hz. The initial tension is
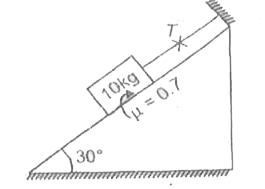
View SolutionThe tension T in the string shown in figure is
View Solution

