Question

In the question number 66, the tension in the string is

Options

A. 30N
B. 36N
C. 34N
D. 32N

Answer

C

Explanation

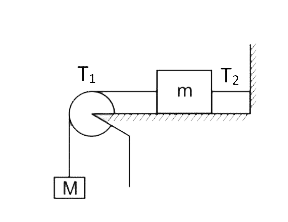
To solve the problem of finding the tension in the string, we can follow these steps:

Step 1: Understand the System
We have a block and a trolley system where the block is hanging and connected to the trolley via a string. We need to find the tension in the string.

Step 2: Identify Given Values
From the transcript, we have:
- The acceleration \( a = 1.5 \, \text{m/s}^2 \)
- The gravitational acceleration \( g = 10 \, \text{m/s}^2 \)
- The mass of the block \( m = 4 \, \text{kg} \) (since \( 4g \) is mentioned)

Step 3: Write the Equation of Motion
For the block hanging, we can write the equation of motion as:
\( 4g - T = 4a \)
Where:
- \( T \) is the tension in the string.
- \( 4g \) is the weight of the block.

Step 4: Substitute Known Values
Substituting the known values into the equation:
\( 4(10) - T = 4(1.5) \)
This simplifies to:
\( 40 - T = 6 \)

Step 5: Solve for Tension
Now, we can solve for \( T \):
\( 40 - 6 = T \)
\( T = 34 \, \text{N} \)

Conclusion
The tension in the string is \( 34 \, \text{N} \).