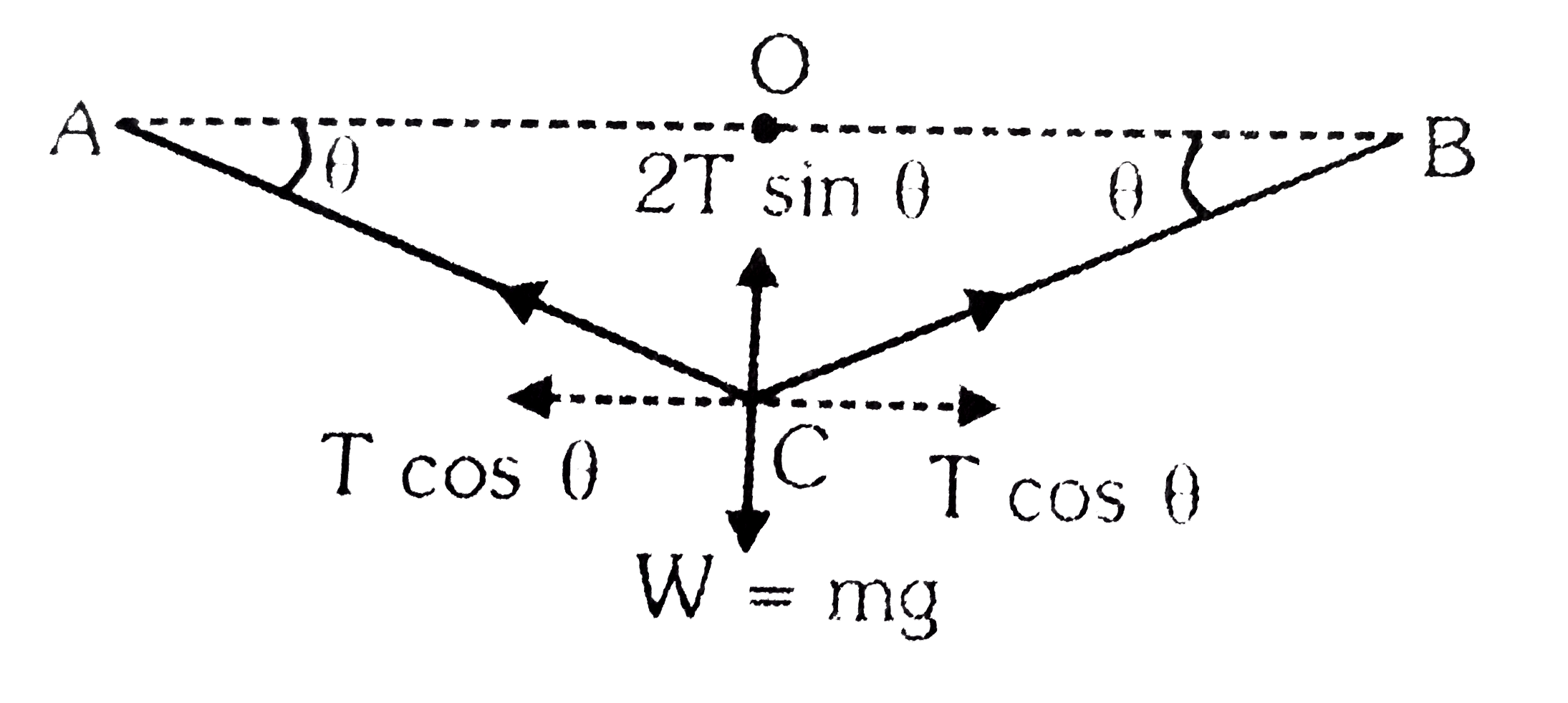
A bird with mass m parches at the middle of a strectched string Show that the tension in the string is give by T=mg2sinθ. Assuming that each half of the string is straight.

Initial position of wire=AOB, Final position of wire=ACB Let θ be the angle made by wire with horizontal, which is very small. Resolving tesntion T of string in horizontal and vertical direction, we note that the horizontal components cancel while vertical componets add and balance the weight. For equilibrium 2Tsinθ=W=mg⇒=W2sinθ
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - SWOE
44 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I
52 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
Similar Questions
The block of mass m is at rest. Find the tension in the string A .

View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.

View SolutionA 5.5 m length of string has a mass of 0.035 kg. If the tension in the string is 77 N the speed of a wave on the string is
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View SolutionA string of 7 m length has a mass of 0.035 kg. If tension in the string is 60.5 N, then speed of a wave on the string is :
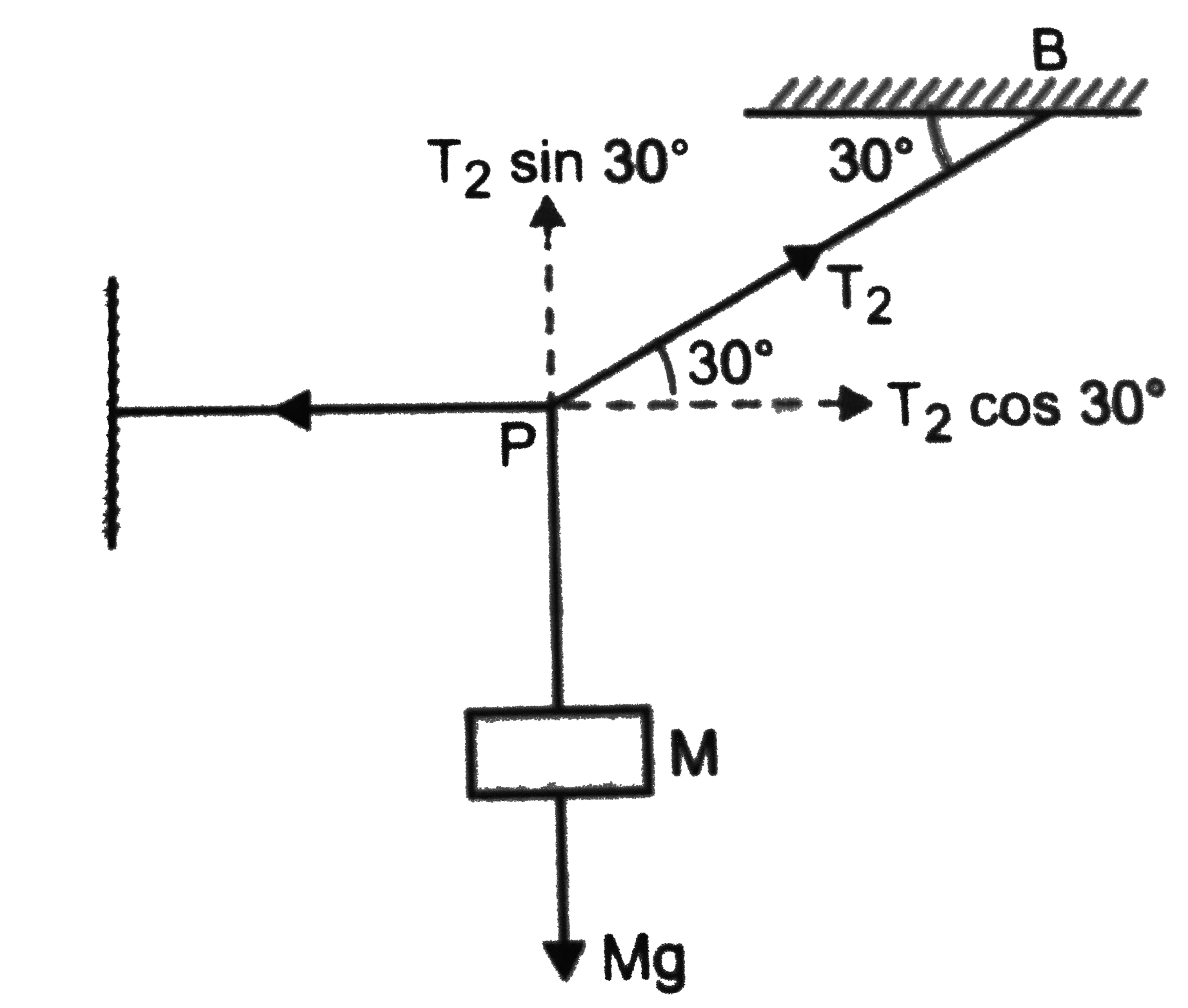
View SolutionA mass M is hung with a light inextensible string as shown in Find the tension in the horizontal part of the string .
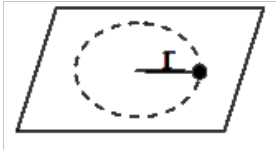
View SolutionA small mass attached to a string rotates on a frictionless table top as shown. If the tension in the string is increased by pulling the string causing the radius of the circular motion to decrease by a factor of 2, the kinetic energy of the mass will
View SolutionA string of mass per unit length μ is clamped at both ends such that one end of the string is at x=0 and the other is at x=L. When string vibrates in fundamental mode, amplitude of the midpoint of string is a and tension in the string is F. Find the total oscillation energy (in J) stored in the string. (Use L=1 m, F = 10N, a = 1/pi m).

View SolutionThe mass of the part of the string below A in figure is m. Find the tension of the string at the lower end and at A.
View SolutionA uniform rod of mass m and length l is suspended by means of two light inextensible strings as shown in figure. Tension in one string immediately after the other string is cut is

View Solution
