A man generates a symmetrical pulse in a string by moving his hand up and down. At the point in his hand moves downward. The pulse travels with speed of on the string & his hands passes times in each second from the mean position. Then the point on the string at a distance will reach its upper extreme first time at time
1.25 s
1s
23/24 s
The correct Answer is:C
To solve the problem step by step, we will analyze the motion of the pulse generated by the man's hand and determine when a point on the string at a distance of 3 meters will reach its upper extreme for the first time.
1. Understanding the Motion of the Hand:
- The man moves his hand up and down, crossing the mean position 6 times per second.
- Since he crosses the mean position twice in one complete cycle (once going up and once going down), the frequency f of the motion is:
f=6 crossings2=3 Hz
2. Calculating Angular Frequency (ω):
- The angular frequency ω is given by the formula:
ω=2πf
- Substituting the value of f:
ω=2π×3=6π radians/second
3. Calculating Wave Number (k):
- The wave travels with a speed v=3 m/s.
- The wave number k is calculated using the formula:
k=ωv
- Substituting the values of ω and v:
k=6π3=2π radians/meter
4. Using the Wave Equation:
- The wave equation can be expressed as:
y(x,t)=Asin(kx−ωt)
- For the upper extreme, y must equal the amplitude A. Thus, we set:
Asin(kx−ωt)=A
- This implies:
sin(kx−ωt)=1
- The sine function equals 1 at kx−ωt=π2+2nπ for any integer n. We will consider the first occurrence, so we set:
kx−ωt=π2
5. Substituting Values:
- For x=3 m:
k⋅3−ωt=π2
- Substituting k=2π and ω=6π:
2π⋅3−6πt=π2
- Simplifying:
6π−6πt=π2
6. Solving for t:
- Rearranging gives:
6π−π2=6πt
- Converting 6π to a fraction:
6π=12π2
- Thus:
12π2−π2=6πt
11π2=6πt
- Dividing both sides by 6π:
t=1112 seconds
Final Answer:
The point on the string at a distance of 3 meters will reach its upper extreme for the first time at time t=1112 seconds.
- The man moves his hand up and down, crossing the mean position 6 times per second.
- Since he crosses the mean position twice in one complete cycle (once going up and once going down), the frequency f of the motion is:
f=6 crossings2=3 Hz
- The angular frequency ω is given by the formula:
ω=2πf
- Substituting the value of f:
ω=2π×3=6π radians/second
- The wave travels with a speed v=3 m/s.
- The wave number k is calculated using the formula:
k=ωv
- Substituting the values of ω and v:
k=6π3=2π radians/meter
- The wave equation can be expressed as:
y(x,t)=Asin(kx−ωt)
- For the upper extreme, y must equal the amplitude A. Thus, we set:
Asin(kx−ωt)=A
- This implies:
sin(kx−ωt)=1
- The sine function equals 1 at kx−ωt=π2+2nπ for any integer n. We will consider the first occurrence, so we set:
kx−ωt=π2
- For x=3 m:
k⋅3−ωt=π2
- Substituting k=2π and ω=6π:
2π⋅3−6πt=π2
- Simplifying:
6π−6πt=π2
- Rearranging gives:
6π−π2=6πt
- Converting 6π to a fraction:
6π=12π2
- Thus:
12π2−π2=6πt
11π2=6πt
- Dividing both sides by 6π:
t=1112 seconds
The point on the string at a distance of 3 meters will reach its upper extreme for the first time at time t=1112 seconds.
Topper's Solved these Questions
- SUPERPOSITION OF WAVESBook:DC PANDEY ENGLISHChapter:SUPERPOSITION OF WAVESExercise:Level 2 More Than One Correct
Explore 6 Videos
- SUPERPOSITION OF WAVESBook:DC PANDEY ENGLISHChapter:SUPERPOSITION OF WAVESExercise:More than One correct Options
Explore 1 Video
- SUPERPOSITION OF WAVESBook:DC PANDEY ENGLISHChapter:SUPERPOSITION OF WAVESExercise:Subjective Questions
Explore 6 Videos
- SOUND WAVESBook:DC PANDEY ENGLISHChapter:SOUND WAVESExercise:Exercise 19.7
Explore 4 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBook:DC PANDEY ENGLISHChapter:THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESExercise:Medical entrance gallary
Explore 30 Videos
Similar Questions
Figure shows a wave pulse at t=0. The pulse moves to the right with a speed of 10cms^-1. Sketch the shape of the string at t=1s, 2s and 3s.

View SolutionA man travels half time of its journey with speed of 5m/s and for remaining half time he moves half of its total distance travelled, with speed of 3 m/s and remaining half distance with speed of 6 m/s. Find out the average speed of the man?
View SolutionThe equation of a wave pulse moving with a speed 1 m/sec at time t = 0 is given as y=f(x)=11+x2. Its equation at time t = 1 second can be given as
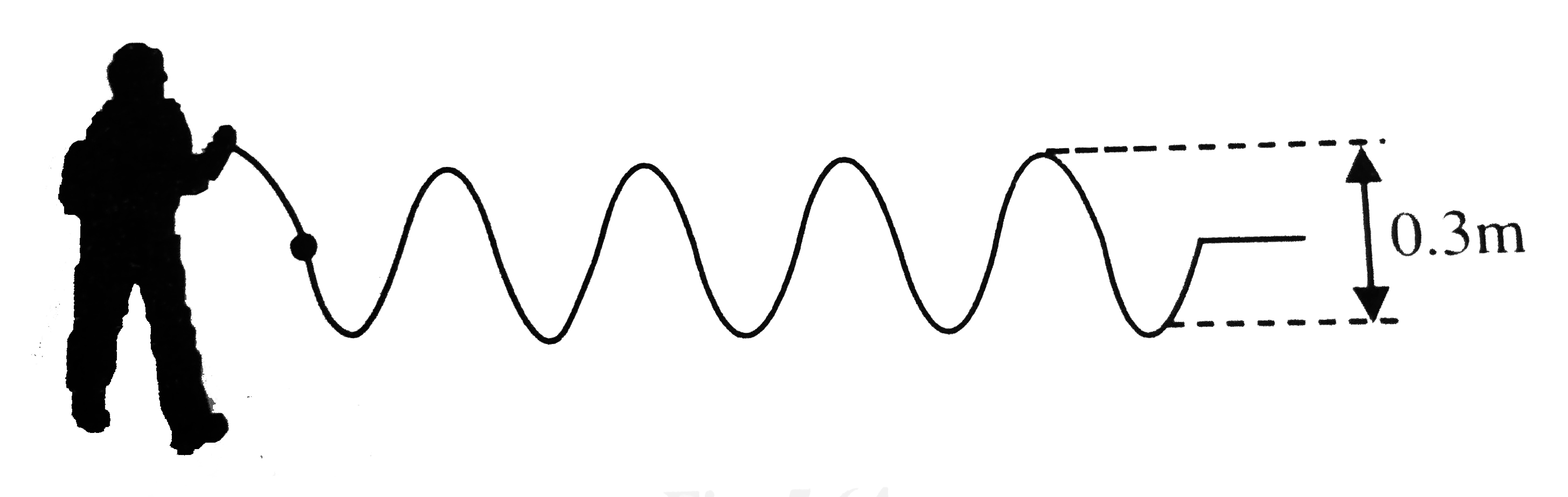
View Solutionfigure. Shows a student setting up wave wave on a long stretched string. The student's hand makes one complete up and down movement in 0.4s and in each up and down movement the hand moves by a height of 0.3m. The wavelength of the waves on the string is 0.8m.

The wave speed is
View SolutionA wave pulse on a string on a string has the dimension shown in figure. The wave speed is v=1 cm /s . If point O is a free end. The shape of wave at time t = 3s si

View SolutionA string of linear mass density 0.5gcm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end. The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20cms−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string ?

View SolutionA person moves towards East for 3 m, then towards North for 4 m and then moves vertically up by 5 m. What is his distance now from the starting point ?
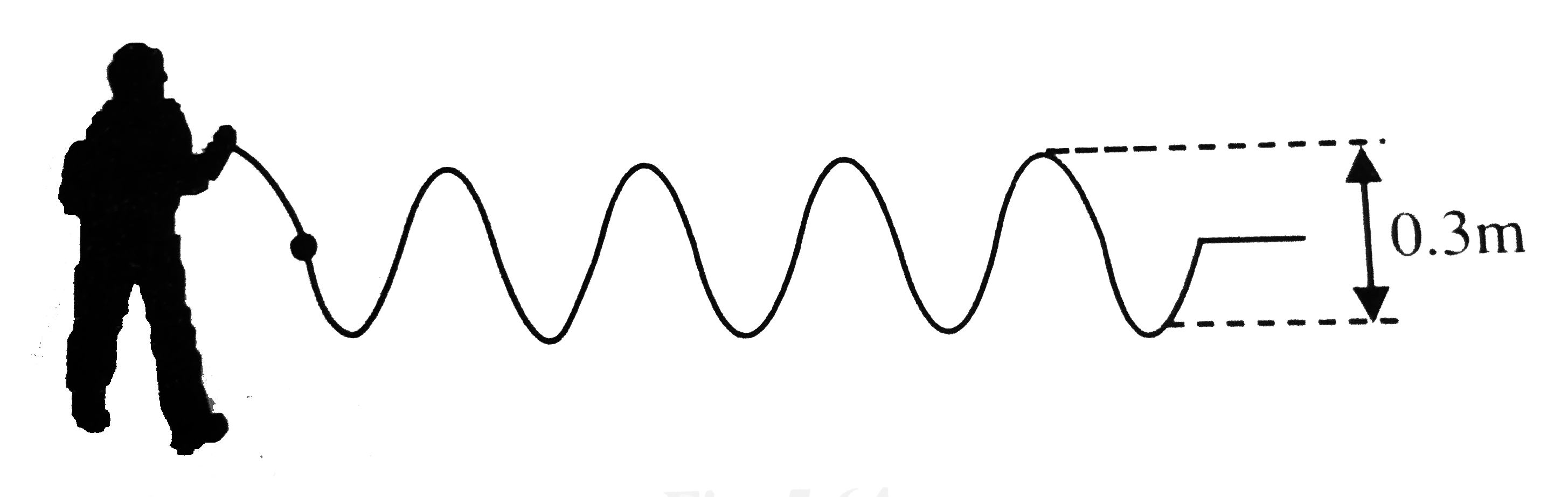
View Solutionfigure. Shows a student setting up wave wave on a long stretched string. The student's hand makes one complete up and down movement in 0.4s and in each up and down movement the hand moves by a height of 0.3m. The wavelength of the waves on the string is 0.8m.
The amplitude of the wave is
View Solutionfigure. Shows a student setting up wave wave on a long stretched string. The student's hand makes one complete up and down movement in 0.4s and in each up and down movement the hand moves by a height of 0.3m. The wavelength of the waves on the string is 0.8m.
The frequency of the wave is
View SolutionA rope is attached at one end to a fixed vertical pole . It is stretched horizontal with a fixed value of tension T . Suppose at t=0, a pulse is generated by moving the free end of the rope up and down once with your hand. The pulse arrives at the pole at instant t.
Ignoring the effect of gravity, answer the following quetions.
A.. If you move your hand up and down once but to a greater distance and in the same amount of time.
View Solution