One end of each of two identical springs, each of force constant 0.5N/m are attached on the opposite sides the a wooden block of mass 0.01kg. The other ends of the spring are connected to separate rigid supports such that the springs are unstrtched and are collinear in a horizontal plane. To the wooden piece is fixed a pointer which touches a vertically moving plane paper. The wooden piece kept on a smooth horizontal table is now displaced by 0.02m along the line of springs and released. If the speed of paper is 0.1m/s, find the equation of the path traced by the pointer on the paper and the distance between two consecutive maximum on this path. 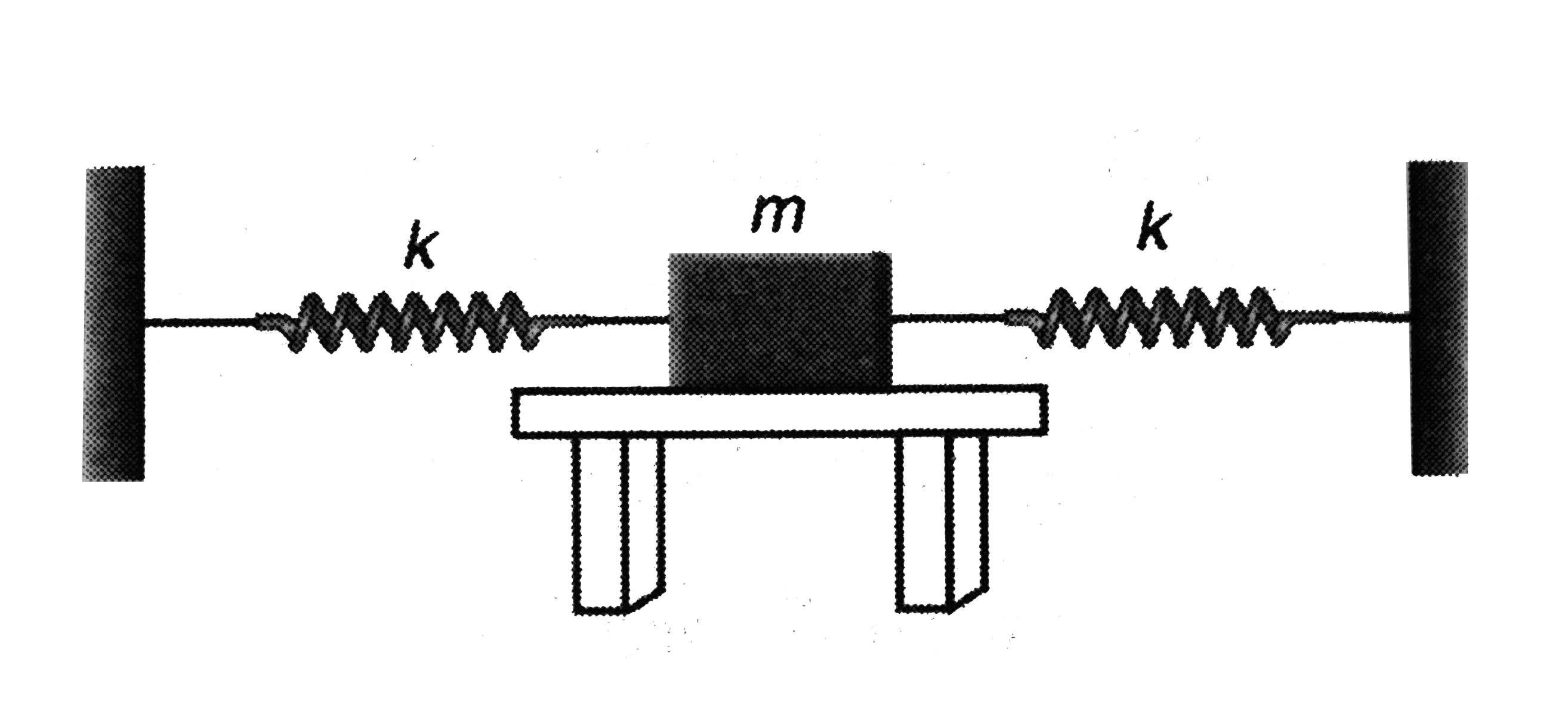
The correct Answer is:A, B, C
keff=2k=1.0N/m
f=12π√keffm=102πs−1
v=0.1ms,A=0.02m
λ=vf=0.1(102π)=2π100m
y=Acos(2πλ)(vt−x)
=0.02cos100(0.1t−x)
=0.02cos(10t−100x)m
The distance between two successive maxima
=λ=2π100=0.0628m
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Subjective Questions
2 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE MAINS
50 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Level 2 More Than One Correct
6 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
Knowledge Check
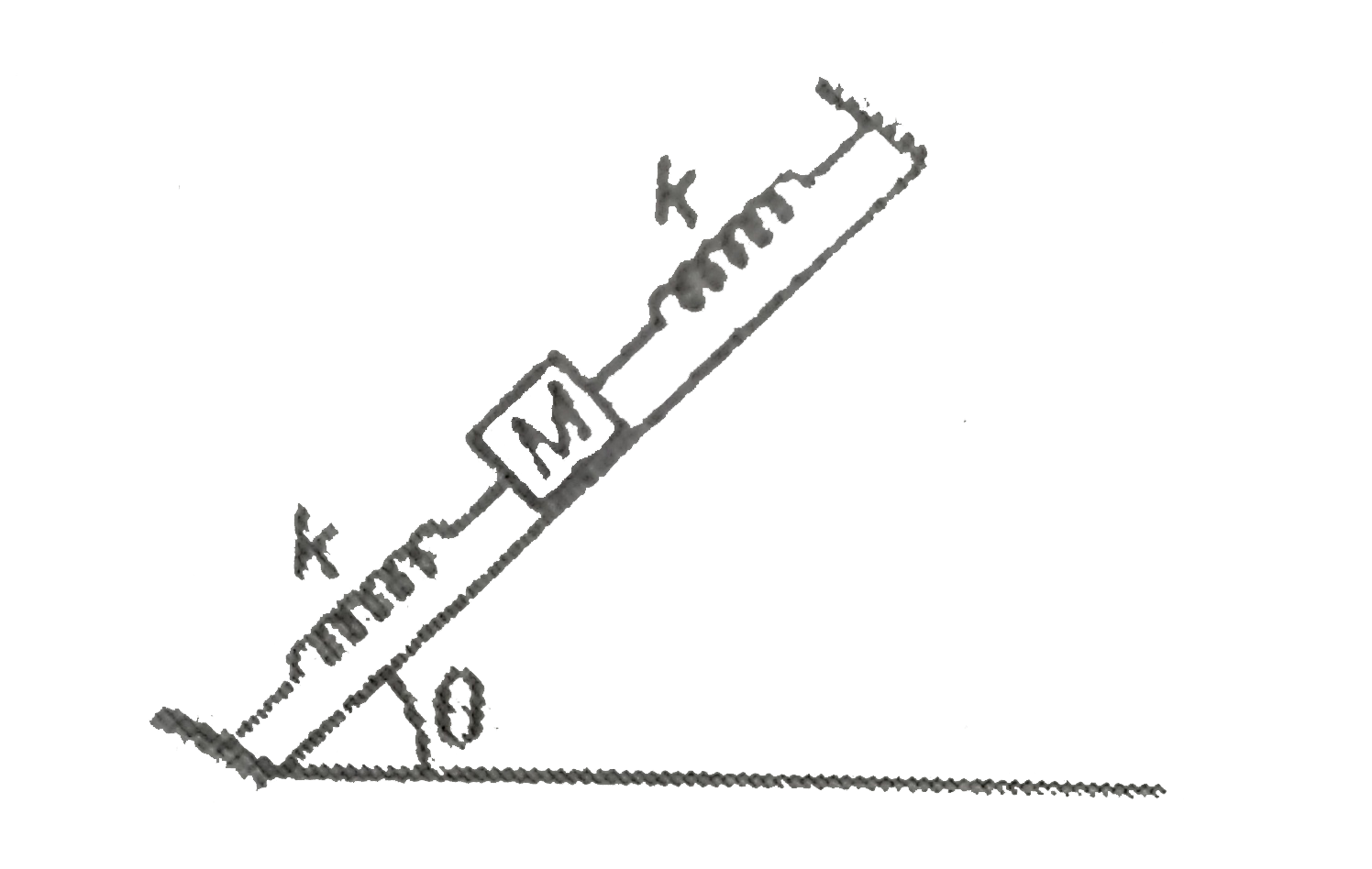
On a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is
 A1. 2π√M2kB2. 2π√2MkC3. 2π√Mgsinθ2kD4. 2π√2Mgk
A1. 2π√M2kB2. 2π√2MkC3. 2π√Mgsinθ2kD4. 2π√2Mgk
On a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
View SolutionTow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View SolutionA mass of 0.2 kg is attached to the lower end of a massless spring of force constant 200Nm the other end of which is fixed to a rigid support. Study the following statements.
View SolutionTwo blocks of masses 6 kg and 3 kg are attached to the two ends of a massless spring of spring constant 2π2N/m. If spring is compressed and released on a smooth horizontal surface then find the time period (in seconds) of each block.
View Solutiontwo light identical springs of spring constant K are attached horizontally at the two ends of a uniform horizontal rod AB of length l and mass m. the rod is pivoted at its centre 'o' and can rotate freely in horizontal plane . The other ends of the two springs are fixed to rigid supportss as shown in figure . the rod is gently pushed through a small angle and released , the frequency of resulting oscillation is :
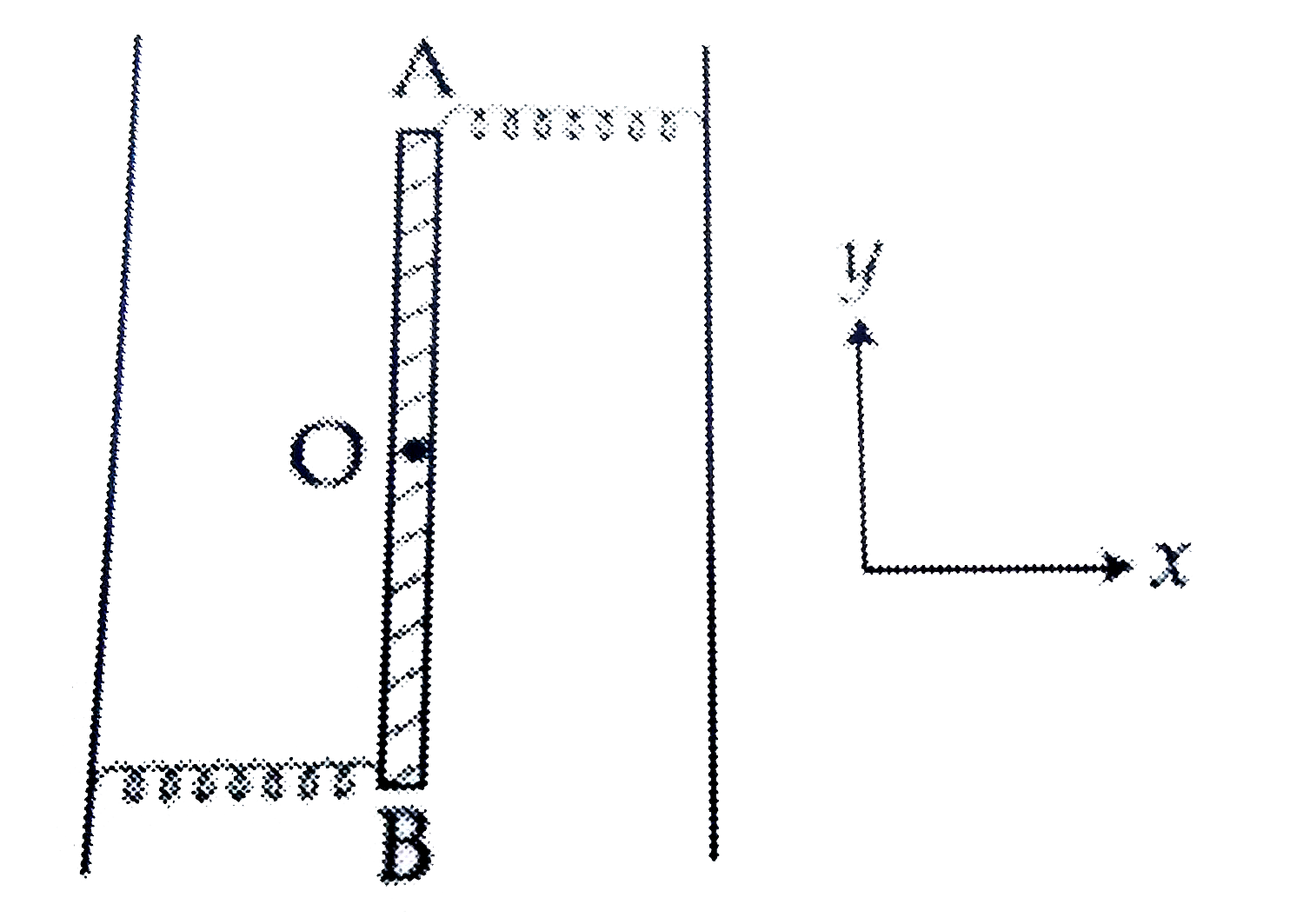
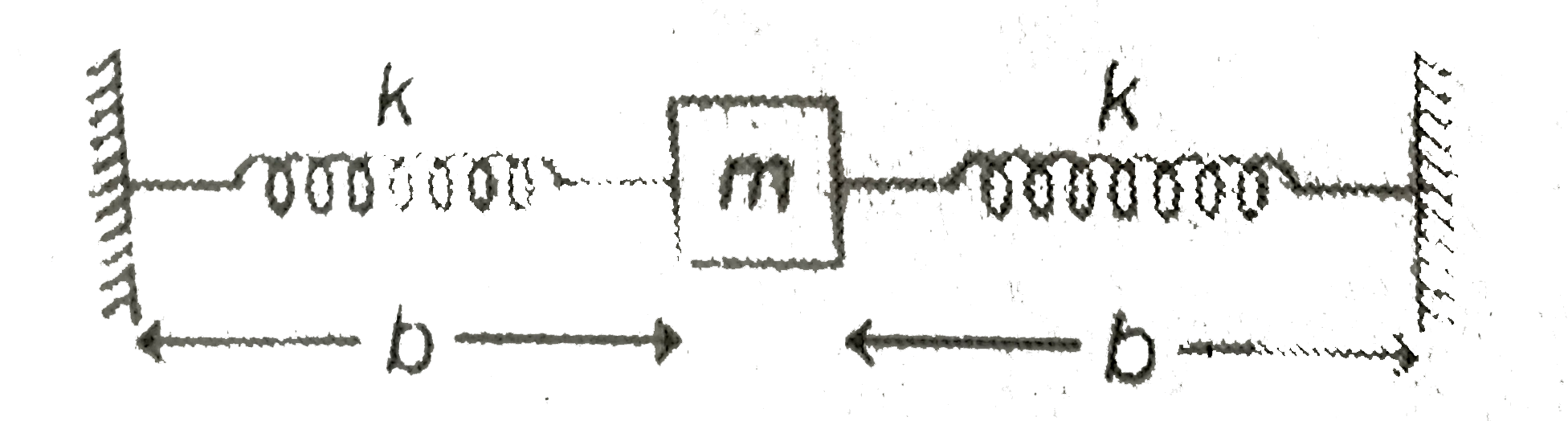
View SolutionIn the figure, a block of mass m is rigidly attached to two identical springs of stiffness k each. The other ends of the springs are connected to the fixed wall. When the block is in equilibrium, length of each spring is b, which is greater than the natural length of the spring. The time period of the oscillation of the block if it is displaced by small distance perpendicular to the length of the springs and released. Space is gravity free.
View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance x0 from the block. The spring is then compressed by 2x0 and released. The time taken to strike the wall is

View Solution

