A sinusoidal transverse wave travel on a string. The string has length 8.00m and mass 6.00g. The wave speed is 30.0m/s and the wavelength is 0.200m. (a) If the wave is to have an average power of 50.0W, what must be the amplitude of the wave? (b) For the same string, if the ampitude and wavelength are the same as in part (a) what is the average power for the wave if the tension is increased such that the wave speed is doubled?
The correct Answer is:A, B, C, D
To solve the problem step by step, we will break it down into parts (a) and (b) as given in the question.
Part (a): Finding the Amplitude
1. Given Data:
- Length of the string, L=8.00m
- Mass of the string, m=6.00g=0.006kg
- Wave speed, v=30.0m/s
- Wavelength, λ=0.200m
- Average power, P=50.0W
2. Calculate the Linear Mass Density (μ):
μ=mL=0.006kg8.00m=0.00075kg/m
3. Calculate the Wave Number (k):
k=2πλ=2π0.200m=10πrad/m
4. Calculate the Angular Frequency (ω):
Using the relationship v=ωk:
ω=v⋅k=30.0m/s⋅10πrad/m=300πrad/s
5. Power Formula:
The average power for a sinusoidal wave on a string is given by:
P=12μω2A2
Rearranging for amplitude A:
A2=2Pμω2
6. Substitute the Values:
A2=2⋅50.0W0.00075kg/m⋅(300πrad/s)2
A2=100.00.00075⋅90000π2
A2=100.00.00075⋅282743.34≈100.0212.0575≈0.471
A≈√0.471≈0.686m≈68.6cm
Part (b): Average Power with Increased Wave Speed
1. New Wave Speed:
The wave speed is doubled:
v′=2v=2⋅30.0m/s=60.0m/s
2. New Angular Frequency:
Using the new wave speed:
ω′=v′⋅k=60.0m/s⋅10πrad/m=600πrad/s
3. New Power Formula:
The average power can be recalculated using the same amplitude A and the new angular frequency:
P′=12μω′2A2
Since ω′=2ω:
P′=12μ(2ω)2A2=4⋅12μω2A2=4P
P′=4⋅50.0W=200.0W
Final Answers:
(a) The amplitude of the wave is approximately 68.6cm.
(b) The average power for the wave with doubled wave speed is 200.0W.
- Length of the string, L=8.00m
- Mass of the string, m=6.00g=0.006kg
- Wave speed, v=30.0m/s
- Wavelength, λ=0.200m
- Average power, P=50.0W
μ=mL=0.006kg8.00m=0.00075kg/m
k=2πλ=2π0.200m=10πrad/m
Using the relationship v=ωk:
ω=v⋅k=30.0m/s⋅10πrad/m=300πrad/s
The average power for a sinusoidal wave on a string is given by:
P=12μω2A2
Rearranging for amplitude A:
A2=2Pμω2
A2=2⋅50.0W0.00075kg/m⋅(300πrad/s)2
A2=100.00.00075⋅90000π2
A2=100.00.00075⋅282743.34≈100.0212.0575≈0.471
A≈√0.471≈0.686m≈68.6cm
The wave speed is doubled:
v′=2v=2⋅30.0m/s=60.0m/s
Using the new wave speed:
ω′=v′⋅k=60.0m/s⋅10πrad/m=600πrad/s
The average power can be recalculated using the same amplitude A and the new angular frequency:
P′=12μω′2A2
Since ω′=2ω:
P′=12μ(2ω)2A2=4⋅12μω2A2=4P
P′=4⋅50.0W=200.0W
(a) The amplitude of the wave is approximately 68.6cm.
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Subjective Questions
2 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE MAINS
50 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Level 2 More Than One Correct
6 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
Knowledge Check
The speed of transverse wave on a stretched string is
Adirectly proportional to the tension in the stringBdirectly proportional to the square root of the tensionCinversely proportional to liveDinversely proportional to sqyare of tension
A transverse wave is propagating on a stretched string of mass per unit length32gm−1. The tension on the string is 80 N. The speed of the wave over the string is
View SolutionTransverse waves travel with a speed of 20.0m/sin a string under a tension of 6.00 N. what tension is requared for a wave speed of 30.0m/s in the same string?
View SolutionA transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is [
View SolutionA string fixed at both ends is 8.40m long and has a mass of 0.120kg. It is subjected to a tension of 96.0N and set oscillating. (a) What is the speed of the waves on the string? (b) What is the longest possible wavelength for a standing wave ? (c) Give the frequency of the wave.
View Solutionfigure. Shows a student setting up wave wave on a long stretched string. The student's hand makes one complete up and down movement in 0.4s and in each up and down movement the hand moves by a height of 0.3m. The wavelength of the waves on the string is 0.8m.
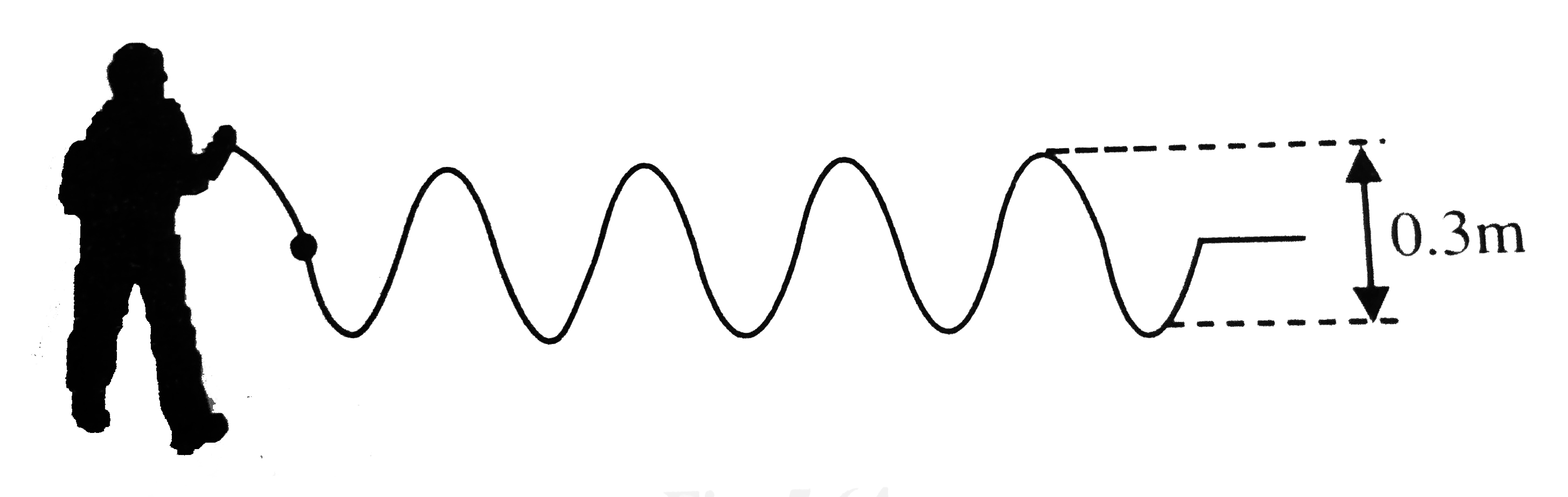
The amplitude of the wave is
View SolutionA piano wire with mass 3.00 g and length 80.0 cm is stretched with a tension of 25.0 N. A wave with frequancy 120.0 Hz and amplitude 1.6 mm travels along the wire. (a) calculate the average power carried by the wave. (b) what happenes to the avarage power if the wave amplitude is halved?
View SolutionA sinusoidal wave is propagating along a streched string that lies along the x-axis. The displacement of the string as a function of time is graphed in for particles at x-0 and at x=0.0900 m. (a) what is the amplitude of the wave? (b)what is the period of the wave? (c ) you are told that the two points x=0 and x=0.0900 m are within one wavelength of each other. if the wave is moving in the +x-direction, determine the wavelength and the wave speed. (d) if instead the wave is moving in the -x-direction, determine the wavelength and the wave speed. (e) would it be possible to derermine definitely the wavelength in parts (c ) and (d) if you were not told that the two points were within one wavelength of each other? why ot why not?
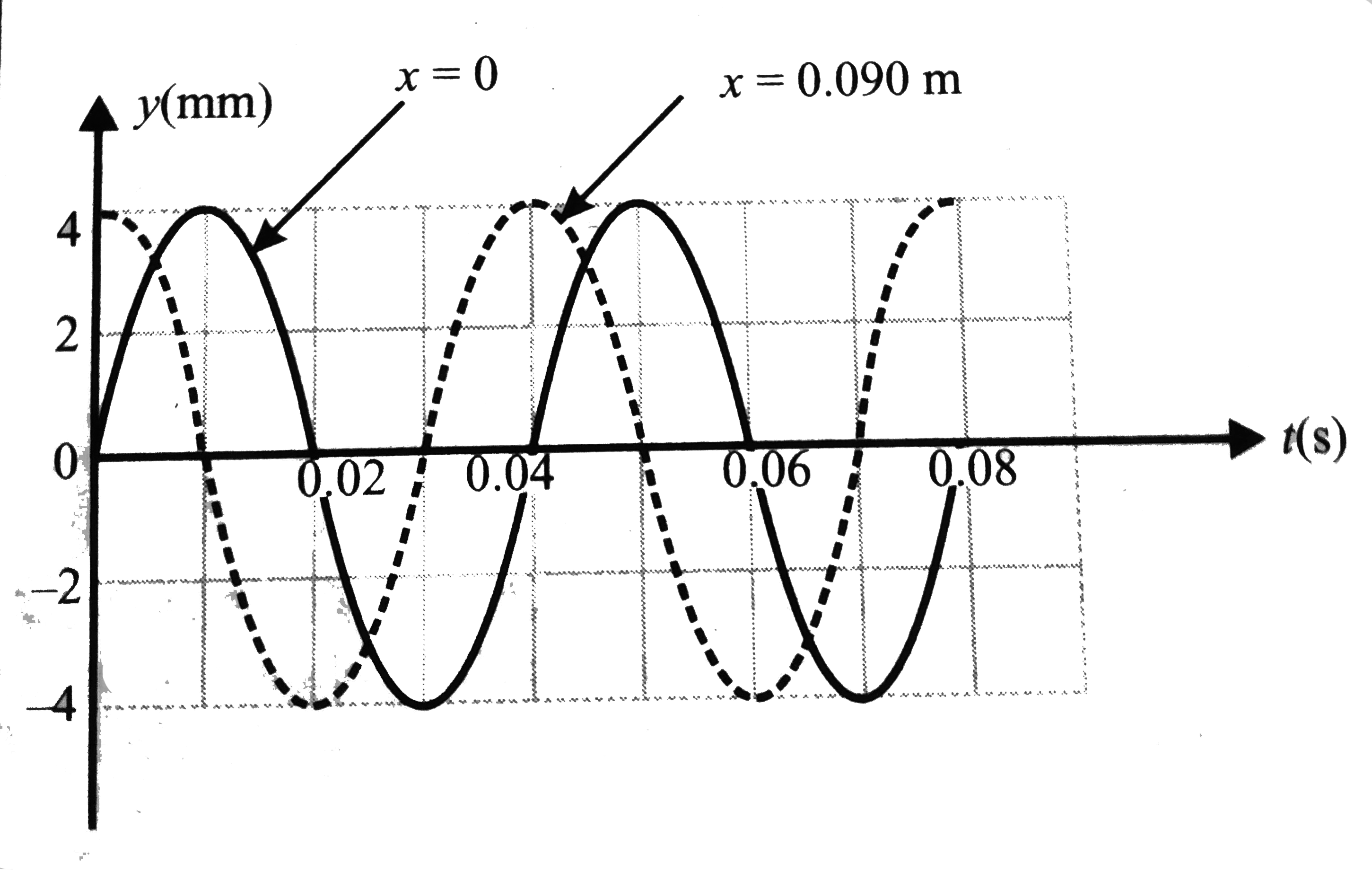
View Solution

