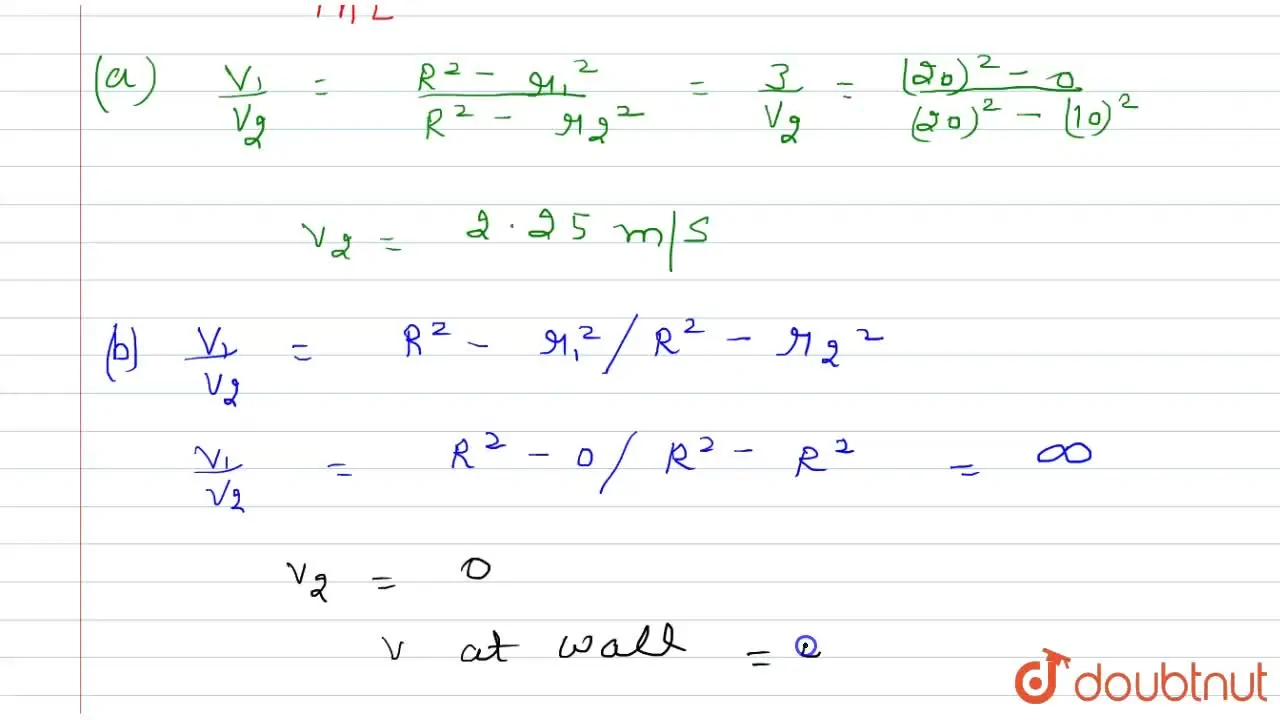Water at 20∘ is flowing in a pipe of radius 20.0cm . The viscosity of water at 20∘C is 1.005 centipise. If the water's speed in the centre of the pipe is 3.00m/s, what is water's speed:
(a) 10.0cm from the centre of the pipe(half way between the centre and the walls)
(b) at the wall of the pipe?
The correct Answer is:A, B
v=p1−p24ηL(R2−r2)
or, v∝R2−r2
(a) v1v2=R2−r21R2−r22
or, 3v2=400−0400−100
∴v2=2.25m/s
(b)v2=(R2−r21R2−r21)v1
v2=0at r2=R.
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question2videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Single Correct36videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 1 Single Correct49videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
Water flows at a speed 5 cm s−1 through a pipe of radius 2 cm. The visosity of water is 0.001 PI. The Reynolds number and the nature of flow are respectively
View Solution|f. water is flowing in a pipe with speed 2 m/s then its kinetic energy per unit volume is
View SolutionWater at 20∘C is flowing in a horizontal pipe that is 20.0m long.The flow is laminar and the water completely fills the pipe. A pump maintains a gauge pressure of 1400Pa, at a large tank at one end of the pipe. The other end of the pipe is open to the air, The viscosity of water at 20∘C is 1.005 poise
(a) If the pipe has diameter 8.0cm, what is the volume flow rate?
(b) What gauge pressure must the pump provide to achieve the same volume flow rate for a pipe with a diameter of 4.0cm?
(c) For pipe in part (a) and the same gauge pressure maintained by the pump, what does the volume flow rate become if the water is at a temperature of 60∘C (the viscosity of water at 60∘C is 0.469 poise?View SolutionA gardener waters the plants by a pipe of diameter 1 cm . The water comes out at the rate of 20 cc/s . The reactionary force exerted on the hand of the gardener is
View SolutionWater is flowing in a pipe of radius 1.5 cm with an average velocity 15 cm s−1. What is the nature of flow? Given coefficient of viscosity of water is 10−3 kg m−1s−1 and its density is 103 kg m−3
View SolutionOne end of a cylinderical pipe has a radius of 2 cm. Water comes out at 10 m/s. The rate at which mass is leaving the pipe is
View SolutionWater flows through a horizontal pipe of radius 1 cm at a speed of 8 cm s−1. What will be the speed of flow of water under similar conditions, if the radius of the pipe is doubled ?
View SolutionA hose-pipe of cross-section area 2cm2 delivers 1500 litres of water in 5 minutes. What is the speed of water in m/s through the pipe?
View SolutionIt water flows horizontally through a pipe of varying cross section and the pressure of water equals 10cm of g at a point where the velocity of flow is 40cm/s, what is the pressure at another point where the velocity of flow is 50cm/s?
View SolutionWater flows at a speed of 6 cms−1 through a tube of radius 1 cm. coefficient of viscosity of water at room temperature is 0.01 poise. Calculate the Reynolds number. Is it a steady flow.
View Solution