For a two body oscillator system, prove the relation,
T=2π√μk
where, μ=m1m2m1+(m2)= reduced mass.
The correct Answer is:A
To prove the relation T=2π√μk for a two-body oscillator system, where μ=m1m2m1+m2 is the reduced mass, we will follow these steps:
Step 1: Understand the System
We have two masses m1 and m2 connected by a spring with spring constant k. When the system is displaced, both masses will experience forces due to the spring.
Step 2: Define the Displacement
Let x1 be the displacement of mass m1 and x2 be the displacement of mass m2. The total extension of the spring can be expressed as:
x=x1−x2−L0
where L0 is the natural length of the spring.
Step 3: Apply Newton's Second Law
According to Newton's second law, the force on each mass due to the spring can be expressed as:
F=−kx
For mass m1:
m1d2x1dt2=−k(x1−x2−L0)
For mass m2:
m2d2x2dt2=−k(x2−x1+L0)
Step 4: Combine the Equations
Rearranging the equations gives us two second-order differential equations. We can express the relative displacement x=x1−x2.
Step 5: Formulate the Differential Equation
By substituting x1 and x2 into the equations and eliminating one of the variables, we can derive a single equation in terms of x:
μd2xdt2=−kx
where μ=m1m2m1+m2 is the reduced mass.
Step 6: Identify the Form of the Equation
The equation μd2xdt2=−kx is a standard form of the simple harmonic motion equation, which can be written as:
d2xdt2+kμx=0
Step 7: Determine the Time Period
The general solution for the time period T of simple harmonic motion is given by:
T=2π√massspring constant
In our case, substituting μ for mass and k for spring constant gives:
T=2π√μk
Conclusion
Thus, we have proved that the time period T of a two-body oscillator system is given by:
T=2π√μk
---
We have two masses m1 and m2 connected by a spring with spring constant k. When the system is displaced, both masses will experience forces due to the spring.
Let x1 be the displacement of mass m1 and x2 be the displacement of mass m2. The total extension of the spring can be expressed as:
x=x1−x2−L0
where L0 is the natural length of the spring.
According to Newton's second law, the force on each mass due to the spring can be expressed as:
F=−kx
For mass m1:
m1d2x1dt2=−k(x1−x2−L0)
For mass m2:
m2d2x2dt2=−k(x2−x1+L0)
Rearranging the equations gives us two second-order differential equations. We can express the relative displacement x=x1−x2.
By substituting x1 and x2 into the equations and eliminating one of the variables, we can derive a single equation in terms of x:
μd2xdt2=−kx
where μ=m1m2m1+m2 is the reduced mass.
The equation μd2xdt2=−kx is a standard form of the simple harmonic motion equation, which can be written as:
d2xdt2+kμx=0
The general solution for the time period T of simple harmonic motion is given by:
T=2π√massspring constant
In our case, substituting μ for mass and k for spring constant gives:
T=2π√μk
Thus, we have proved that the time period T of a two-body oscillator system is given by:
T=2π√μk
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Assertion And Reason
Explore 10 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Single Correct
Explore 24 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Example Type 13
Explore 3 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
There are two blocks of masses m1 and m2,m1 is placed on m2 on a table which is rotating with an angular velocity ω about the vertical axis . The coefficent of friction between the block is μ1 and between m2 and table is μ2(μ1<μ2) if block are placed at distance R from the axis of ratation , for relative sliding between the surface in contact , find the
a. friction force at the contacting surface
b. maximum angular speed ω

View SolutionFigure shows two shells of masses m1 and m2 . The shells are concentric. At which point, a particle of mass m shall experience zero force?
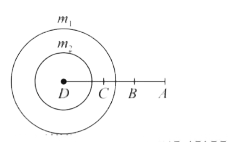
View SolutionFigure shows two shells of masses m1 and m2 . The shells are concentric. At which point, a particle of mass m shall experience zero force?
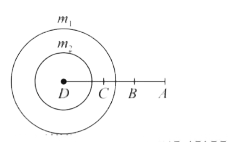
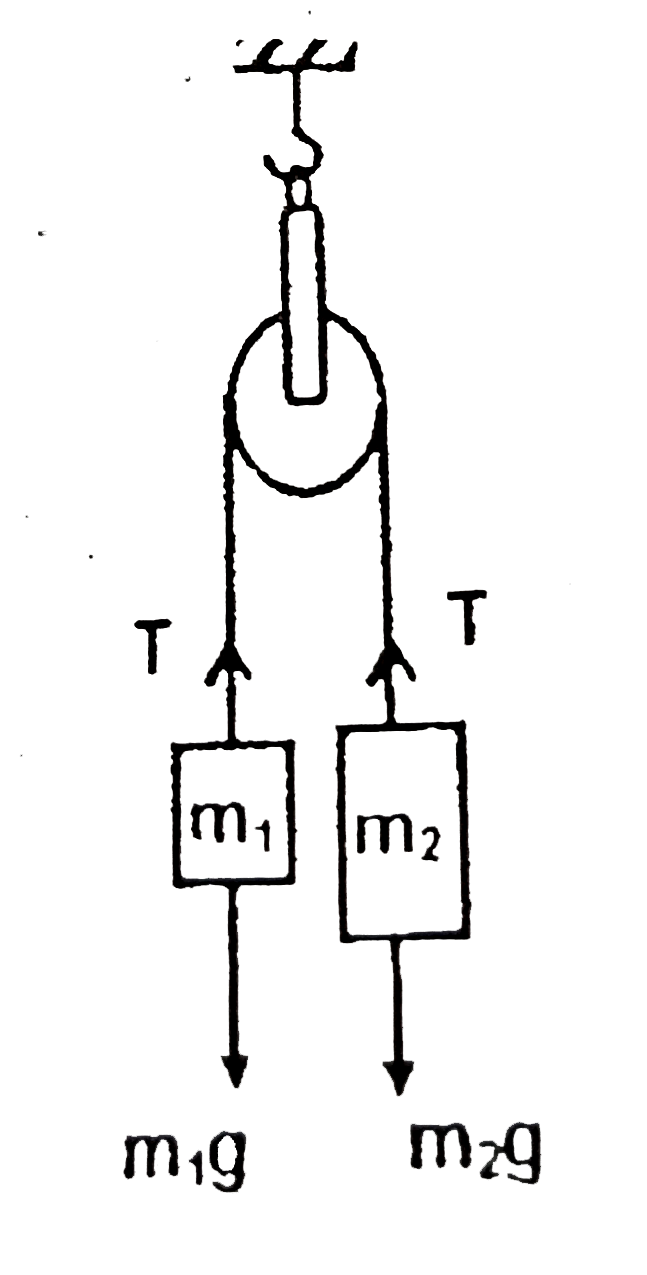
View SolutionConsider the case of two bodies of masses m1 and m2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations :
(i) when m1>m2. In this case
a=(m1−m2m1+m2)g and T=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)g and T=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0, T=mg
If m1=10kg, m2=6kg and g=10m/s2
If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string
View SolutionFor any prism, prove that .n. or μ=sin(A+δm2)sin(A2) where the terms have their usual meaning
View SolutionTwo bodies of masses m1 and m2 are placed distant d apart. Show that the position where the gravitational field due to them is zero, the potential is given by, V=−Gd(m1+m2+2√m1m2)
View SolutionTwo bodies of masses 1kg and 3kg are lying in xy plane at (0,0) and (2,−1) respectively. What are the coordinates of the centre of mass ?
Hint. xcm=m1x1+m2x2m1+x2, ycm=m1y1+m2y2m1+m2
View SolutionTwo stars of mass M1&M2 are in circular orbits around their centre of mass The star of mass M1 has an orbit of radius R1 the star of mass M2 has an orbit of radius R2 (assume that their centre of mass is not acceleration and distance between starts is fixed)
(a) Show that the ratio of orbital radii of the two stars equals the reciprocal of the ratio of their masses, that is R1/R2=M2/M1
(b) Explain why the two stars have the same orbital period and show that the period
T=2π(R1+R2)3/2√G(M1+M2) .
View SolutionThe p−V diagram of two different masses m1 and m2 are drawn (as shown) at constant temperature (T). State whether m1>m2orm2>m2.
 .
.
View SolutionTwo particles of masses m1andm2 are joined by a light rigid rod of length r. The system rotates at an angular speed ω about an axis through the centre of mass of the system and perpendicular to the rod. Show that the angular momentum of the system is L=μr2ω where μ is the reduced mass of the system defined as μ=m1m2m1+m2
View Solution

