Two particles move parallel to x−axis about the origin with same amplitude 'a' and frequency ω. At a certain instant they are found at a distance a/3 from the origin on opposite sides but their velocities are in the same direction. What is the phase difference between the two?
The correct Answer is:A, C
To solve the problem, we need to find the phase difference between two particles moving in simple harmonic motion (SHM) given their positions and velocities. Let's break down the solution step by step.
Step 1: Understanding the Problem
We have two particles, P1 and P2, moving along the x-axis. They have the same amplitude a and frequency ω. At a certain instant, P1 is at position a3 and P2 is at position −a3. Both particles have velocities in the same direction.
Step 2: Write the Equations of Motion
The position of the first particle (P1) can be described by:
x1=asin(ωt)
For the second particle (P2), we can express its position with a phase difference ϕ:
x2=asin(ωt+ϕ)
Step 3: Substitute the Given Positions
From the problem, we know:
x1=a3andx2=−a3
Substituting these into the equations gives us:
a3=asin(ωt)⇒sin(ωt)=13
−a3=asin(ωt+ϕ)⇒sin(ωt+ϕ)=−13
Step 4: Use the Sine Addition Formula
Using the sine addition formula for sin(ωt+ϕ):
sin(ωt+ϕ)=sin(ωt)cos(ϕ)+cos(ωt)sin(ϕ)
Substituting sin(ωt)=13:
−13=13cos(ϕ)+cos(ωt)sin(ϕ)
Step 5: Find cos(ωt)
To find cos(ωt), we can use the Pythagorean identity:
cos2(ωt)+sin2(ωt)=1
Substituting sin(ωt)=13:
cos2(ωt)+(13)2=1⇒cos2(ωt)+19=1
cos2(ωt)=1−19=89⇒cos(ωt)=±2√23
Step 6: Substitute Back to Find ϕ
Now substituting back into the equation:
−13=13cos(ϕ)+(±2√23)sin(ϕ)
Multiplying through by 3 to eliminate the fraction:
−1=cos(ϕ)±2√2sin(ϕ)
Step 7: Solve for ϕ
This gives us two equations depending on the sign of cos(ωt). We can solve these equations to find ϕ.
Assuming cos(ωt)=2√23:
−1=2√23cos(ϕ)+2√2sin(ϕ)
This is a trigonometric equation that can be solved for ϕ.
Final Result
After solving the equations, we find that the phase difference ϕ can be determined as:
ϕ=cos−1(79)orϕ=π−cos−1(79)
We have two particles, P1 and P2, moving along the x-axis. They have the same amplitude a and frequency ω. At a certain instant, P1 is at position a3 and P2 is at position −a3. Both particles have velocities in the same direction.
The position of the first particle (P1) can be described by:
x1=asin(ωt)
For the second particle (P2), we can express its position with a phase difference ϕ:
x2=asin(ωt+ϕ)
From the problem, we know:
x1=a3andx2=−a3
Substituting these into the equations gives us:
a3=asin(ωt)⇒sin(ωt)=13
−a3=asin(ωt+ϕ)⇒sin(ωt+ϕ)=−13
Using the sine addition formula for sin(ωt+ϕ):
sin(ωt+ϕ)=sin(ωt)cos(ϕ)+cos(ωt)sin(ϕ)
Substituting sin(ωt)=13:
−13=13cos(ϕ)+cos(ωt)sin(ϕ)
To find cos(ωt), we can use the Pythagorean identity:
cos2(ωt)+sin2(ωt)=1
Substituting sin(ωt)=13:
cos2(ωt)+(13)2=1⇒cos2(ωt)+19=1
cos2(ωt)=1−19=89⇒cos(ωt)=±2√23
Now substituting back into the equation:
−13=13cos(ϕ)+(±2√23)sin(ϕ)
Multiplying through by 3 to eliminate the fraction:
−1=cos(ϕ)±2√2sin(ϕ)
This gives us two equations depending on the sign of cos(ωt). We can solve these equations to find ϕ.
−1=2√23cos(ϕ)+2√2sin(ϕ)
This is a trigonometric equation that can be solved for ϕ.
After solving the equations, we find that the phase difference ϕ can be determined as:
ϕ=cos−1(79)orϕ=π−cos−1(79)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Assertion And Reason
Explore 10 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Single Correct
Explore 24 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Example Type 13
Explore 3 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
Two particles move parallel to x - axis about the origin with the same amplitude and frequency. At a certain instant they are found at distance A3 from the origin on opposite sides but their velocities are found to be in the same direction. What is the phase difference between the two ?
View SolutionTwo particles execute SHM of same amplitude and frequency on parallel lines. They pass one another when moving in opposite directions each time their displacement is half of their amplitude. What is the phase difference between them?
View Solution
Knowledge Check
Two particles execute SHM of same amplitude and frequency on parallel lines. They pass one another when moving in opposite directions each time their displacement is one third their amplitude. What is the phase difference between them?
A0B2π3CπDπ6Two particles execute SHMs of the same amplitude and frequency along the same straight line. They cross one another when going in opposite direction. What is the phase difference between them when their displacements are half of their amplitudes ?
A60∘B30∘C120∘D150∘
A particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
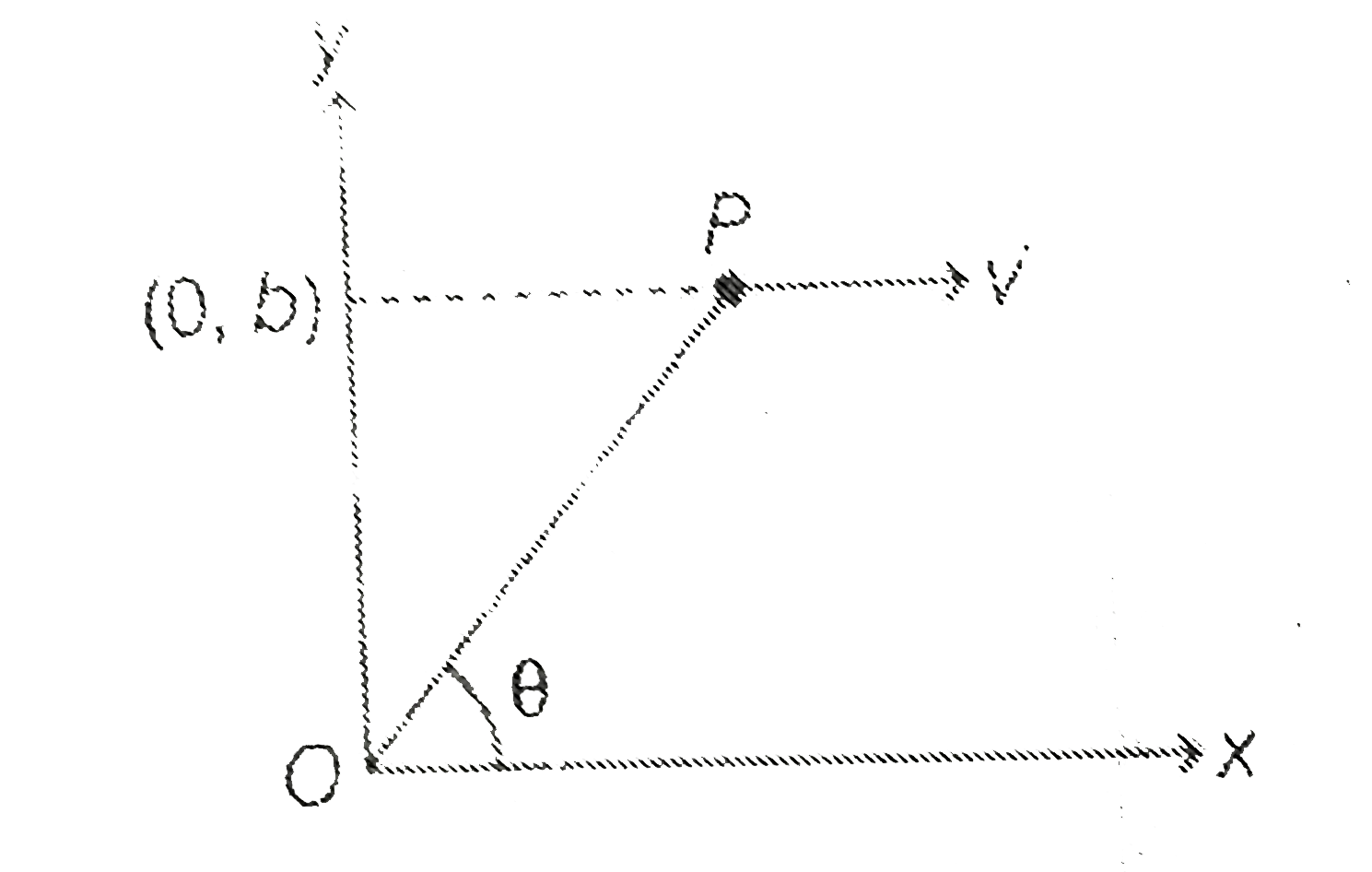
View SolutionTwo bodies performing S.H.M. have same amplitude and frequency. Their phases at a certain instant are as shown in the figure. The phase difference between them is
_E01_002_Q01.png)
View SolutionTwo particles execute simple harmonic motion of the same amplitude and frequency along close parallel lines. They pass each other moving in opposite directions each time their displacement is half their amplitude. Their phase difference is
View SolutionTwo particles are in SHM with the same amplitude and frequency along the same line and about the same point. If the maximum separation between them is √3 times their amplitude, the phase difference between them is 2πn. Find value of n
View SolutionTwo particles are executing simple harmonic of the same amplitude (A) and frequency ω along the x-axis . Their mean position is separated by distance Xo. (Xo>A). If the maximum separation between them is (Xo+A), the phase difference between their motion is:
View SolutionTwo particles are in SHM with same amplitude A and same regualr frequency ω. At time t=0, one is at x =+A2 and the other is at x=−A2. Both are moving in the same direction.
View Solution