A block of mass M slides along a horizontal table with speed v0. At x=0, it hits a spring with spring constant k and begins to experience a friction force. The coefficient of friction is variable and is given by μ=bx, where b is a positive constant. Find the loss in mechanical energy when the block has first come momentarily to rest.
 .
.
The correct Answer is:B
Net retarding force =kx+bMgx
∴ Net retardatopm =(k+bMgM).x
So, we can write
v.dvdx=−(k+bMtgM).x
v.dvdx=−(k+bMgM)∫x0xdx
or ∫0v0v.dv=−(k+bMgM)∫x0xdx
or x=√MkbMgv0
Loss in vechanical energy
ΔE=12Mv20−12kx2
or ΔE=12Mv20−12(mk+bMg)v20
or ΔE=v202[M−k(Mk+bMg)]
=v20M2g2(k+bMg).
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 More Than One Correct
9 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA block of mass m moving with a velocity v0 on a rough horizontal surface from x=0 coefficient of friction is given by μ=μ0+ax. Find the kinetic energy of the block as function of x before it comes to rest.
View SolutionA block of mass m slides 0n a frictionless table. It is constrained to move inside a ring of radius R . At time t=0 , block is moving along the inside of the ring (i.e. in the tangential direction) with velocity v0 . The coefficient of friction between the block and the ring is μ . Find the speed of the block at time t .

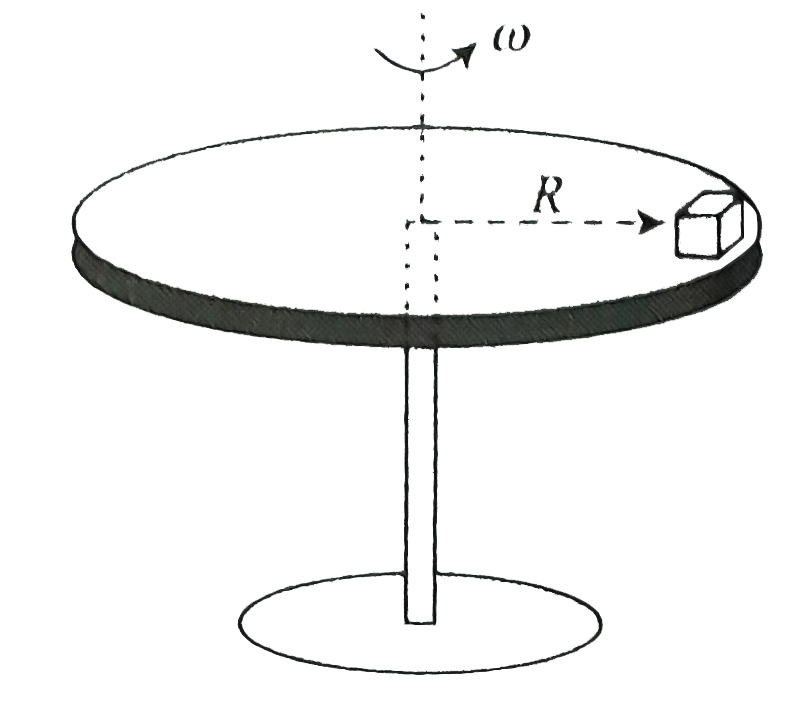
View SolutionA block of mass m is kept on the edge of a horizontal turn table of radius R which is rotating with constant angular verticle ω (along with the block ) about its axis . If coefficient of friction is μ, find the friction force between block and table.
View SolutionA block of mass m is connected with another block of mass 2m kept on a rough horizontal table by means of an ideal spring of spring constant K and a massless string as shown in the figure. The minimum coefficient of friction between the block of mass 2m and the table so that the block does not slide, when block of mass m is suddenly released, is
View SolutionA block of mass m moving at a speed v compresses a spring throgh a distance x before its speed is halved. Find the spring constant of the spring.
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionIn the position shown in figure, the spring is at its natural length. The block of mass m is given a velocity v0 towards the vertical support at t=0. The coefficient of friction between the block and the surface is given by μ=αx, where α is a positive constant and x is the position of the block from its starting position. The block comes to rest for the first time at x, which is
View SolutionA block of mass m lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant k) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched (x=0). When a constant horizontal force →F in the positive direction of the x−axis is applied to it, a plot of the resulting kinetic energy of the block versus its position x is shown in figure. What is the magnitude of →F ?
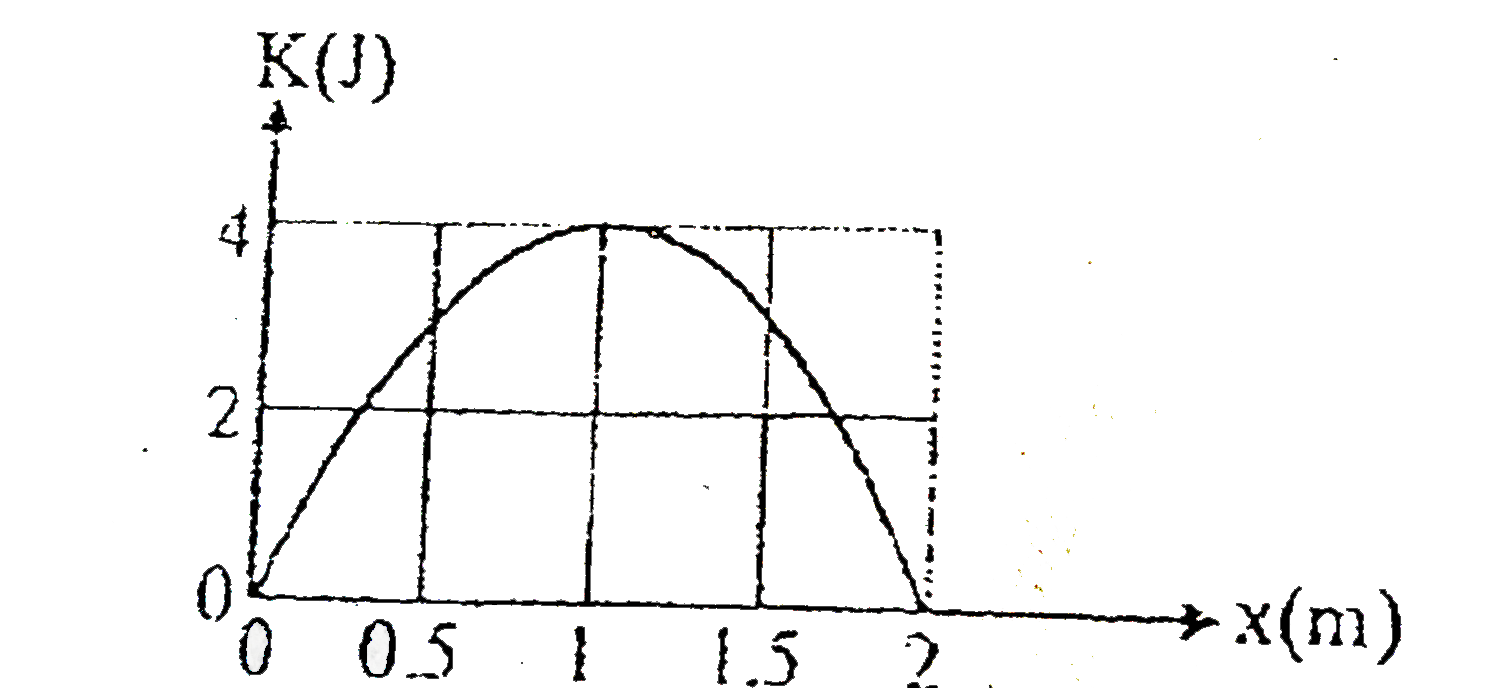
View Solution
