In the position shown in figure, the spring is at its natural length. The block of mass m is given a velocity v0 towards the vertical support at t=0. The coefficient of friction between the block and the surface is given by μ=αx, where α is a positive constant and x is the position of the block from its starting position. The block comes to rest for the first time at x, which is
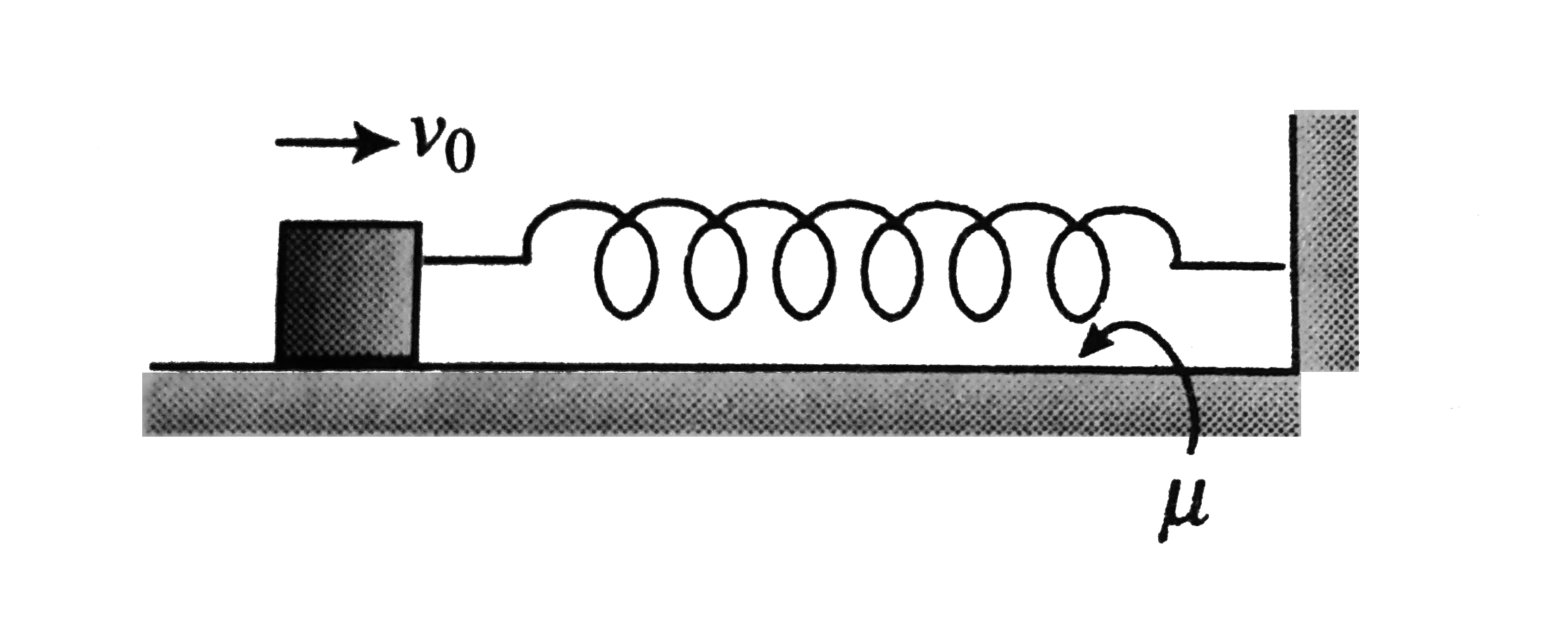
(a) v0√mk+αmg
(b) v0√mk
(c) v0√mαg
(d) None of these
The correct Answer is:A
According to the work-energy theorem,
12mv20=mgαx∫0dx+12kx2
Solving we get, x=v0√mk+αmg
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A block of mass m is slowly pulled along a curved surface from position 1 and 2. If the coefficient of kinetic friction between the block and surface is μ, find the work done by the applied force.

View SolutionA small block of mass 1kg is at rest on a parabolic surface given by y=x2. The coefficient of friction between the block and the surface is enough to prevent slipping.If position of block on surface is( 2m, 4m) then the normal force then the surface exerts at this position is
_PHY_E05_036_Q001.png)
View SolutionA small block of mass 1 kg is at rest on a parabolic surface given by y=x2. The coefficient of friction between the block and the surface is enough to prevent slipping. If position of block on surface is (2 m, 4 m), then the normal force that the surface exerts at this position is
_PHY_E05_190_Q04.png)
View SolutionA block of mass m is placed on a vertical fixed circular track and then it is given velocity v along the track at position A on track. The coefficient of friction between the block and the track varies with the angle θ . If the block moves on track with constant speed then the coefficient of friction is
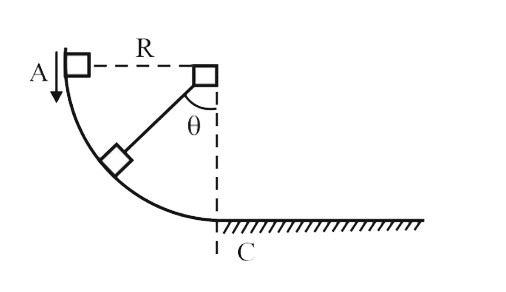
View SolutionA block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
View SolutionA block of mass 4 kg is kept over a rough horizontal surface. The coefficient of friction between the block and the surface is 0.1 At, t=0, (3ˆi)(ms) velocity is imported to the block simultaneously (−2ˆi)N force starts acting on it. Its displacement in first 5s is
View SolutionIn the system as shown in figure, the blocks have masses m1 and m2, the spring constant is k, coefficient of friction between the block of mass m1 and the surface is μ. The system is released with zero initial speed from the position where the spring is in its natural length.

View Solution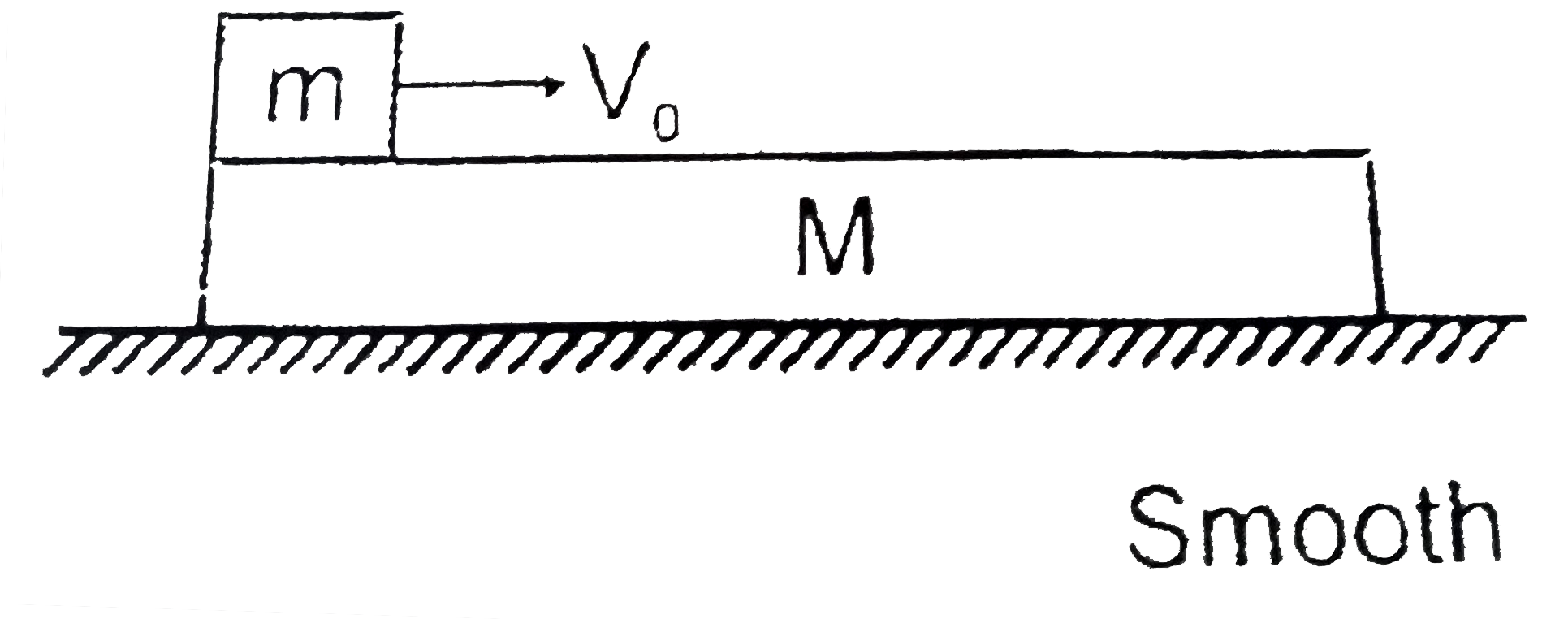
The block of mass m is kept on plank of mass M. The block is given velocity V0 as shown. The coefficient of friction between the block of mass m and plank of mass M is μ and its value is such that block becomes stationary with respect to plank before it reaches the other end. Then:
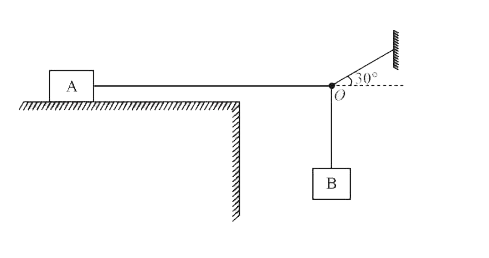
View SolutionThe block A in the given figure is of mass 10√3 kg The coefficient of friction between the block and the surface on which it rests is 0.5. Find maximum mass of block B possible such that the system will be in equilibrium is.
View SolutionOn a stationary block of mass 2kg a horizontal forces F starts acting at t=0 whose veriation with time is shown in figure .The coefficient of friction between the block and ground is 0.5 New answer the following question
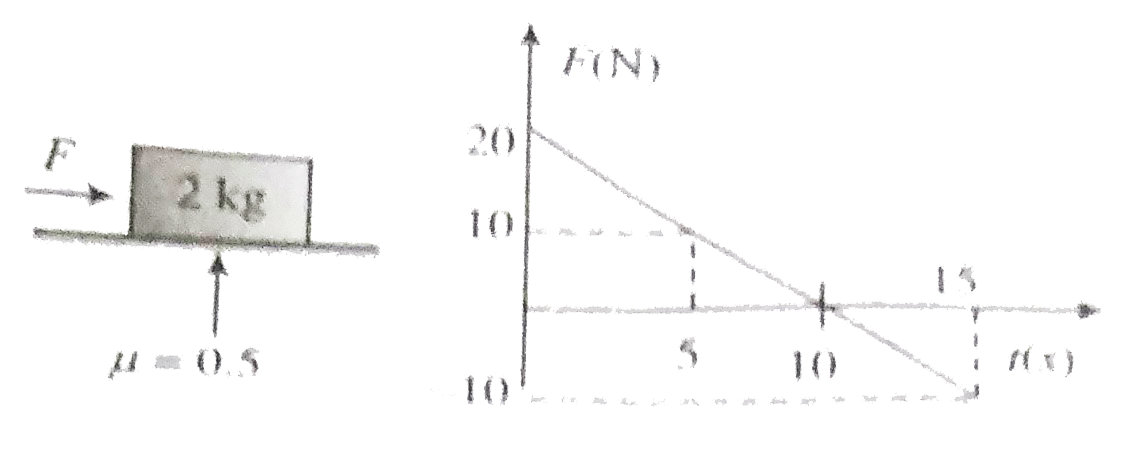
Find the velocity of the block when for the firsst time its acceleration become zero
View Solution
