A person pulls a bucket of water from a well of depth h. if the mass of uniform rope is and that of the bucket full 0f water is M, then work done by the person is.
(M+m2)gh
1/2 (M + m)gh
(M+m)gh
(M2+m)gh
The correct Answer is:A
To solve the problem of calculating the work done by a person pulling a bucket of water from a well of depth H using a rope of mass m and a bucket of mass M, we can follow these steps:
Step 1: Understand the System
We have a rope of mass m and a bucket of mass M at the bottom of a well of depth H. When the bucket is pulled up, both the bucket and the rope will gain potential energy.
Step 2: Calculate the Potential Energy Gained by the Bucket
The potential energy gained by the bucket when it is lifted to height H is given by the formula:
PEbucket=M⋅g⋅H
where g is the acceleration due to gravity.
Step 3: Calculate the Potential Energy Gained by the Rope
The rope is uniform, and its center of mass is located at its midpoint. As the entire rope is lifted, the center of mass of the rope will rise by H2. Therefore, the potential energy gained by the rope is:
PErope=m⋅g⋅H2
Step 4: Calculate the Total Work Done
The total work done by the person in pulling the bucket and the rope is the sum of the potential energies gained by both:
W=PEbucket+PErope
Substituting the expressions we found:
W=M⋅g⋅H+m⋅g⋅H2
Step 5: Factor Out Common Terms
We can factor out gH from the total work done:
W=gH(M+m2)
Final Answer
Thus, the work done by the person in pulling the bucket of water from the well is:
W=gH(M+m2)
We have a rope of mass m and a bucket of mass M at the bottom of a well of depth H. When the bucket is pulled up, both the bucket and the rope will gain potential energy.
The potential energy gained by the bucket when it is lifted to height H is given by the formula:
PEbucket=M⋅g⋅H
where g is the acceleration due to gravity.
The rope is uniform, and its center of mass is located at its midpoint. As the entire rope is lifted, the center of mass of the rope will rise by H2. Therefore, the potential energy gained by the rope is:
PErope=m⋅g⋅H2
The total work done by the person in pulling the bucket and the rope is the sum of the potential energies gained by both:
W=PEbucket+PErope
Substituting the expressions we found:
W=M⋅g⋅H+m⋅g⋅H2
We can factor out gH from the total work done:
W=gH(M+m2)
Thus, the work done by the person in pulling the bucket of water from the well is:
W=gH(M+m2)
Topper's Solved these Questions
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 1 subjective
Explore 27 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 2 Objective
Explore 30 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 1 Assertion And Reason
Explore 12 Videos
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Integer Type Question
Explore 11 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
A man pulls a bucket of water from a depth of h from a well. If the mass of the rope and that of bucket full of water are m and M respectively, the work done by the man is :
View SolutionA man slowly pulls a bucket of water from a well of depth h=20m. The mass of the uniform rope and bucket full of water are m=200g and M 19.9kg, respectively. Find the work done (∈kJ) by the mean.
View SolutionA man pulls out a block of mass m from the depth d with help of a light string. If acceleration of the block is g2 then the work done by the string on the block will be
View SolutionA person brings a mass of 1 kg infinity to a point A. Initially the mass was at rest but it moves at a speed of 2ms−1 as it reached A. The work done by the person on the mass is −3J. The potential at A is
View SolutionA bucket water filled upto a height = 15 cm. The bucket is tied to a rope which is passed over a frictionless light pulley and the other end of the rope is tied to a weight of mass which is half of that of the (bucket + water). The water pressure above atmospheric pressure at the bottom is
View SolutionA person holds a bucket of weight 60N . He walks 7m along the horizontal path and then climbs up a vertical distance of 5m. The work done by the man is
View SolutionA person brings a mass of 1 kg from infinity to a point . Initally the mass was at rest but it moves at a speed of 2 ms−1 as it reaches A. The work done by the person on the mass is -3J. The potential at A is
View SolutionFind the net downward thrust on the clined surface of a bucket full of water of height h and radii a and b.
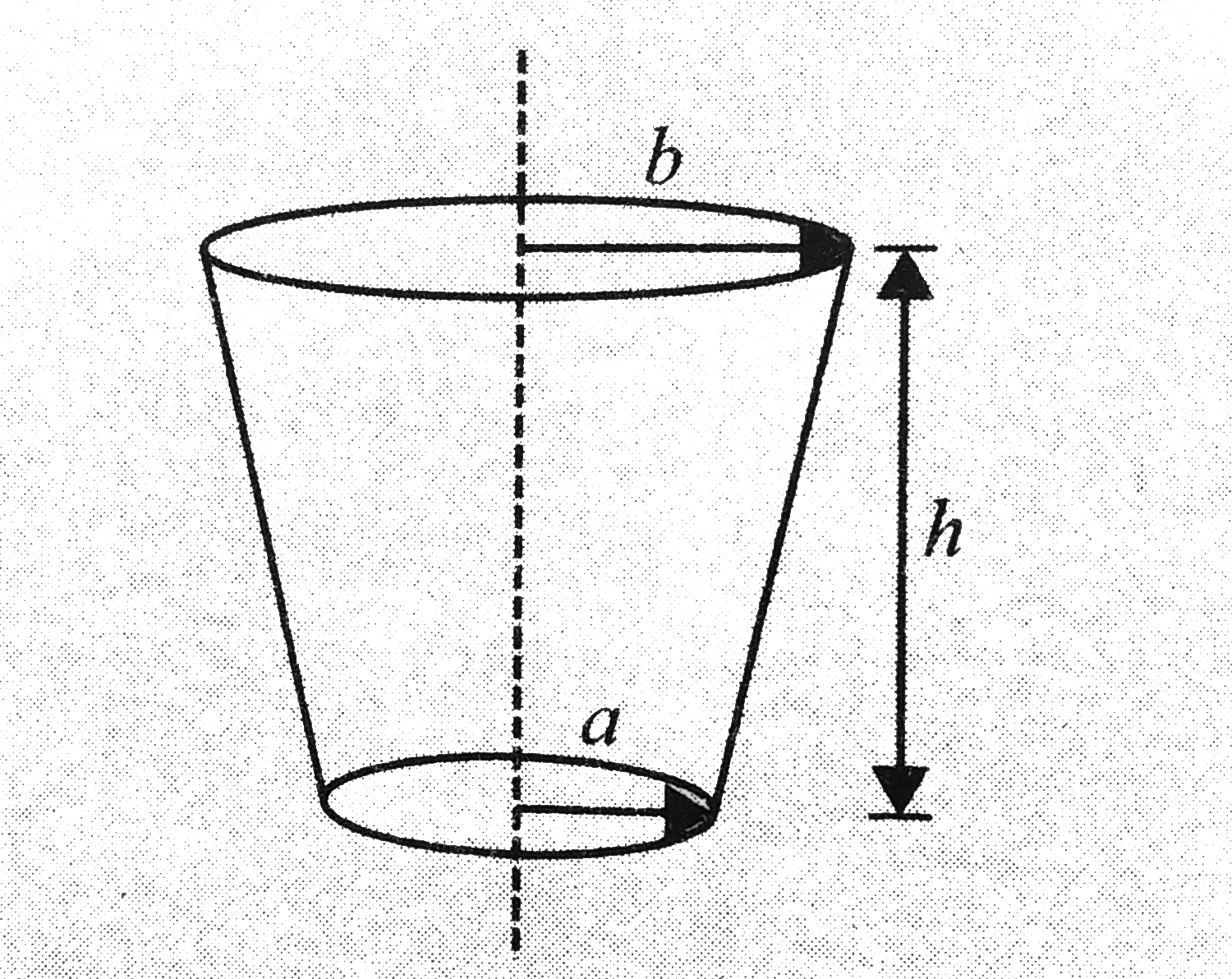
View SolutionA person brings a mass of 1kg from infinity to a point A. Initially the mass was at rest but it moves with a speed of 2m/s as it reaches A. The work done by the person on a mass is −3J. The potential of A is:
View SolutionA person brings a mass of 1kg from infinity to a point A. Initially the mass was at rest but it moves with a speed of 2m/s as it reaches A. The work done by the person on a mass is −3J. The potential of A is:
View Solution