A block rests on a rough plane whose inclination to the horizontal can be varied. Which of the following graphs indicates how the friction force between the block and the plane varies as is increased?
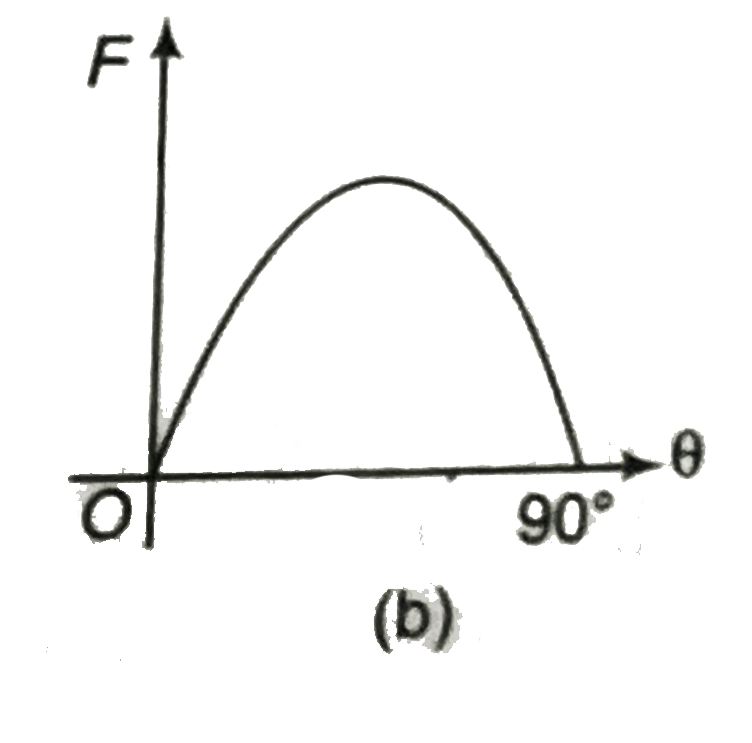
The correct Answer is:B
To solve the problem, we need to analyze how the friction force F between the block and the inclined plane varies as the angle θ is increased.
1. Understanding the Forces: When a block is resting on an inclined plane, the forces acting on it include gravitational force, normal force, and frictional force. The gravitational force can be resolved into two components: one parallel to the incline (which tries to slide the block down) and one perpendicular to the incline (which affects the normal force).
2. Static Friction: For small angles θ (where θ<α, with α being the angle of repose), the block does not slide. The frictional force F will balance the component of the gravitational force acting down the slope. This can be expressed as:
F=mgsinθ
Here, m is the mass of the block and g is the acceleration due to gravity.
3. Behavior as θ Increases: As θ increases, sinθ also increases, which means the frictional force F increases as long as the block remains stationary.
4. Angle of Repose: When θ reaches the angle of repose α, the block is on the verge of sliding. At this point, the maximum static friction force is equal to:
Fmax=μsmgcosθ
where μs is the coefficient of static friction.
5. Transition to Kinetic Friction: Once θ exceeds α, the block starts to slide down the plane. The frictional force now becomes kinetic friction, which is given by:
F=μkmgcosθ
where μk is the coefficient of kinetic friction.
6. Graphical Representation:
- For θ<α, F increases with sinθ.
- For θ≥α, F decreases with cosθ.
7. Conclusion: The graph that represents this behavior will show an increase in friction force F as θ increases until it reaches a maximum at θ=α, and then it will decrease as θ continues to increase beyond α.
Final Answer:
The correct graph indicates that the friction force F increases with θ until it reaches the angle of repose and then decreases as θ continues to increase.
F=mgsinθ
Here, m is the mass of the block and g is the acceleration due to gravity.
Fmax=μsmgcosθ
where μs is the coefficient of static friction.
F=μkmgcosθ
where μk is the coefficient of kinetic friction.
- For θ<α, F increases with sinθ.
- For θ≥α, F decreases with cosθ.
The correct graph indicates that the friction force F increases with θ until it reaches the angle of repose and then decreases as θ continues to increase.
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Objective Question
Explore 32 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Comprehension
Explore 9 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Assertion And Reason
Explore 28 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A body is placed on a rough inclined plane of inclination θ. As the angle θ is the increased from 0∘ to 90∘, the contact force between the block and the plane
View SolutionA body is placed on a rough inclined plane of inclination θ. As the angle θ is the increased from 0∘ to 90∘, the normal force between the block and the plane is,
View Solution
Knowledge Check
A block of mass 3 kg rests on a rough inclined plane making an angle of 30∘. With the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8 NB0.7×9.8×√3 NC9.8×√3 ND0.7×9.8 NA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3N
A block of weight 1 N rests on a inclined plane of inclination θ with the horizontal. The coefficient of friction between the block and the inclined plane is μ. The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View Solution