For a moving particle, which of the following options may be correct? Here, Vav is average velocity and vav the average speed.
|Vav|<vav
|Vav|>vav
Vav=0 but vav≠0
Vav≠0butvav=0
The correct Answer is:A, C
To solve the question regarding the relationship between average velocity (Vav) and average speed (vav) for a moving particle, we can follow these steps:
1. Understand Definitions:
- Average speed (vav) is defined as the total distance traveled divided by the total time taken:
vav=Total DistanceTotal Time
- Average velocity (Vav) is defined as the total displacement divided by the total time taken:
Vav=Total DisplacementTotal Time
2. Relationship Between Distance and Displacement:
- It is important to note that the total distance traveled is always greater than or equal to the magnitude of the total displacement. This is because displacement is a vector quantity that considers direction, while distance is a scalar quantity that does not:
Total Distance≥|Total Displacement|
3. Implications for Average Speed and Average Velocity:
- From the relationship established in the previous step, we can conclude that:
vav≥|Vav|
- This means that the average speed is always greater than or equal to the magnitude of the average velocity.
4. Consider Special Cases:
- If the average velocity (Vav) is zero, it implies that the total displacement is zero. However, the average speed (vav) can still be greater than zero if the particle has traveled a distance but returned to its starting point.
- Conversely, if the average speed (vav) is zero, it means the particle has not moved at all, which implies that the average velocity (Vav) must also be zero.
5. Conclusion:
- Therefore, the correct statements regarding average velocity and average speed are:
- Average speed is always greater than or equal to the magnitude of average velocity.
- Average velocity can be zero while average speed is not zero, but not the other way around.
Final Answer:
- Option 1: vav≥|Vav| is correct.
- Option 3: Vav=0 does not imply vav=0 is also correct.
- Average speed (vav) is defined as the total distance traveled divided by the total time taken:
vav=Total DistanceTotal Time
- Average velocity (Vav) is defined as the total displacement divided by the total time taken:
Vav=Total DisplacementTotal Time
- It is important to note that the total distance traveled is always greater than or equal to the magnitude of the total displacement. This is because displacement is a vector quantity that considers direction, while distance is a scalar quantity that does not:
Total Distance≥|Total Displacement|
- From the relationship established in the previous step, we can conclude that:
vav≥|Vav|
- This means that the average speed is always greater than or equal to the magnitude of the average velocity.
- If the average velocity (Vav) is zero, it implies that the total displacement is zero. However, the average speed (vav) can still be greater than zero if the particle has traveled a distance but returned to its starting point.
- Conversely, if the average speed (vav) is zero, it means the particle has not moved at all, which implies that the average velocity (Vav) must also be zero.
- Therefore, the correct statements regarding average velocity and average speed are:
- Average speed is always greater than or equal to the magnitude of average velocity.
- Average velocity can be zero while average speed is not zero, but not the other way around.
- Option 1: vav≥|Vav| is correct.
- Option 3: Vav=0 does not imply vav=0 is also correct.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - More Than One Correct
6 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Objective
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Knowledge Check
For any arbitrary motion in space, which of the following relations are true?
a) vaverage=(1/2)(v(t1+v(t2)
b) vaverage=[r(t2)−rt1t2−t1
v(t)=v(0)+at
d) aaverage=[v(t2)−vt1t2−t1
The average stands for average of the quantity over time interval t1 to t_(2)A→vaverage=12[→v(t1)+→v(t2)]B→vaverage=→r(t2)−→r(t1)t2−t1C→v(t)=→v(0)+→atD→r(t)=→r(0)+→v(0)t+12→at2Which of the following characters does not fit for Aves ?
ASkin is dry, without glands except oil/preen glands at the base of tailBAlimentary canal has 2 additional chambers, crop and gizzardCHind limbs are modified for walking, swimming or clasping. Forelimbs are modified into wings.DBeak has teethWhich of the following statements is incorrect? (i) Average velocity is path length divided by time interval.
(ii) In general, speed is greater than the magnitude of the velocity.
(iii) A particle moving in a given direction with a non-zero velocity can have zero speed. (iv) The magnitude of average velocity is the average speed.A(ii) and (iii)B(ii) and (iv)C(i), (iii) and (iv)DAll four
A particle obeys the following v - t graph as shown. The average velocity over 30 s is

View SolutionDistinguish between average speed and average velocity.
View SolutionThe correct relation between tav=average life and t1/2= half life for a radioactive nuclei.
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. In the time interval from t=0 to t=14s, find
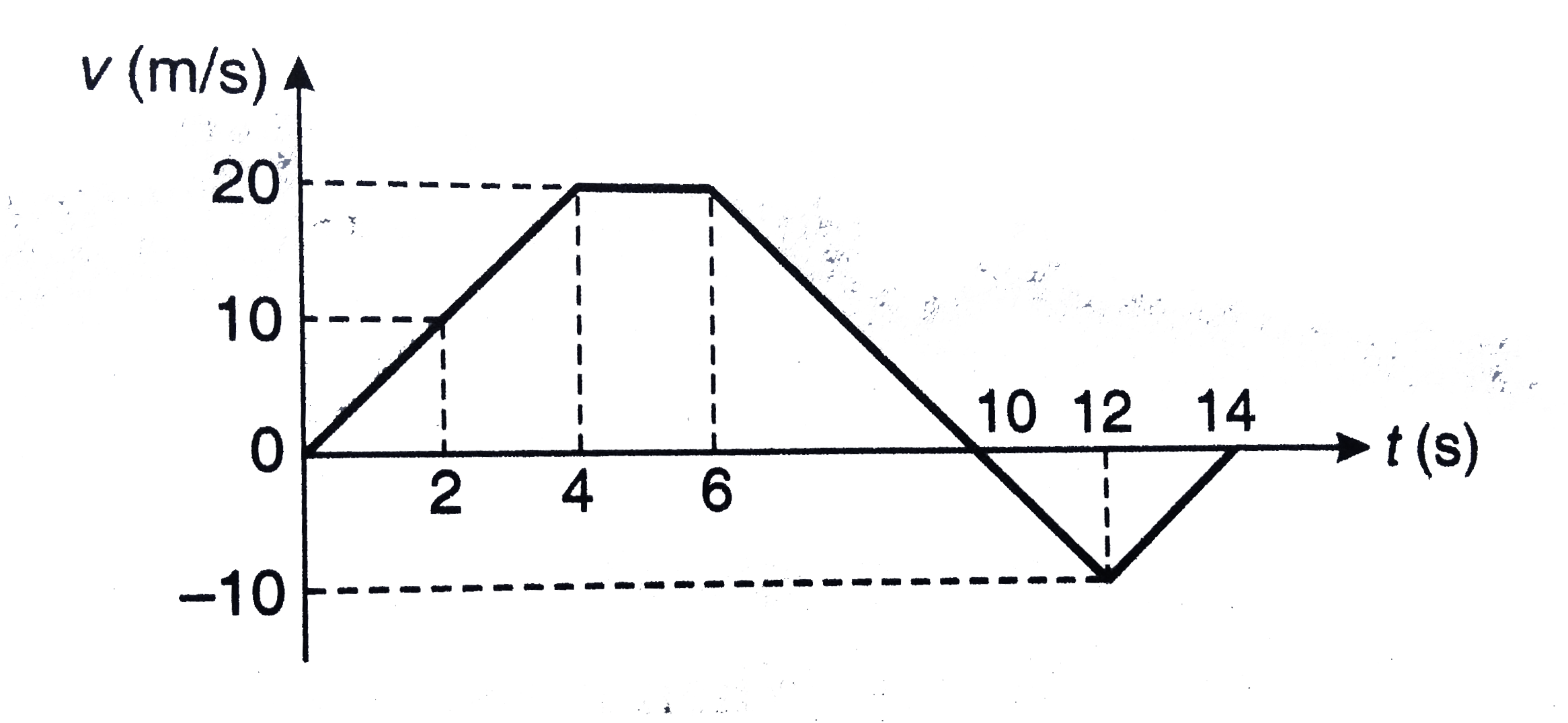
(a) average velocity and
(b) average speed of the particle.
View SolutionThe v-t graph for a particle moving along x-axis is shown in the figure, find
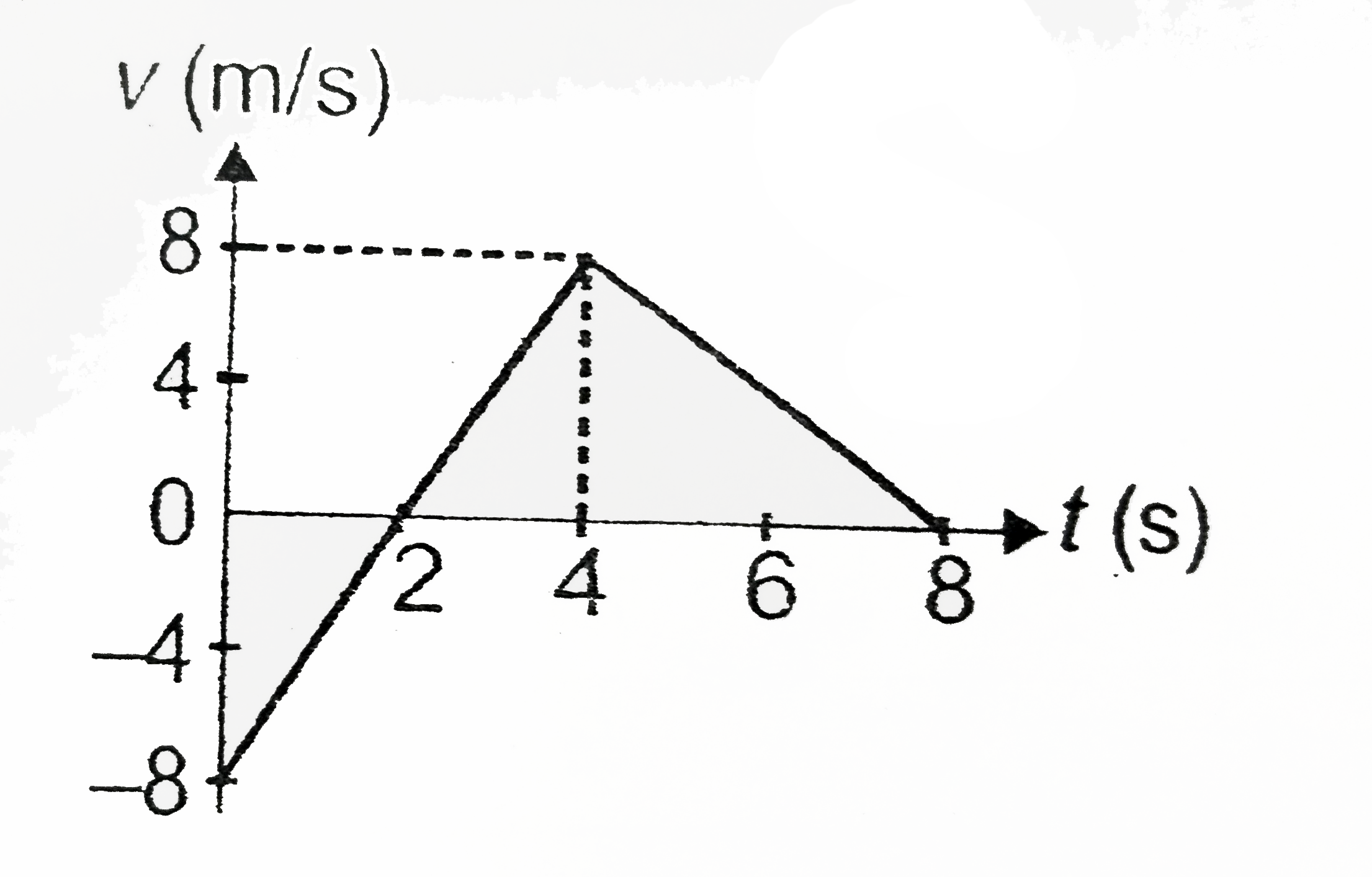
(a) Average velocity in the interval 0 to 8 s.
(b) Average speed in the interval 0 to 8 s.
(c) Average acceleration in the interval 0 to 4 s.
(d) Instantaneous acceleration at t = 2.5 s.
View Solution
